Các vị trí quan trọng trong dao động điều hòa , các khoảng thời gian đặc biệt cần ghi nhớ

Dạng toán về các vị trí quan tr ọng trong dao động điều hòa , các khoảng thời gian đặc biệt cần ghi nhớ
A- Lý thuyết cần nhớ .
Phần 1 : kiến thức về vòng tròn liên hệ giữa chuyển động tròn và dao động điều hòa .

1) Nhắc lại kiến thức về chuyển động tròn.
a) chuyển động tròn : là chuyển động có quỹ đạo là một đường tròn.
b) tần số góc ($\omega $) : trong chuyển động tròn là đại lượng đo bằng góc mà bán kính OM quét được trong một đơn vị thời gian , và là một đại lượng không đổi
Ta có : $\omega =\frac{\Delta \alpha }{\Delta t}$ ( rad/s)
với $\Delta \alpha $ : là góc quét được trong khoảng thời gian $\Delta t$ .
2) Liên hệ giữa chuyển động tròn và dao động điều hòa .
- Xét trong hệ trục tọa độ (Oxy) một đường tròn tâm O bán kính R
- và một vật chuyển động tròn đều từ vị trí ${{M}_{o}}$ với tần số góc $\omega $ và đi ngược chiều kim đồng hồ 

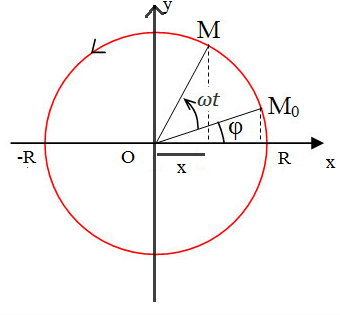
Ta thấy : +) từ ban đầu đến thời điểm t vật đã quét thêm được một góc \[(\omega t+\varphi )\]

               +) tại điểm M vật có vị trí là x , với $x=R.\cos (\omega t+\varphi )$ $\to $ đây là dạng phương trình li độ của dao động điều hòa
$\to $ ta có thể nói dao động điều hòa chính là hình chiếu của chuyển động tròn đều theo phương ngang Ox ( với  R ~ A )
Note : - coi chiều (+) là chiều trùng với phương Ox
           $\to $ phần phía trên trục Oy thì $\varphi >o,v<0$ (vận tốc âm vì chuyển động hình chiếu ngược chiều +)
           $\to $ phần phía dưới trục Oy thì $\varphi <0,v>0$ (vận tốc dương do chuyển động hình chiếu cùng chiều +)
3) Áp dụng vòng tròn liên hệ vào giải quyết các bài toán
- Bài toán liên quan đến thời gian (đi từ vị trí x1 đến vị trí x2)
Cách 1: sử dụng vòng tròn liên hệ ( đây là cách thông dụng các bạn chú ý để hiểu thật kĩ nha ) .
- phương pháp : xác định góc quét $\alpha =\omega t$
Cách 2 : sử dụng phương trình lượng giác .

phương pháp : dựa vào phương trình li độ để tìm ra thời gian t
(*) mình sẽ giải thích kĩ cả 2 cách trong từng ví dụ :
Phần 2 : Một số vị trí và các khoảng thời gian quan trọng cần ghi nhớ .
1) các vị trí quan trọng
- Các vị trí quan trọng thường gặp là : $\pm A,\pm \frac{A\sqrt{3}}{2},\pm \frac{A\sqrt{2}}{2},\pm \frac{A}{2}$ ,….
Note : các bạn sẽ hay gặp những vị trí này ở các phần dao động chú ý nhé !

2) Các khoảng thời gian quan trọng .( nên nhớ )
a) thời gian đi trong một chu kì = T
b) thời gian đi từ -A đến A = $\frac{T}{2}$ ( một nửa chu kì ).
c) thời gian đi từ O ( VTCB) đến $\pm A$  ( biên) = $\frac{T}{4}$
 +) chứng minh : B1) xác định góc quét

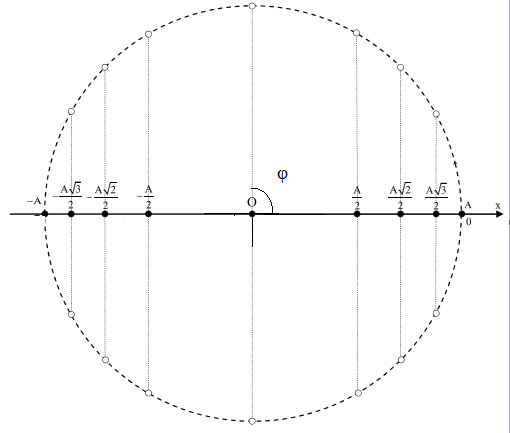
+) Ta thấy : từ VTCB đến biên A góc quét được là góc $\varphi =\frac{\pi }{2}$
$\to $ Từ công thức liên hệ ta có: $\omega =\frac{\Delta \alpha }{\Delta t}\to \Delta t=\frac{\Delta \alpha }{\omega }$ ( với $\Delta \alpha $ là góc quét được ($\varphi $) ) $\to $ $\Delta t=\frac{\pi /2}{\omega }$ mà $\omega =\frac{2\pi }{T}$ $\to $  $\Delta t=\frac{T}{4}$

c) thời gian đi từ O ( VTCB) đến $\pm \frac{A}{2}$ = $\frac{T}{12}$
+) chứng minh :
B1) xác định góc quét :

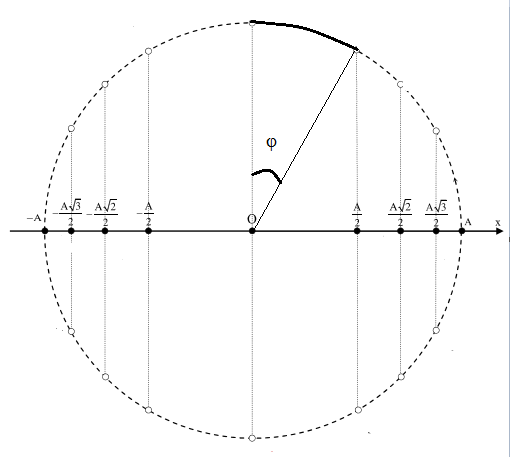
Ta thấy : khi vật đi từ O ( VTCB) đến vị trí $\frac{A}{2}$ góc quét được là $\varphi =\frac{\pi }{6}\left( \sin (\varphi )=\frac{A/2}{A}\to \varphi =\frac{\pi }{6} \right)$
$\to $ Từ công thức liên hệ ta có: $\omega =\frac{\Delta \alpha }{\Delta t}\to \Delta t=\frac{\Delta \alpha }{\omega }$ ( với $\Delta \alpha $ là góc quét được ($\varphi $) ) $\to $ $\Delta t=\frac{\pi /6}{\omega }$ mà $\omega =\frac{2\pi }{T}$ $\to $  $\Delta t=\frac{T}{12}$

d) thời gian đi từ O ( VTCB) đến $\pm \frac{A}{\sqrt{2}}$ = $\frac{T}{8}$
e) thời gian đi từ O (VTCB) đến $\pm \frac{A\sqrt{3}}{2}$ = $\frac{T}{6}$
(*) các bạn dựa vào hướng dẫn của mình rồi chứng minh nha .
g) thời gian đi từ vị trí khác gốc tọa độ .
+) Phương pháp : các bạn cộng hoặc trừ các khoảng thời gian đặc biệt mình làm rõ ở trên .
VD : +) ${{t}_{(A\to \frac{A}{2})}}={{t}_{\left( O\to A \right)}}-{{t}_{\left( O\to \frac{A}{2} \right)}}=\frac{T}{4}-\frac{T}{12}=\frac{T}{6}$ .
         +) ${{t}_{\left( \frac{A}{2}\to \frac{A\sqrt{3}}{2} \right)}}={{t}_{\left( O\to \frac{A\sqrt{3}}{2} \right)}}-{{t}_{\left( O\to \frac{A}{2} \right)}}=\frac{T}{6}-\frac{T}{12}=\frac{T}{12}$ .
         +)${{t}_{\left( \frac{A}{\sqrt{2}}\to \frac{A}{2} \right)}}={{t}_{\left( O\to \frac{A}{2} \right)}}-{{t}_{\left( O\to \frac{A}{\sqrt{2}} \right)}}=\frac{T}{8}-\frac{T}{12}=\frac{T}{24}$
B) Một số dạng bài tập .
Câu 1 : Một vật dao động điều hòa với phương trình li độ $x=5.\cos (10\pi t)$cm. Tính thời gian ngắn nhất vật đi từ VTCB đến vị trí $x=2,5cm$???
A) 0,0083
B) 0,00416
C) 0,0125
D) 0,025
Đáp án : A ( cụm từ ‘ ngắn nhất’ nghĩa là thời gian vật đi thẳng từ vị trí cân bằng đến vị trí $\frac{A}{2}$ . Ta sử dụng khoảng thời gian đặc biệt ${{t}_{\left( O\to \frac{A}{2} \right)}}=\frac{T}{12}$)

Câu 2 : Một chất điểm dao động điều hòa với biên độ A= 8 cm , tốc độ góc 10(rad/s) , khoảng thời gian ngắn nhất vật đi từ vị trí có li độ +3,5 đến VTCB là :
A) 0,07(s)
B) 0,04528(s)
C) 0,05235(s)
D) 0,00109(s)
Đáp án : B  ( *) ta thấy vị trí li độ khác các vị trí đặc biệt nên chúng ta sẽ giải quyết bài toán theo cách làm bình thường ..
Phương pháp : ( tìm góc quét )
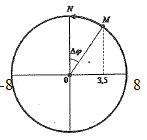từ vòng tròn liên hệ ta thấy vật chuyển động từ M đến N
chính là khoảng thời gian ngắn nhất vật đi từ li độ 3,5 đến VTCB

Câu 3 : Một vật dao động điều hòa , biết khoảng thời gian ngắn nhất vật đi từ vị trí có li độ A/2 đến vị trí có li độ A là 0,2 (s) . Tính tần số của dao động?
A) 1,2 Hz
B) 5,23 Hz
C) 5/6 Hz
D) 0,2 Hz
Đáp án : C (*)  đây là các khoảng thời gian đặc biệt nhưng không xuất phát từ VTCB nên ta sử dụng phương pháp cộng hoặc trừ các khoảng thời gian đặc biệt
Ta có : +) ${{t}_{(A\to \frac{A}{2})}}={{t}_{\left( O\to A \right)}}-{{t}_{\left( O\to \frac{A}{2} \right)}}=\frac{T}{4}-\frac{T}{12}=\frac{T}{6}$
$\to \frac{T}{6}=0,2\to T=1,2\to f=\frac{1}{T}=\frac{5}{6}(Hz)\to C$ !!!

Câu 4 : Một vật dao động điều hòa với chu kì T=1s , biên độ A=4cm .Khoảng thời gian trong nửa chu kì để vật cách VTCB một đoạn nhỏ hơn 2cm là ?
A)1/8(s)
B)1/24(s)
C)1/12(s)
D)1/6 (s)
Đáp án : D (*) trong một nửa chu kì sẽ có 2 khoảng thời gian để vật cách VTCB một đoạn nhỏ hơn 2cm
Ta thấy đây là bài toán có vị trí đặc biệt nên ta sẽ sử dụng các khoảng thời gian đặc biệt ( bài toán ở đây là vị trí đặc biệt A/2) .
$\to $ ${{t}_{\left( O\to \frac{A}{2} \right)}}=\frac{T}{12}$ $\to $ $\Delta t=2t$ ( có 2 khoảng thời gian ) $\to $ $\Delta t=\frac{T}{6}=\frac{1}{6}(s)$ $\to D$!!!
Câu 5 : Một chất điểm dao động điều hòa với chu kỳ T . Khoảng thời gian trong một chu kì để vật có tốc độ lớn hơn 0,5 lần tốc độ cực đại là :
A) T/3
B) 2T/3
C) T/6
D) T/2
Đáp án : B (*)  đây là một bài toán có hơi chút phức tạp do người ra đề đã lồng thêm dạng toán khác vào , để giải quyết bài toán chúng ta sẽ giải từng bài toán nhỏ trước
- ‘tốc độ lớn hơn 0,5 lần tốc độ cực đại’ $\to v>\frac{{{v}_{_{\max }}}}{2}$ $\to v>\frac{\omega A}{2}$
- sử dụng công thức độc lập ta có : $\to $ ${{A}^{2}}={{x}^{2}}+\frac{{{v}^{2}}}{{{\omega }^{2}}}$ $\to x=\frac{A\sqrt{3}}{2}$ .
- bài toán trở lại giống câu 4
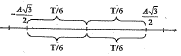( càng gần VTCB thì vận tốc càng lớn )
$\to 4t=4.\frac{T}{6}=\frac{2T}{3}\to B$ ( vì trong 1 chu kì có 4 khoảng thời gian thỏa mãn đề bài)
C) Các bài tập tự luyện năng cao kĩ năng .
Câu 1 : Một vật dao động điều hòa có phương trình li độ là : $x=8.\cos (7\pi t+\frac{\pi }{6})$ . Khoảng thời gian tối thiểu vật đi từ vị trí có li độ $4\sqrt{2}$ đến vị trí có li độ $-4\sqrt{3}$ là ???
A) 1/24 (s)
B) 5/12(s)
C) 1/6 (s)

D) 1/12(s).
Câu 2 : Một vật dao động điều hòa với chu kì T và biên độ A . Thời gian ngắn nhất vật đi từ vị trí vật có li độ cực đại về vị trí li độ bằng một nửa li độ cực đại mà vecto vận tốc cùng hướng với trục tọa độ là ???
A) 5T/6
B) T/12
C) T/3
D) T/8
- hình vẽ gợi ý :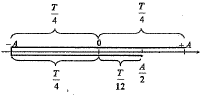
Câu 3 : Một chất điểm dao động điều hòa với chu kì T. Trong khoảng thời gian ngắn nhất khi đi từ vị trí biên có li độ x = A đến vị trí x = ‒A/2, chất điểm có tốc độ trung bình là???
A) 4,5A/T
B) 6A/T
C) 9A/T
D) 10T/11
Note : Tốc độ trung bình được tính theo công thức : $\left| v \right|=\frac{\Delta S}{\Delta t}$ .
Câu 4 : Một chất điểm dao động điều hòa với chu kì T. Gọi vtb là tốc

độ trung bình của chất điểm trong một chu kì, v là tốc độ tức thời của chất điểm.Trong một chu kì, khoảng thời gian mà v ≥ 0,25pvtb là:
A) T/3
B) 2T/3
C) T/6
D) T/3 .
- Gợi ý : Xét ${{v}_{1}}=0,25\pi {{v}_{tb}}({{v}_{tb(1T)}}=\frac{4A}{T}=4A.\frac{\omega }{2\pi })$ .
Câu 5: Một vật nhỏ dao động điều hòa theo phương trình x =Acos4pt (t tính bằng s). Tính từ t = 0 khoảng thời gian ngắn nhất để gia tốc của vật có độ lớn bằng một nửa độ lớn gia tốc cực đại là???
A) 0.083 (s)
B) 0,104 (s)
C) 0,167 (s)
D) 0,125 (s)
Câu 6 : Một vật nhỏ dao động điều hòa theo một quỹ đạo thẳng dài 14

cm với chu kì 1 s. Thời gian bắt đầu từ thời điểm vật qua vị trí có li độ 3,5 cm theo chiều dương đến khi gia tốc của vật đạt giá trị cực tiểu lần thứ hai là bao nhiêu ???
A) 1/6 (s)
B) 7/6 (s)
C) 5/6 (s)

D) 1/3 (s)
Note : quỹ đạo dài = 2A.
Câu 7 : Một vật dao động điều hòa thời gian ngắn nhất vật đi từ vị trí $x=+A$ đến vị trí $x=\frac{A}{3}$ là 0,1 s . Tính chu kì dao động của vật ???
A) 1,85 (s)
B) 1,2 (s)
C) 0,51 (s)
D) 0,4 (s)
Câu 8 : Một vật dao động điều hòa với chu kì 1s và biên độ 4,5 cm . Khoảng thời gian trong 1 chu kì để vật cách vị trí cân bằng 1 khoảng nhỏ hơn 2cm là ???
A) 0,29 (s)
B) 16,8 (s)
C) 0,71 (s)
D) 0,15 (s) 
- Gợi ý : tìm góc quét .
Câu 9 : Một vật nhỏ dao động điều hòa với biên độ 8 cm. Biết trong một chu kì thời gian để vật nhỏ có độ lớn vận tốc không vượt quá 16 cm là T/3 . Tần số góc của dao động là ???
A) 4 rad/s
B) 3 rad/s
C) 2 rad/s
D) 5 rad/s

Câu 10 :  Một chất điểm đang dao động điều hoà trên một đoạn thẳng. Trên đoạn thẳng đó có bảy điểm theo đúng thứ tự M₁, M₂, M₃, M₄, M₅, M₆ và M₇ với M₄ là vị trí cân bằng. Biết cứ 0,05 s thì chất điểm lại đi qua các điểm M₁, M₂, M₃, M₄, M₅, M₆ và M₇. Tốc độ của nó lúc đi qua điểm M₃ là 20π cm/s. Biên độ A bằng ???
A) 4 cm
B) 6 cm
C) 12 cm
D) $4\sqrt{3}$ cm .

Bài viết gợi ý: