I.Lý thuyết:
Bước 1. Lập phương trình hoặc hệ phương trình
+ Chọn ẩn, đơn vị cho ẩn, điều kiện thích hợp cho ẩn
+ Biểu đạt các đại lượng khác theo ẩn (chú ý thống nhất đơn vị)
+ Dựa vào dữ kiện, điều kiện của bài toán để lập phương trình hoặc hệ phương trình
Bước 2. Giải phương trình hoặc hệ phương trình
Bước 3. Nhận định, so sánh kết quả bài toán, tìm kết quả thích hợp, trả lời (bằng câu viết) nêu rõ đơn vị của đáp số
Các dạng toán cơ bản:
+ Dạng toán chuyển động
+ Dạng toán liên quan đến các kiến thức hình học
+ Dạng toán công việc làm chung, làm riêng
+ Dạng toán chảy chung, chảy riêng của vòi nước
+ Dạng toán tìm số
+ Dạng toán sử dụng các kiến thức về %
+ Dạng toán sử dụng các kiến thức vật lý, hóa học
Các công thức cần lưu ý khi giải bài toán bằng cách lập phương trình, hệ phương trình:
+ Thời gian t, quãng đường s, vận tốc v: s = v.t, v = s/t, t = s/v
+ Chuyển động của tàu thuyền khi có tác động dòng nước:
V xuôi dòng = V thực + V dòng nước
V ngược dòng = V thực – V dòng nước
+ Khối lượng công việc A, năng suất lao động N, thời gian làm việc T: A = N.T
II. Bài tập áp dụng:
Bài 1: Quãng đường AB dài 120km. Hai ô tô khởi hành cùng một lúc đi từ A đến B, ô tô thứ nhất chạy nhanh hơn ô tô thứ hai 10km/h nên đến B trước ô tô thứ hai 24 phút. Tính vận tốc mỗi xe.
Giải:
Gọi vận tốc ô tô thứ nhất là x (km/h), (x>0)
Ta có vận tốc ô tô thứ hai là (x-10) (km/h)
Thời gian ô tô thứ nhất đi hết quãng đường AB là (h)
Thời gian ô tô thứ hai đi hết quãng đường AB là (h)
Vì ô tô thứ nhất chạy nhanh hơn ô tô thứ hai 10km/h nên đến B trước ô tô thứ hai 24 phút (h)
Do đó ta có phương trình:
Giải phương trình ta được: 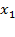 =60 (nhận),
=60 (nhận), 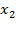 =-50 (loại)
=-50 (loại)
Vậy vận tốc của ô tô thứ nhất là 60km/h, vận tốc của ô tô thứ hai là 50km/h
Bài 2: Một ô tô du lịch đi từ A đến C. Cùng lúc từ địa điểm B nằm trên đoạn AC có một Ô tô vận tải cùng đi đến C. Sau 5 giờ hai Ô tô gặp nhau tại C. Hỏi Ô tô du lịch đi từ A đến B mất bao lâu , biết rằng vận tốc của Ô tô tải bằng vận tốc của Ô tô du lịch.
Lời Giải:
Gọi thời gian ô tô du lịch đi từ A đến B là x ( h ). ( 0 < x< 5 ).
Ta có thời gian ô tô du lịch đi từ B đến C là ( 5 – x) ( h ).
Bài 3: Trong lúc học nhóm, bạn Hùng yêu cầu bạn Minh và bạn Lan mỗi người chọn một số sao cho hai số này hơn kém nhau là 15 và tích của chúng phải bằng 150. Vậy hai bạn Minh và Lan phải chọn những số nào.
Giải
Gọi số nhỏ là x (x ), thì số lớn là x + 5
Vì tích của hai số là 150 ta có phương trình: x(x + 5) = 150 x2 + 5x –150 = 0
Giải phương trình ta được x1 = 10; x2 = – 15 (Thỏa mãn điều kiện)
Vậy nếu 1 bạn chọn số 10 thì bạn kia phải chọn số 15
Nếu 1 bạn chọn số – 15 thì bạn kia phải chọn số – 10
Bài 4: Một khu vườn hình chữ nhật có chu vi 280m. Người ta làm một lối đi xung quanh vườn (thuộc đất vườn) rộng 2m, diện tích còn lại để trồng trọt là 4256 m2. Tính kích thước các cạnh của khu vườn đó.
Bài giải
Gọi một cạnh của khu vườn là x (m), (x<140)
Cạnh còn lại của khu vườn là (140-x) (m)
Do lối đi xung quanh vườn rộng 2m nên kích thước các cạnh còn lại là (x-4), (140-x-4) (m)
Vì diện tích còn lại để trồng trọt là 4256 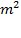 , do đó ta có phương trình:
, do đó ta có phương trình:
Giải phương trình ta được 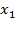 =80 (nhận),
=80 (nhận), 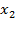 =60 (nhận)
=60 (nhận)
Vậy các cạnh của khu vườn hình chữ nhật là 80m, 60m.
Chúc các bạn học tốt.







