ÔN TẬP TOÁN HÌNH HỌC : ĐƯỜNG TRÒN

ÔN TẬP TOÁN HÌNH HỌC LỚP 9 HỌC KỲ 1: ĐƯỜNG TRÒN – CUNG – DÂY

Bài 1:

Cho tam giác ABC. Đường tròn có đường kính BC cắt AB, AC lần lượt tại E, D. BD và CE cắt nhau tại H, chứng minh:

a) AH vuông góc với BC ( tại F thuộc BC)

b) \[FA.FH=FB.FC\]

c) Bốn điểm A, E, H, D cùng nằm trên một đường tròn, xác định tâm I của đường tròn này.

d) IE là tiếp tuyến của đường tròn (O).

Giải

a) AH vuông góc với BC ( tại F thuộc BC)

Tam giác DBC nội tiếp (O) đường kính BC (gt)

\[\Rightarrow \]Tam giác DBC vuông tại D.

\[\Rightarrow \] BD 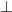CD hay BD 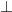AC.

Chứng mình CE 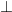AC.

Xét tam giác ABC, có

CE 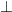AB (cmt) \[\Rightarrow \]CE là đường cao thứ nhất

BD \[\bot \] AC (cmt) \[\Rightarrow \] BD là đường cao thứ hai.

Hai đường cao BD và CE cắt nhau tại H (gt)

\[\Rightarrow \]H là trực tâm của tam giác ABC.

\[\Rightarrow \] AH là đường cao thứ ba.

\[\Rightarrow \]AH \[\bot \]BC tại F.

b) \[FA.FH=FB.FC\]

Xét \[\vartriangle FAB\] và \[\vartriangle FCH\], ta có:

\[\widehat{BFA}=\widehat{CFH}={{90}^{\circ }}\] (cmt)

\[\widehat{{{A}_{1}}}+\widehat{ABC}={{90}^{\circ }}(\vartriangle FAB\] vuông tại F)

\[\widehat{{{C}_{1}}}+\widehat{ABC}={{90}^{\circ }}(\vartriangle FAC\] vuông tại F)

\[\Rightarrow \widehat{{{A}_{1}}}=\widehat{{{C}_{1}}}(1)\]

\[\Rightarrow \vartriangle FAB\] đồng dạng \[\vartriangle FCH\].

\[\Rightarrow \frac{FA}{FC}=\frac{FB}{FH}\]

\[\Rightarrow FA.FH=FB.FC\].

c) A, E, H, D cùng nằm trên một đường tròn, xác định tâm I của đường tròn này.

Xét \[\vartriangle AEH\] vuông tại E (gt)

\[\Rightarrow \]\[\vartriangle AEH\] nội tiếp đường tròn đường kính AH

Hay A, E, H nằm trên đường tròn đường kính AH (1).

Xét \[\vartriangle ADH\] vuông tại D (gt)

\[\Rightarrow \]\[\vartriangle ADH\] nội tiếp đường tròn đường kính AH

Hay A, E, H nằm trên đường tròn đường kính AH (2)

Từ (1) và (2): A, E, H, D nằm trên đường tròn đường kính AH.

d) IE là tiếp tuyến của đường tròn (O).

Xét \[\vartriangle AEI\], ta có \[IA=IE\] ( bán kính)

\[\Rightarrow \]\[\vartriangle AEI\] cân tại I. (1)

\[\Rightarrow \widehat{{{A}_{1}}}=\widehat{{{E}_{1}}}\] (2)

Cmtt, ta được \[\widehat{{{C}_{1}}}=\widehat{{{E}_{3}}}\] (3)

Từ (1), (2) và (3), ta được: \[\widehat{{{E}_{1}}}\]= \[\widehat{{{E}_{3}}}\]

Mà \[\widehat{{{E}_{1}}}+\widehat{{{E}_{2}}}={{90}^{\circ }}\] \[\Rightarrow \widehat{{{E}_{3}}}+\widehat{{{E}_{2}}}={{90}^{\circ }}\]

Hay \[\widehat{IEO}={{90}^{\circ }}\]

\[\Rightarrow IE\bot EO\] tại E.

Mà E thuộc (O)

Vậy IE là tiếp tuyến của đường tròn (O).

Bài 2:

Trên tiếp tuyến tại điểm A của đường tròn (O; R) lấy điểm M. Gọi điểm B của đường tròn (O; R) sao cho MB = MA.

1. Chứng minh: MB là tiếp tuyến của đường tròn (O; R) .

2. Cho OM = 2R. Chứng minh : tam giác ABC đều.

Tính độ dài các cạnh và diện tích của tam giác AMB theo R

3. Vẽ đường kính BE của (O). Chứng minh AE // OM

Giải

1. MB là tiếp tuyến của đường tròn (O; R) .

Xét \[\vartriangle AOM\] và \[\vartriangle BOM\], ta có

\[MA=MB\] (gt)

\[OA=OB\] (bán kính)

OM là cạnh chung \[\Rightarrow \vartriangle AOM=\vartriangle BOM\]

\[\Rightarrow \widehat{MBO}=\widehat{MAO}\]

Mà \[\widehat{MAO}={{90}^{\circ }}\] (MA là tiếp tuyến của (O))

\[\Rightarrow \widehat{MBO}={{90}^{\circ }}\]

Hay \[MB\bot OB\] tại B

Mà điểm B của đường tròn (O; R)

Vậy MB là tiếp tuyến của đường tròn (O; R).

2. Cho OM = 2R

Xét \[\vartriangle AOM\] vuông tại A, ta có:

\[\sin OMA=OA:OM=\frac{1}{2}\]\[\Rightarrow \widehat{OMA}={{30}^{\circ }}\]

Mặt khác: \[\widehat{AMB}=2\widehat{OMA}={{60}^{\circ }}\] ( tính chất TT cắt nhau)

Xét \[\vartriangle ABM\]. Ta có MA = MB (gt)

\[\Rightarrow \vartriangle ABM\] cân tại M

Mà \[\widehat{AMB}\]\[={{60}^{\circ }}\] (cmt) \[\Rightarrow \vartriangle ABM\] đều.

Xét tam giác vuông tại A, theo định lý ta có:

\[O{{M}^{2}}=M{{A}^{2}}.O{{B}^{2}}\]

\[{{\left( 2R \right)}^{2}}=M{{A}^{2}}.{{R}^{2}}\] \[\Rightarrow MA=R\sqrt{3}\]

Diện tích \[{{S}_{AOM}}=M{{A}^{2}}.\frac{\sqrt{3}}{2}=\frac{3\sqrt{3}{{R}^{2}}}{2}\].

3. Chứng minh AE // OM

Ta có MA = MB (gt)

OA = OB (bán kính )

\[\Rightarrow \] MO là đường trung trực AB

\[\Rightarrow \] OM \[\bot \]AB (1)

Xét \[\vartriangle ABE\] nội tiếp (O), có BE là đường kính.

\[\Rightarrow \vartriangle ABE\] vuông tại A

\[\Rightarrow AE\bot AB\](2)

Từ (1) và (2) ta có AE // OM.

Bài 3:

Cho nửa đường tròn (O; R) có đường kính AB, tiếp tuyến tại điểm M trên nửa đường tròn lần lượt cắt hai tiếp tuyến tại A và B ở C và D.

1. Chứng minh: AC + DB = CD

2. Chứng minh: tam giác COD vuông và \[AC.BD={{R}^{2}}\]

3. OC cắt AM tại E và OD cắt BM tại F. Chứng minh:

a) Tứ giác OEMF là hình chữ nhật

b) \[OE.OC=OF.OD={{R}^{2}}\]

c) \[EF\bot BD\]

d) Chứng minh : AB là tiếp tuyến của đường tròn có đường kính CD

e) AD cắt BC tại N. Chứng minh: NM // AC.

Giải

1. Chứng minh AC + DB = CD

CA = CM ( tính chất hai tt cắt nhau)

DB = DM (tính chất hai tt cắt nhau)

CD = CM + MD

\[\Rightarrow \]AC + DB = CD

2. tam giác COD vuông và \[AC.BD={{R}^{2}}\]

Ta có:

OD là tia phân giác góc BOM ( tính chất hai tt cắt nhau)

OC là tia phân giác góc COM ( tính chất hai tt cắt nhau)

Mà \[\widehat{BOM}\]và \[\widehat{COM}\] kề bù.

\[\Rightarrow OC\bot OD\] tại O

Hay \[\vartriangle COD\] vuông tại O

Trong \[\vartriangle COD\] vuông tại O, đường cao OM, ta có hệ thức lượng:

\[MC.MD=O{{M}^{2}}={{R}^{2}}\]

Hay \[AC.BD={{R}^{2}}\] (CA = CM và DB = DM)

3. a) Tứ giác OEMF là hình chữ nhật

Ta có:

CA = CM (cmt)

OA = OM ( bán kính)

\[\Rightarrow \] CO là đường trung trực của AM

\[\Rightarrow \] \[CO\bot AM\] tại E; EA = EM

\[\Rightarrow \widehat{MEO}={{90}^{\circ }}\]

Cmtt, ta được \[\widehat{MFO}={{90}^{\circ }}\]

Tứ giác OEMF ta có: \[\widehat{MEO}=\widehat{MFO}=\widehat{FOE}={{90}^{\circ }}\]

\[\Rightarrow \] Tứ giác OEMF là hình chữ nhật

Trong \[\vartriangle COM\] vuông tại M, có đường cao ME, có hệ thức lượng

\[OC.OE=O{{M}^{2}}={{R}^{2}}\]

Cmtt: \[OD.OF=O{{M}^{2}}={{R}^{2}}\]

\[\Rightarrow OE.OC=OF.OD={{R}^{2}}\]

c)\[EF\bot BD\]

Xét \[\vartriangle ABM\], ta có:

EA = EM (cmt)

FB = FM (cmt)

\[\Rightarrow \] EF là đường trung bình

\[\Rightarrow \]EF // AB

Mà \[AB\bot BD\] ( tính chất tt)

\[\Rightarrow \]\[EF\bot BD\].

trong\[\vartriangle COD\] vuông tại O (cmt)

\[\Rightarrow \vartriangle COD\] nội tiếp đường tròn (I) đường kính CD

\[\Rightarrow IC=ID\]

Mặt khác CA // BD ( cùng vuông góc AB)

\[\Rightarrow \]tứ giác ABDC là hình thang

Xét thình thang ABDC, ta có:

IC = ID (cmt)

OA = OB ( AB là đường kính (O))

\[\Rightarrow \] IO là đường trung bình

\[\Rightarrow \] IO // CA

Mà \[CA\bot AB\]\[\Rightarrow \]\[IO\bot AB\] tại o

Mà điểm O thuộc (I) \[\Rightarrow \] AB là tiếp tuyến (I) đường kính CD.

ta có AC // BD (cmt)

\[\Rightarrow \frac{NA}{AC}=\frac{ND}{BD}\] (định lý Talet thuận)

Mà CA = CM và DB = DM (cmt)

\[\Rightarrow \frac{NA}{CM}=\frac{ND}{MD}\]

\[\Rightarrow \] NM // AC ( định lý Talet đảo)

BÀI TẬP RÈN LUYỆN

Bài 1

Cho tam giác ABC có 3 góc nhọn, kẻ hai đường cao BD và CE cắt nhau tại H.

1. Chứng minh bốn điểm A, E, H, D cùng thuộc một đường tròn. Xác định tâm I của đường tròn đó.

2. Chứng minh AH vuông góc BC.

3. Cho góc A = 60^o, AB = 6cm. Tính BD.

4. Gọi O là trung điểm của BC. Chứng minh OD là tiếp tuyến của đường tròn (I).

Bài 2

Cho đường tròn (O; R), đường kính AB. Lấy điểm C tùy ý trên cung AB sao cho AB < AC.

a) Chứng minh tam giác ABC vuông

b) Qua A vẽ tiếp tuyến (d) với đường tròn (O), BC cắt (d) tại F. Qua C vẽ tiếp tuyến (d’) với đường tròn (O), (d’) cắt (d) tại D. Chứng minh: DA = DF

c) Hạ CH vuông góc AB ( H thuộc AB), BD cắt CH tại K. Chứng minh K là trung điểm CH

d) Tia AK cắt CD tại E. Chứng mình EB là tiếp tuyến của (O), suy ra OE // CA.

Bài 3.

Cho đường tròn (O;R) và điểm A nằm ngoài đường tròn sao cho OA = 2R . Vẻ các tiếp tuyến AB ; AC với (O) ( B ; C là các tiếp điểm )

a) C/m: Tam giác ABC đều

b) Từ O kẻ đường vuông góc vớiOBcắt AC tại S . C/m : SO = SA

c) Gọi I là trung điểm của OA . C/minh SI là tiếp tuyến của (O)

d) Tính độ dài SI theo R.

Bài 4 :

Cho đường tròn (O;R) đường kính AB.H là trung điểm của OB.Qua H vẽ dây CD vuông

góc với AB.

a) Chứng minh tam giác OCB đều.

b) Tính đô dài AC và CH theo R.

c) Tiếp tuyến tại C và D cắt nhau ở I.Chứng tỏ 3 điểm O,B,I thẳng hàng và

4HB.HI = 3R²

d) Đường vuông góc với AD kẻ từ H cắt CB ở E; OE cắt CI tại K.Chứng minh KB

là tiếp tuyến của (O) và B là tâm đường tròn nội tiếp tam giác ICD.

Bài 5

Từ một điểm A ở ngoài (O; R), kẻ tiếp tuyến AB với (O) (B là tiếp điểm). Đường thẳng qua B và vuông góc với AO tại H cắt (O) tại C. Vẽ đường kính BD của (O).

a) Chứng minh ΔBCD vuông.

b) Chứng minh AC là tiếp tuyến của (O).

c) Chứng minh DC. AO = 2R² .

d) Biết OA = 2R. Tính diện tích ΔBCK theo R.

Bài 6

Từ một điểm M ở ngoài đường tròn (O) vẽ hai tiếp tuyến MA và MB (A và B là hai tiếp điểm), OM cắt AB tại H.

1) Chứng minh H là trung điểm của AB.

2) Trên đường thẳng AB lấy điểm N (với A nằm giữa B và N). Từ M kẻ một đường thẳng vuông góc với ON tại K và cắt AB tại I. Chứng minh 5 điểm O, K, A, M, B cùng nằm trên một đường tròn.

3) Chứng minh : NA.NB = NI.NH

4) Tia MK cắt đường tròn (O) tại C và D (với C nằm giữa M và D). Chứng minh NC và ND là hai tiếp tuyến của đường tròn (O).

Bài 7

Cho điểm M nằm ngoài đường tròn (O;R) vớiOM= 2R từ M kẻ hai tiếp tuyến MA,MB (A,B là hai tiếp điểm)

a) Chứng minhOM\[\bot \]AB. Tính MA theo R.

b) Đường thẳng vuông góc OA tại O cắt MB tại I.chứng minh ∆MOI cân.

c) Gọi H là giao điểm của OM với cung nhỏ AB, tia IH cắt MA tại J.

Chứng minh tứ giác OIMJ là hình thoi.

d) Tính diện tích AJIB theo R.