HÀM SỐ LIÊN TỤC
A/ LÝ THUYẾT
I/ Định nghĩa hàm số liên tục
+ Cho hàm số
$y=f(x)$ xác định trên khoảng K và ${{x}_{0}}\in K$
Hàm số $y=f(x)$
được gọi là liên tục tại ${{x}_{0}}$ nếu $\underset{x\to
{{x}_{0}}}{\mathop{\lim }}\,f(x)=f({{x}_{0}})$
+ Hàm số $y=f(x)$
được gọi là liên tục trên một khoảng nếu nó liên tục tại mọi điểm thuộc khoảng
đó.
+ Hàm số $y=f(x)$
được gọi là liên tục trên một đoạn $\left[ a;b \right]$ nếu nó liên tục trên
khoảng $(a;b)$ và $\underset{x\to {{a}^{+}}}{\mathop{\lim }}\,f(x)=f(a)$ ; $\underset{x\to
{{b}^{-}}}{\mathop{\lim }}\,f(x)=f(b)$
Chú
ý: Đồ thị hàm số liên tục trên một khoảng là một đường liền trên khoảng đó.
II/ Các định lí
1/ Định lí 1
a/ Hàm số đa
thức liên tục trên toàn bộ tập số thực R
b/ Hàm số
phân thức hữu tỉ và hàm số lượng giác liên tục trên từng khoảng xác định của nó
2/ Định lí 2
Giả sử $y=f(x)$
và $y=g(x)$ là hai hàm số liên tục tại ${{x}_{0}}$ . Khi đó:
a/ Các hàm số
$y=f(x)+g(x)$ , $y=f(x)-g(x)$ , $y=f(x).g(x)$ cũng liên tục tại ${{x}_{0}}$
b/ Hàm số $y=\frac{f(x)}{g(x)}$
liên tục tại ${{x}_{0}}$nếu $g({{x}_{0}})\ne 0$
3/ Định lí 3
Nếu hàm số $y=f(x)$
liên tục trên đoạn $\left[ a;b \right]$ và $f(a)f(x)<0$ thì tồn tại ít nhất
một điểm sao cho $f(c)=0$
Hay:
Nếu hàm số $y=f(x)$
liên tục trên đoạn $\left[ a;b \right]$ và $f(a)f(x)<0$ thì phương trình $f(x)=0$
tồn tại ít nhất một nghiêm ${{x}_{0}}\in \left( a;b \right)$
4/ Định lý 4 (định lý giá trị trung gian)
Nếu hàm số $y=f(x)$
liên tục trên đoạn $\left[ a;b \right]$ và $f(a)\ne f(b)$ thì với mọi số thực M
nằm giữa f(a) và f(b) luôn tồn tại ít nhất một điểm $c\in \left( a;b \right)$
sao cho $f(c)=M$
B/ VÍ DỤ
VD 1: Cho hàm số 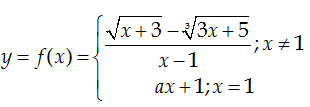
Tìm a để hàm số $y=f(x)$ liên tục tại x = 1
A.-1
B.$-\frac{13}{12}$
C.$\frac{11}{12}$
D.$\frac{1}{6}$
Giải:
Ta có: $\underset{x\to
1}{\mathop{\lim }}\,f(x)=\underset{x\to 1}{\mathop{\lim
}}\,\frac{\sqrt{x+3}-\sqrt[3]{3x+5}}{x-1}=\underset{x\to 1}{\mathop{\lim
}}\,\frac{\sqrt{x+3}-2}{x-1}-\underset{x\to 1}{\mathop{\lim
}}\,\frac{\sqrt[3]{3x+5}-2}{x-1}$
$=\underset{x\to
1}{\mathop{\lim }}\,\frac{x-1}{(x-1)(\sqrt{x+3}+2)}-\underset{x\to
1}{\mathop{\lim }}\,\frac{3(x-1)}{(x-1)\left[
\sqrt[3]{{{(3x+5)}^{2}}}+2\sqrt[3]{3x+5}+4 \right]}$
$=\underset{x\to
1}{\mathop{\lim }}\,\frac{1}{\sqrt{x+3}+2}-\underset{x\to 1}{\mathop{\lim
}}\,\frac{3}{\left[ \sqrt[3]{{{(3x+5)}^{2}}}+2\sqrt[3]{3x+5}+4 \right]}$
$=\frac{1}{4}-\frac{3}{12}=0$
Để hàm số
liên tục tại x = 1 thì $f(1)=a+1=0\Leftrightarrow a=-1$
Đáp án A
VD 2: Cho hàm số 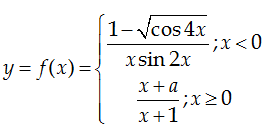
Để hàm số
liên tục tại x = 0 thì giá trị của a là bao nhiêu?
A.2
B.0
C.1
D.$\frac{1}{2}$
Giải:
Ta có: $\underset{x\to
{{0}^{+}}}{\mathop{\lim }}\,f(x)=f(0)=a$
$\underset{x\to
{{0}^{-}}}{\mathop{\lim }}\,f(x)=\underset{x\to {{0}^{-}}}{\mathop{\lim
}}\,\frac{1-\sqrt{\cos 4x}}{x\sin 2x}=\underset{x\to {{0}^{-}}}{\mathop{\lim
}}\,\frac{2{{\sin }^{2}}2x}{x\sin 2x(1+\sqrt{\cos 4x})}$
$=\underset{x\to
{{0}^{-}}}{\mathop{\lim }}\,\frac{2.2\sin 2x}{2x}.\frac{1}{1+\sqrt{\cos
4x}}=\frac{4}{1+1}=2$
Đáp án A
VD 3: Cho hàm số 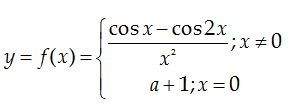
Tìm a để hàm
số liên tục tại x = 0?
A.$\frac{1}{2}$
B.$\frac{1}{3}$
C.$\frac{1}{4}$
D.$\frac{1}{5}$
Giải:
Ta có:
$\underset{x\to
0}{\mathop{\lim }}\,f(x)=\underset{x\to 0}{\mathop{\lim }}\,\frac{\cos x-\cos
2x}{{{x}^{2}}}$
$=\underset{x\to
0}{\mathop{\lim }}\,\frac{2\sin \frac{3x}{2}}{x}.\underset{x\to 0}{\mathop{\lim
}}\,\frac{\sin \frac{x}{2}}{x}=\frac{3}{2}.\underset{x\to 0}{\mathop{\lim
}}\,\frac{\sin \frac{3x}{2}}{\frac{3x}{2}}.\underset{x\to 0}{\mathop{\lim
}}\,\frac{\sin \frac{x}{2}}{\frac{x}{2}}=\frac{3}{2}.1.1=\frac{3}{2}$
Mà $f(0)=a+1$
Để hàm số
liên tục tại x = 0 thì:
$\underset{x\to
0}{\mathop{\lim }}\,f(x)=f(0)\Leftrightarrow a+1=\frac{3}{2}\Leftrightarrow
a=\frac{1}{2}$
Đáp án A
VD 4: Trong các khoảng sau đây, khoảng nào
chứa ít nhất một nghiệm của phương trình: ${{x}^{5}}+{{x}^{4}}-2{{x}^{3}}+4{{x}^{2}}-1=0$
A.$(1;2)$
B.$\left(
0;\frac{1}{2} \right)$
C.$(-2;-1)$
D.$\left(
-1;0 \right)$
Giải:
Ta có hàm số
$y=f(x)={{x}^{5}}+{{x}^{4}}-2{{x}^{3}}+4{{x}^{2}}-1$ liên tục trên R (vì hàm đa
thức)
Xét:
$f(1)=3;f(2)=47;f(1).f(2)>0$
$f(0)=-1;f\left(
\frac{1}{2} \right)=-\frac{5}{32};f(-1).f\left( \frac{1}{2} \right)>0$
$f(-2)=15;f(-1)=5;f(-2).f(-1)>0$
$f(-1)=5;f(0)=-1;f(-1).f(0)<0$
Ta thấy $f(-1).f(0)<0$
nên trong khoảng $(-1;0)$ chứa ít nhất một nghiệm của phương trình đã cho.
Đáp án D
VD 5: Phương trình $9{{x}^{4}}-36{{x}^{3}}+37{{x}^{2}}-9=0$
có bao nhiêu nghiệm thực phân biệt?
A.Vô nghiệm
B.1
C.3
D.4
Giải:
Ta thấy hàm
số $y=f(x)=9{{x}^{4}}-36{{x}^{3}}+37{{x}^{2}}-9$ liên tục trên R (vì hàm đa thức)
Ta có:
$f(-1)=73;f(0)=-9;f(-1).f(0)<0\Rightarrow
$ có 1 nghiệm x thuộc đoạn$(-1;0)$
$f(0)=-9;f(1)=1;f(0).f(1)<0\Rightarrow
$ có 1 nghiệm x thuộc đoạn $(0;1)$
$f(1)=1;f(2)=-5;f(1).f(2)<0\Rightarrow
$ có 1 nghiệm x thuộc đoạn $(1;2)$
$f(2)=-5;f(3)=81;f(2).f(3)<0\Rightarrow
$ có 1 nghiệm x thuộc đoạn $(2;3)$
Vậy phương
trình đã cho có 4 nghiệm phân biệt
Đáp án D
C/ BÀI TẬP
Bài 1: Tìm phát biểu sai: 1
A.Hàm số $y=f(x)=\frac{\sqrt{1+x}-1}{\sqrt[3]{1+x}-1}$
liên tục tại x = 0 nếu $f(0)=\frac{3}{2}$
B.Hàm số $y=f(x)=\frac{\tan
2x}{x}$ liên tục tại x = 0 nếu $f(0)=2$
C.Hàm số $y=f(x)=x.\sin
\frac{1}{x}$ liên tục tại x = 0 nếu $f(0)=1$
D.Hàm số $y=f(x)={{2}^{\frac{1}{{{x}^{2}}}}}$
liên tục tại x = 0 nếu $f(0)=0$
Bài 2: Cho hàm số 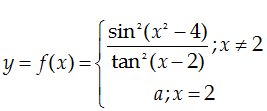
Tìm a để hàm
số đã cho liên tục tại x = 2?
A.4
B.8
C.12
D.16
Bài 3: Cho phương trình: $\cos x+m\cos 2x=0$
. Kết luận nào sau đây là đúng?
A.Với mọi m,
phương trình có ít nhất một nghiệm thuộc đoạn $\left( \frac{\pi }{4};\frac{\pi
}{2} \right)$
B.Với mọi m,
phương trình có ít nhất một nghiệm thuộc đoạn $\left( \frac{\pi }{4};\frac{3\pi
}{4} \right)$
C.Với mọi m,
phương trình có ít nhất một nghiệm thuộc đoạn $\left( -\frac{\pi }{4};\frac{\pi
}{4} \right)$
D.Với mọi m,
phương trình có ít nhất một nghiệm thuộc đoạn $\left( -\frac{\pi }{4};0
\right)$
Bài 4: Cho phương trình: $m{{(x-1)}^{3}}(x+2)+2x+3=0$
. Kết luận nào sau đây là đúng? 7
A.Với mọi m,
phương trình có ít nhất một nghiệm thuộc đoạn $(-1;1)$
B.Với mọi m,
phương trình có ít nhất một nghiệm thuộc đoạn $(-1;0)$
C.Với mọi m,
phương trình có ít nhất một nghiệm thuộc đoạn $(0;1)$
D.Với mọi m,
phương trình có ít nhất một nghiệm thuộc đoạn $(-2;1)$
Bài 5: Cho phương trình: $({{m}^{2}}-m+1){{x}^{4}}+2x-2=0$
. Kết luận nào sau đây là đúng?
A.Với mọi m,
phương trình có ít nhất một nghiệm thuộc đoạn $(-1;0)$
B.Với mọi m,
phương trình có ít nhất một nghiệm thuộc đoạn $(0;1)$
C.Với mọi m,
phương trình có ít nhất một nghiệm thuộc đoạn $(-2;-1)$
D.Với mọi m,
phương trình có ít nhất một nghiệm thuộc đoạn $(1;2)$
Bài 6: Trong các khoảng dưới đây, khoảng nào chứa ít nhất một nghiệm
của phương trình: ${{x}^{5}}+{{x}^{4}}-2{{x}^{3}}+4{{x}^{2}}-1=0$ ?
A.$(-2;-1)$
B.$(1;2)$
C.$(-1;0)$
D.$\left(
0;\frac{1}{2} \right)$
Bài 7: Phương trình $9{{x}^{4}}-36{{x}^{3}}+37{{x}^{2}}-9=0$
có bao nhiêu nghiệm phân biệt?
A.3
B.4
C.Vô nghiệm
D.2
Bài 8: Chọn phát biểu sai:
A.Hàm số $y=f(x)=\frac{3x+2}{x-1}$
gián đoạn tại x = 1
B.Hàm số $y=g(x)=\frac{{{x}^{2}}+3}{{{x}^{2}}+4}$
gián đoạn tại x = 2
C.Hàm số $y=p(x)=\frac{\left|
x \right|}{x}$ gián đoạn tại x = 0
D.Hàm số $y=q(x)=\frac{\cot
x}{x}$ không liên tục trên R
Bài 9: Cho hàm số: 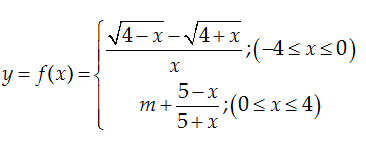
Tìm giá trị
của m để hàm số liên tục trên đoạn $\left[ -4;4 \right]$ ?
A.$-\frac{1}{2}$
B.-1
C.$-\frac{3}{2}$
D.-2
Bài 10: Cho hàm số: 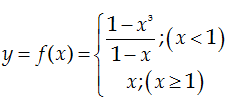
Kết luận nào
sau đây là đúng?
A.Hàm số đã
cho không liên tục tại x = 1
B.Hàm số đã
cho liên tục bên phải tại x = 1
C.Hàm số đã
cho liên tục bên trái tại x = 1
D.Hàm số đã
cho liên tục trên R
ĐÁP ÁN
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
C |
D |
B |
D |
B |
C |
B |
B |
C |
A |







