PHƯƠNG PHÁP GIẢN ĐỒ VECTOR (Phần 1)
1. Phương pháp vector trượt
&
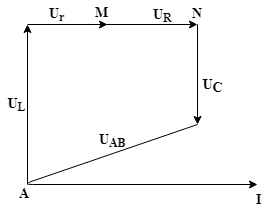
Chọn trục ngang là trục dòng điện.
&Chọn
điểm A đầu mạch làm gốc.
&Vẽ
lần lượt từ A sang B theo nguyên tắc nối đuôi nhau:
L
– đi lên
R
– đi ngang
C
– đi xuống
Ví dụ:

Ví
dụ 1: Đoạn mạch xoay chiều gồm điện trở thuần 30 $\Omega
$ mắc nối tiếp với cuộn dây. Điện áp hiệu dụng ở hai đầu cuộn dây là 120 V.
Dòng điện trong mạch lệch pha $\text{ }\!\!\pi\!\!\text{ /6}$ so với điện áp
hai đầu đoạn mạch và lệch pha $\text{ }\!\!\pi\!\!\text{ /3}$ so với điện áp
hai đầu cuộn dây. Tính cường độ hiệu dụng dòng qua mạch.
Hướng dẫn:
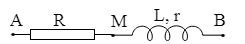
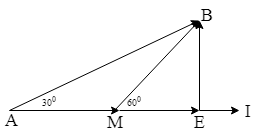
$\Delta $AMB cân tại M $\Rightarrow $ ${{\text{U}}_{\text{R}}}$
= MB = 120 (V) $\Rightarrow $ I = $\frac{{{\text{U}}_{\text{R}}}}{\text{R}}$ =
4 (A)
Ví
dụ 2: Đoạn mạch xoay chiều gồm điện trở thuần R mắc nối
tiếp với cuộn dây. Điện áp hiệu dụng ở hai đầu điện trở, cuộn dây và hai đầu đoạn
mạch lần lượt là 35 V, 85 V và $75\sqrt{2}$ V. Cuộn dây tiêu thụ công suất 40
W. Tính tổng điện trở thuần của toàn mạch.
Hướng dẫn
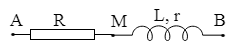
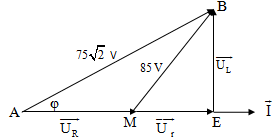
cos$\text{ }\!\!\varphi\!\!\text{ }$ = $\frac{{{35}^{2}}+{{\left(
75\sqrt{2} \right)}^{2}}-{{85}^{2}}}{2.35.75\sqrt{2}}$ = $\frac{\sqrt{2}}{2}$
$\Rightarrow $ ${{\text{U}}_{\text{R+r}}}$ = AE =
ABcos$\text{ }\!\!\varphi\!\!\text{ }$ = 75 (V) $\Rightarrow $ ${{\text{U}}_{\text{r}}}$
= 45 (V)
${{\text{P}}_{\text{r}}}$ = ${{\text{I}}^{\text{2}}}\text{R}$
= $\text{I}{{\text{U}}_{\text{r}}}$ $\Rightarrow $ I = $\frac{{{\text{P}}_{\text{r}}}}{{{\text{U}}_{\text{r}}}}$
= 1 (A)
$\Rightarrow $ r + R = $\frac{{{\text{U}}_{\text{R+r}}}}{\text{I}}$ = 75 ($\Omega $)
Ví
dụ 3: Đặt một điệp áp xoay chiều có giá trị hiệu dụng
200 V vào hai đầu đoạn mạch AB gồm cuộn cảm thuần có độ tự cảm L, điện trở thuần
R và tụ điện có điện dung C mắc nối tiếp theo thứ tự trên. Điện áp hiệu dụng
trên L là $200\sqrt{2}$ V và trên đoạn chứa RC là 200 V. Tính điện áp hiệu dụng
giữa hai đầu tụ điện?
Hướng dẫn

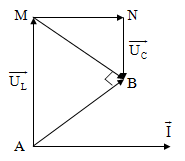
$\Delta $AMB vuông cân tại B $\Rightarrow $ $\widehat{\text{AMB}}$
= ${{45}^{0}}$ $\Rightarrow $ $\widehat{\text{NMB}}$ = ${{45}^{0}}$
$\Rightarrow $ $\Delta $NMB vuông cân tại N $\Rightarrow
$ ${{\text{U}}_{\text{C}}}$ = $\frac{\text{NB}}{\sqrt{\text{2}}}$ = $100\sqrt{2}$
(V)
Ví
dụ 4: Mạch điện gồm cuộn dây mắc nối tiếp với tụ điện
C. Đặt vào hai đầu đoạn mạch điệp áp xoay chiều 200 V – 50 Hz thì điện áp hai đầu
cuộn dây và hai đầu tụ điện có cùng giá trị hiệu dụng nhưng lệch pha nhau ${{120}^{0}}$.
Điện áp hiệu dụng trên tụ là bao nhiêu?
Hướng dẫn

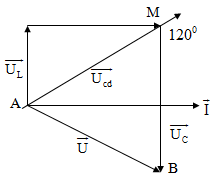
$\Delta $AMB là tam giác đều $\Rightarrow $ ${{\text{U}}_{\text{C}}}$
= U = 200 (V)
Ví
dụ 5: Đặt điện áp u = ${{\text{U}}_{\text{0}}}$cos$\text{
}\!\!\omega\!\!\text{ }$t (${{\text{U}}_{\text{0}}}$ và $\text{
}\!\!\omega\!\!\text{ }$ không đổi) vào hai đầu đoạn mạch AB theo thứ tự gồm một
tụ điện, một cuộn cảm thuần và một điện trở thuần mắc nối tiếp. Gọi M là điểm nối
giữa tụ điện và cuộn cảm. Biết điện áp hiệu dụng giữa hai đầu AM bằng điện áp
hiệu dụng giữa hai đầu MB và cường độ dòng điện trong đoạn mạch lệch pha ${{20}^{0}}$
so với điện áp giữa hai đầu đoạn mạch. Tính hệ số công suất của đoạn mạch MB.
Hướng dẫn

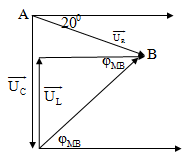
$\Delta $AMB cân tại M nên ${{20}^{0}}$ + ${{\text{
}\!\!\varphi\!\!\text{ }}_{\text{MB}}}$ = ${{70}^{0}}$ $\Rightarrow $ cos${{\text{
}\!\!\varphi\!\!\text{ }}_{\text{MB}}}$ = 0,64
Ví
dụ 6: Đặt điệp áp xoay chiều tần số 50 Hz vào hai đầu
đoạn mạch AB gồm hai đoạn mạch AM và MB mắc nối tiếp. Đoạn AM gồm điện trở thuần
$100\sqrt{3}$ $\Omega $ mắc nối tiếp với cuộn cảm thuần có độ tự cảm L, đoạn MB
chỉ có tụ điện có điện dung $\text{0,05/ }\!\!\pi\!\!\text{ }$ mF. Biết điện áp
giữa hai đầu đoạn mạch MB và điện áp giữa hai đầu đoạn mạch AB lệch pha nhau $\text{
}\!\!\pi\!\!\text{ /3}$. Tính L.
Hướng dẫn
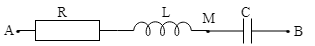

${{\text{Z}}_{\text{C}}}$ = $\frac{\text{1}}{\text{
}\!\!\omega\!\!\text{ C}}$ = 200 ($\Omega $)
BE = AEcot$\frac{\text{ }\!\!\pi\!\!\text{
}}{\text{3}}$ = 100 ($\Omega $)
${{\text{Z}}_{\text{L}}}$ = ${{\text{Z}}_{\text{C}}}$
- BE = 100($\Omega $) $\Rightarrow $ L = $\frac{{{\text{Z}}_{\text{L}}}}{\text{
}\!\!\omega\!\!\text{ }}$ = $\frac{\text{1}}{\text{ }\!\!\pi\!\!\text{ }}$ (H)
Ví
dụ 7: Một đoạn mạch điện xoay chiều gồm một tụ điện có
dung kháng 200 $\Omega $ và một cuộn dây mắc nối tiếp. Khi đặt vào hai đầu đoạn
mạch trên một điệp áp xoay chiều luôn có biểu thức u = $120\sqrt{2}$cos(100$\text{
}\!\!\pi\!\!\text{ }$t + $\text{ }\!\!\pi\!\!\text{ }$/3) (V) thì thấy điện áp
giữa hai đầu cuộn dây có giá trị hiệu dụng là 120 V và sớm pha $\text{
}\!\!\pi\!\!\text{ }$/2 so với điện áp đặt vào mạch. Tính công suất tiêu thụ của
cuộn dây.
Hướng dẫn


$\Delta $AMB
vuông cân tại B: ${{\text{U}}_{\text{C}}}$ = $\sqrt{\text{M}{{\text{B}}^{\text{2}}}\text{+A}{{\text{B}}^{\text{2}}}}$
= $120\sqrt{2}$ (V)
Suy ra ${{\text{
}\!\!\varphi\!\!\text{ }}_{\text{cd}}}$ = ${{45}^{0}}$ ; I = $\frac{{{\text{U}}_{\text{C}}}}{{{\text{Z}}_{\text{C}}}}$
= $0,6\sqrt{2}$ (A)
$\Delta $MNB
vuông cân tại N: ${{\text{U}}_{\text{r}}}$ = $\frac{\text{MB}}{\sqrt{\text{2}}}$
= $60\sqrt{2}$ (V)
$\Rightarrow $ ${{\text{P}}_{\text{r}}}$
= ${{\text{I}}^{\text{2}}}$r = I${{\text{U}}_{\text{r}}}$ = 72 (W)
Ví dụ 8: Trên đoạn mạch xoay chiều ko phân nhánh có bốn điểm theo
thứ tự A, M, N và B. Giữa hai điểm A và M chỉ có cuộn dây, giữa hai điểm M và N
chỉ có điện trở thuần R = 60 $\Omega $, giữa hai điểm N và B chỉ có tụ điện. Điện
áp hiệu dụng hai điểm A và N là 120 V và điện áp hiệu dụng hai điểm M và B là $80\sqrt{3}$
V. Điện áp tức thời trên đoạn AN và trên đoạn MB lệch pha nhau ${{90}^{0}}$, điện
áp tức thời trên MB và trên NB lệch pha nhau ${{30}^{0}}$. Tính điện trở thuần
của cuộn dây.
Hướng dẫn

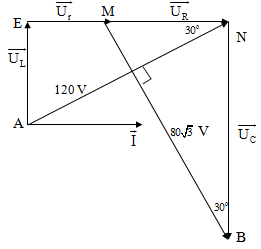
$\Delta $MNB: MN
= ${{\text{U}}_{\text{R}}}$ = MB.sin${{30}^{0}}$ = $40\sqrt{3}$ (V)
$\Delta $AEN: EN
= AN.cos${{30}^{0}}$ = $60\sqrt{3}$ (V)
$\Rightarrow $ ${{\text{U}}_{\text{r}}}$
= EN – MN = $20\sqrt{3}$ (V)
$\Rightarrow $ $\frac{\text{r}}{\text{R}}$
= $\frac{{{\text{U}}_{\text{r}}}}{{{\text{U}}_{\text{R}}}}$ = $\frac{1}{2}$ $\Rightarrow
$ r = $\frac{\text{R}}{\text{2}}$ = 30 ($\Omega $)
Ví dụ 9: Một mạch điện xoay chiều nối tiếp gồm tụ điện có điện
dung C, điện trở thuần R và cuộn dây có độ tực cảm L có điện trở thuần r. Dùng
vôn kế có điện trở rất lớn lần lượt đo hai đầu điện trở, hai đầu cuộn dây và
hai đầu đoạn mạch thì số chỉ lần lượt là 50 V, $30\sqrt{2}$ V và 80 V. Biết điện
áp tức thời trên cuộn dây sớm pha hơn dòng điện là $\text{ }\!\!\pi\!\!\text{
}$/4. Tính điện áp hiệu dụng trên tụ.
Hướng dẫn


$\Delta $ENB
vuông cân tại E: NE = EB = 30 (V)
$\Rightarrow $ ME = MN + NE = 80 (V) = AB
Tứ giác AMEB là
hình chự nhật $\Rightarrow $ ${{\text{U}}_{\text{C}}}$ = AM = EB = 30 (V)
Ví dụ 10: Đặt điệp áp xoay chiều có giá trị hiệu dụng 100 V vào hai đầu đoạn mạch AB như hình bên thì dòng điện qua mạch có cường độ là i = $2\sqrt{2}$ cos$\text{ }\!\!\omega\!\!\text{ }$t (A). Biết điện áp hiệu dụng ở hai đầu AM, MN và NB lần lượt là 30 V, 30 V và 100 V. Tính công suất tiêu thụ của đoạn mạch AB.
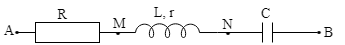
Hướng dẫn
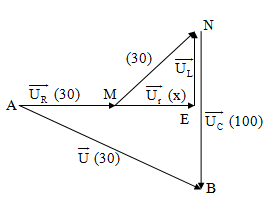
NE + EB = NB $\Rightarrow $ $\sqrt{\text{3}{{\text{0}}^{\text{2}}}\text{-}{{\text{x}}^{\text{2}}}}$
+ $\sqrt{\text{10}{{\text{0}}^{\text{2}}}\text{-}{{\left( \text{x+30}
\right)}^{\text{2}}}}$ = 100 $\Rightarrow $ x = 25
$\Rightarrow $ P = \[{{\text{I}}^{\text{2}}}\](R + r) = I(${{\text{U}}_{\text{R}}}$ + ${{\text{U}}_{\text{r}}}$) = 2(30 +25) = 110 (W)
2. Phương pháp vector trượt
&Chọn
trục ngang là trục dòng điện.
&Chọn
điểm O làm gốc.
&Vẽ
lần lược các vector biểu diễn các điện áp cùng chung gốc O theo nguyên tắc:
L
– đi lên
R
– đi ngang
C
– đi xuống
&Chỉ
tổng hợp các vector điện áp có liên quan đến dữ kiện của bài toán.
&Biểu
diễn các số liệu lên giản đồ
&Dựa
vào hệ thức lượng trong tam giác để tìm các dữ kiện liên quan
F Nhắc lại:
- Trong tam
giác vuông:
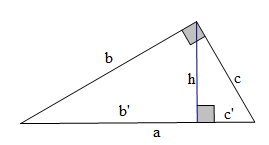
${{\text{a}}^{\text{2}}}$ = ${{\text{b}}^{\text{2}}}$
+ ${{\text{c}}^{\text{2}}}$
\[{{\text{h}}^{\text{2}}}\] = b’c’
$\frac{\text{1}}{{{\text{h}}^{\text{2}}}}$ = $\frac{\text{1}}{{{\text{b}}^{\text{2}}}}$
+ $\frac{\text{1}}{{{\text{c}}^{\text{2}}}}$
${{\text{b}}^{\text{2}}}$ = ab’; ${{\text{c}}^{\text{2}}}$
= ac’
- Trong tam giác thường:
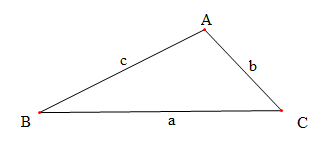
${{\text{a}}^{\text{2}}}$ = ${{\text{b}}^{\text{2}}}$
+ ${{\text{c}}^{\text{2}}}$ - 2bccosA
$\frac{\text{a}}{\text{sinA}}$ = $\frac{\text{b}}{\text{sinB}}$
= $\frac{\text{c}}{\text{sinC}}$
F Phương pháp vector buộc chỉ hiệu quả với các bài toán có R nằm giữa đồng thời liên quan đến điện áp bắt chéo $\overrightarrow{{{\text{U}}_{\text{AN}}}}$, $\overrightarrow{{{\text{U}}_{\text{MB}}}}$.

Ví
dụ 1: Trên đoạn mạch xoay chiều không phân nhánh có bốn
điểm theo đúng thứ tự A, M, N và B. Giữa 2 điểm A và M chỉ có cuộn cảm thuần,
giữa 2 điểm M và N chỉ có điện trở thuần, giữa 2 điểm N và B chỉ có tụ điện. Điện
áp hiệu dụng 2 điểm A và M là 150 V và điện áp hiệu dụng 2 điểm N và B là 200/3
V. Điện áp tức thời trên đoạn AN và trên đoạn MB lệch pha nhau ${{90}^{0}}$.
Tính điện áp hiệu dụng trên R.
Hướng dẫn

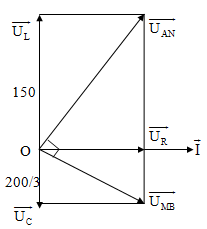
Vì liên quan đến $\overrightarrow{{{\text{U}}_{\text{AN}}}}$
$\bot $ $\overrightarrow{{{\text{U}}_{\text{MB}}}}$ nên ta tổng hợp theo quy tắc
hình bình hành với $\overrightarrow{{{\text{U}}_{\text{AN}}}}$ = $\overrightarrow{{{\text{U}}_{\text{R}}}}$
+ $\overrightarrow{{{\text{U}}_{\text{L}}}}$ ; $\overrightarrow{{{\text{U}}_{\text{MB}}}}$=
$\overrightarrow{{{\text{U}}_{\text{R}}}}$ + $\overrightarrow{{{\text{U}}_{\text{C}}}}$
Hệ thức lượng: \[{{\text{U}}_{\text{R}}}\] = $\sqrt{\frac{200}{3}.150}$ = 100 (V)
Ví
dụ 2: Trên đoạn mạch xoay chiều không phân nhánh có bốn
điểm theo đúng thứ tự A, M, N và B. Giữa 2 điểm A và M chỉ có cuộn cảm thuần,
giữa 2 điểm M và N chỉ có điện trở thuần, giữa 2 điểm N và B chỉ có tụ điện. Điện
áp hiệu dụng 2 điểm A và N là 400 V và điện áp hiệu dụng 2 điểm M và B là 300
V. Điện áp tức thời trên đoạn AN và trên đoạn MB lệch pha nhau ${{90}^{0}}$.
Tính điện áp hiệu dụng trên R.
Hướng dẫn

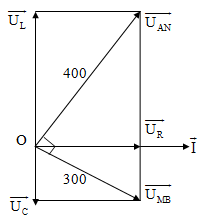
Vì liên quan đến $\overrightarrow{{{\text{U}}_{\text{AN}}}}$ $\bot $ $\overrightarrow{{{\text{U}}_{\text{MB}}}}$ nên ta tổng hợp theo quy tắc hình bình hành với $\overrightarrow{{{\text{U}}_{\text{AN}}}}$ = $\overrightarrow{{{\text{U}}_{\text{R}}}}$ + $\overrightarrow{{{\text{U}}_{\text{L}}}}$ ; $\overrightarrow{{{\text{U}}_{\text{MB}}}}$= $\overrightarrow{{{\text{U}}_{\text{R}}}}$ + $\overrightarrow{{{\text{U}}_{\text{C}}}}$
Hệ thức lượng: $\frac{\text{1}}{\text{U}_{\text{R}}^{\text{2}}}$ = $\frac{1}{{{300}^{2}}}$ + $\frac{1}{{{400}^{2}}}$ $\Rightarrow $ ${{\text{U}}_{\text{R}}}$ = 240 (V)
Ví
dụ 3: Mạch điện xoay chiều nối tiếp AB theo đúng thứ tự
gồm cuộn cảm thuần L, điện trở thuần R và tụ điện C. Cho biết điện áp hiệu dụng
${{\text{U}}_{\text{RC}}}$ = 0,75${{\text{U}}_{\text{RL}}}$ và ${{\text{R}}^{\text{2}}}$
= L/C. Tính hệ số công suất đoạn mạch AB.
Hướng dẫn



$\Rightarrow $ tan$\text{ }\!\!\alpha\!\!\text{ }$
= 0,75 $\Rightarrow $ cos$\text{ }\!\!\alpha\!\!\text{ }$ = 0,8; sin$\text{
}\!\!\alpha\!\!\text{ }$ = 0,6
${{\text{U}}_{\text{R}}}$ = 0,75acos$\text{
}\!\!\alpha\!\!\text{ }$ = 0,6a
${{\text{U}}_{\text{C}}}$ = 0,75asin$\text{
}\!\!\alpha\!\!\text{ }$ = 0,45a
${{\text{U}}_{\text{L}}}$ = acos$\text{
}\!\!\alpha\!\!\text{ }$ = 0,8a
$\Rightarrow $ cos$\text{ }\!\!\varphi\!\!\text{
}$ = \[\frac{\text{R}}{\text{Z}}\] = $\frac{{{\text{U}}_{\text{R}}}}{\sqrt{\text{U}_{\text{R}}^{\text{2}}\text{+}{{\left(
{{\text{U}}_{\text{L}}}\text{-}{{\text{U}}_{\text{C}}} \right)}^{\text{2}}}}}$
= 0,864
Ví
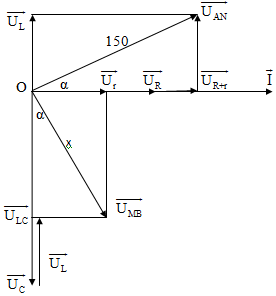
dụ 4: Trên đoạn mạch xoay chiều không phân nhánh có bốn
điểm theo đúng thứ tự A, M, N và B. Giữa 2 điểm A và M chỉ có điện trở thuần R,
giữa 2 điểm M và N chỉ có cuộn dây (có điện trở r = R/4). Giữa 2 điểm N và B chỉ
có tụ điện. Đặt vào hai đầu đoạn mạch một điện áp $100\sqrt{2}$ - 50 Hz thì điện
áp hiệu dụng trên đoạn AN bằng 150 V. Điện áp tức thời rên đoạn AN vuông pha với
điện áp trên đoạn MB. Tính điện áp hiệu dụng trên MB.
Hướng dẫn
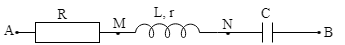
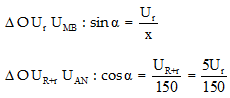
tan$\text{ }\!\!\alpha\!\!\text{ }$ = $\frac{\text{sin
}\!\!\alpha\!\!\text{ }}{\text{cos }\!\!\alpha\!\!\text{ }}$ = $\frac{\text{30}}{\text{x}}$
$\Rightarrow $ $\text{ }\!\!\alpha\!\!\text{ }$ = arctan$\frac{\text{30}}{\text{x}}$
(1)
${{\text{U}}^{\text{2}}}$ = $\text{U}_{\text{R+r}}^{\text{2}}$
+ $\text{U}_{\text{LC}}^{\text{2}}$ $\Leftrightarrow $ 2.${{100}^{2}}$ = ${{\left(
\text{150cos }\!\!\alpha\!\!\text{ } \right)}^{2}}$ + ${{\left( \text{xcos
}\!\!\alpha\!\!\text{ } \right)}^{2}}$ (2)
Từ (1), (2) $\Rightarrow $ x = 56,33 (V)







