QUAN HỆ GIỮA CÁC ĐẠI LƯỢNG TỨC THỜI
* Lí thuyết cần nhớ:
-
Mạch chỉ R thì u và i cùng pha nên R = $\frac{\text{U}}{\text{I}}$ = $\frac{{{\text{U}}_{0}}}{{{\text{I}}_{0}}}$
= $\frac{\text{u}}{\text{i}}$
-
Mạch chỉ L thì u sớm pha $\frac{\text{ }\!\!\pi\!\!\text{ }}{\text{2}}$ so với
i nên ${{\left( \frac{\text{i}}{{{\text{I}}_{\text{0}}}}
\right)}^{\text{2}}}\text{+}{{\left( \frac{\text{u}}{{{\text{U}}_{\text{0}}}}
\right)}^{\text{2}}}\text{=1}$
-
Mạch chỉ C thì u trễ pha $\frac{\text{ }\!\!\pi\!\!\text{ }}{\text{2}}$ so với
i nên ${{\left( \frac{\text{i}}{{{\text{I}}_{\text{0}}}}
\right)}^{\text{2}}}\text{+}{{\left( \frac{\text{u}}{{{\text{U}}_{\text{0}}}}
\right)}^{\text{2}}}\text{=1}$
-
Mạch gồm L, C thì ${{\left( \frac{\text{i}}{{{\text{I}}_{\text{0}}}}
\right)}^{\text{2}}}\text{+}{{\left( \frac{\text{u}}{{{\text{U}}_{\text{0}}}}
\right)}^{\text{2}}}\text{=1}$
* Ví dụ minh họa
Dạng 1: Bài toán về thời gian dao động
Ví
dụ 1: Cho dòng điện xoay chiều i = $2$cos(100$\text{
}\!\!\pi\!\!\text{ }$t + $\text{ }\!\!\pi\!\!\text{ }$/6) (A)
a)
Tại t = 0,2 s, cường độ dòng điện có giá trị bao nhiêu, đang tăng hay giảm?
b)
Kể từ t = 0, dòng điện có độ lớn bằng giá trị hiệu dụng của nó lần thứ 2018 tại
thời điểm?
Hướng dẫn
a) Tại t = 0,2 s: i =
2cos(100$\text{ }\!\!\pi\!\!\text{ }$.0,2 + $\text{ }\!\!\pi\!\!\text{ }$/6) = $\sqrt{3}$(A)
b) |i|= $\frac{{{\text{I}}_{\text{0}}}}{\sqrt{\text{2}}}$:
t = $\frac{2016}{4}$T + $\frac{1}{24}$T + $\frac{1}{4}$T = $\frac{\text{12103}}{\text{24}}\text{.}\frac{\text{2
}\!\!\pi\!\!\text{ }}{\text{100 }\!\!\pi\!\!\text{ }}$= $10,09$(s)
Ví
dụ 2: Đặt vào hai đầu một ống điệp áp xoay chiều u = $220\sqrt{2}$cos(100$\text{
}\!\!\pi\!\!\text{ }$ - $\text{ }\!\!\pi\!\!\text{ }$/6) (V). Đèn chỉ sang nếu
điện áp 2 đầu đèn có độ lớn không nhỏ hơn $110\sqrt{2}$V
a)
Trong 1 chu kì, khoảng thời gian đèn sang/ tắt là?
b)
Kể từ lúc t = 0, thời điểm đèn tắt lần thứ 4030 là?
Hướng dẫn
T = $\frac{\text{2 }\!\!\pi\!\!\text{ }}{\text{
}\!\!\omega\!\!\text{ }}$ = 0,02 (s)
a) Trong 1 chu kì:
Thời gian đèn sáng: $\frac{\text{2T}}{\text{3}}$ =
$\frac{1}{75}$(s)
Thời gian đèn tắt: \[\frac{\text{T}}{\text{3}}\] =
$\frac{1}{150}$ (s)
b) Thời điểm đèn tắt lần
thứ 2018 là thời điềm u = -$\frac{{{\text{U}}_{\text{0}}}}{\text{2}}$ đang
tăng:
t = $\frac{4028}{2}$T + T - $\frac{\text{T}}{\text{4}}$
= $\frac{8059}{200}$ (s)
Dạng 2: Quan hệ tức thời các điện áp,
dòng điện
Ví
dụ 1: Đặt điệp áp xoay chiều vào hai đầu đoạn mạch AB
thấy ${{\text{u}}_{\text{AM}}}$ = 70cos(100$\text{ }\!\!\pi\!\!\text{ }$t - $\text{
}\!\!\pi\!\!\text{ }$/2) (V), ${{\text{u}}_{\text{MB}}}$ = 80cos(100$\text{
}\!\!\pi\!\!\text{ }$t - $\text{ }\!\!\pi\!\!\text{ }$/6) (V). Tính điện áp hiệu
dụng đặt vào 2 điểm AB.
Hướng dẫn
${{\text{u}}_{\text{AM}}}$ = ${{\text{u}}_{\text{AM}}}$
+ ${{\text{u}}_{\text{MB}}}$ = 70 $\angle $ -$\frac{\text{ }\!\!\pi\!\!\text{
}}{\text{2}}$ + 80 $\angle $-$\frac{\text{ }\!\!\pi\!\!\text{ }}{\text{6}}$ =
130 $\angle $ -0,1
$\Rightarrow $ ${{\text{U}}_{\text{0AB}}}$ = 130
(V) $\Rightarrow $ ${{\text{U}}_{\text{AB}}}$ = $\frac{130}{\sqrt{2}}$ = $65\sqrt{2}$(V)
Ví
dụ 2: Cho đoạn mạch xoay chiều không phân nhánh RLC, ${{\text{Z}}_{\text{L}}}$
= 2${{\text{Z}}_{\text{C}}}$. Tại một thời điểm, điện áp tức thời trên điện trở
và tụ điện lần lượt là 80 V và 50 V. Khi đó điện áp tức thời giữa 2 đầu tụ là
bao nhiêu?
Hướng dẫn
${{\text{Z}}_{\text{L}}}$ = 2${{\text{Z}}_{\text{C}}}$
$\Rightarrow $ ${{\text{u}}_{\text{L}}}$ = -2${{\text{u}}_{\text{C}}}$ = -100
(V)
u = ${{\text{u}}_{\text{R}}}$ + ${{\text{u}}_{\text{L}}}$
+ ${{\text{u}}_{\text{C}}}$ = 30 (V)
Ví
dụ 3: Đặt u = $220\sqrt{2}$cos100$\text{
}\!\!\pi\!\!\text{ }$t (V) vào hai đầu
đoạn mạch RLC với R = 20 $\Omega $, L = 0,8/$\text{ }\!\!\pi\!\!\text{ }$ H, C
= ${{10}^{-3}}$/6$\text{ }\!\!\pi\!\!\text{ }$ F. Khi điện áp tức thời giữa 2 đầu
điện trở là $110\sqrt{3}$ V thì điện áp tức thời giữa 2 đầu cuộn cảm có độ lớn
bao nhiêu?
Hướng dẫn
${{\text{Z}}_{\text{L}}}$ = $\text{
}\!\!\omega\!\!\text{ }$L = 80 ($\Omega $); ${{\text{Z}}_{\text{C}}}$ = $\frac{\text{1}}{\text{
}\!\!\omega\!\!\text{ C}}$ = 60 ($\Omega $)
$\Rightarrow $ Z = $\sqrt{{{\text{R}}^{\text{2}}}\text{+}{{\left(
{{\text{Z}}_{\text{L}}}\text{-}{{\text{Z}}_{\text{C}}} \right)}^{\text{2}}}}$ =
$20\sqrt{2}$ ($\Omega $)
${{\text{I}}_{\text{0}}}$ = $\frac{{{\text{U}}_{\text{0}}}}{\text{Z}}$
= 11 (A)
${{\text{U}}_{\text{0R}}}$ = ${{\text{I}}_{\text{0}}}$R
= 220 (V); ${{\text{U}}_{\text{0L}}}$ = ${{\text{I}}_{\text{0}}}{{\text{Z}}_{\text{L}}}$
= 880 (V)
${{\left(
\frac{{{\text{u}}_{\text{R}}}}{{{\text{U}}_{\text{0R}}}} \right)}^{\text{2}}}$
+ ${{\left( \frac{{{\text{u}}_{\text{L}}}}{{{\text{U}}_{\text{0L}}}}
\right)}^{\text{2}}}$ = 1 $\Rightarrow $ |${{\text{u}}_{\text{L}}}$| = 440 (V)
Ví
dụ 4: Đặt u = 100cos100$\text{ }\!\!\pi\!\!\text{ }$t
(V) vào hai đầu đoạn mạch R = 50 $\Omega $, L = 1/$\text{ }\!\!\pi\!\!\text{ }$
H, C = ${{10}^{-3}}$/5$\text{ }\!\!\pi\!\!\text{ }$ F. Tính ${{\text{u}}_{\text{R}}}$,
${{\text{u}}_{\text{L}}}$ và u khi điện áp tức thời giữa 2 đầu cuộn cảm là $50\sqrt{2}$
V và đang giảm.
Hướng dẫn
${{\text{Z}}_{\text{L}}}$ = $\text{
}\!\!\omega\!\!\text{ }$L = 100 ($\Omega $); ${{\text{Z}}_{\text{C}}}$ = $\frac{\text{1}}{\text{
}\!\!\omega\!\!\text{ C}}$ = 50 ($\Omega $)
$\Rightarrow $ Z = $\sqrt{{{\text{R}}^{\text{2}}}\text{+}{{\left(
{{\text{Z}}_{\text{L}}}\text{-}{{\text{Z}}_{\text{C}}} \right)}^{\text{2}}}}$ =
$50\sqrt{2}$ ($\Omega $)
${{\text{I}}_{\text{0}}}$ = $\frac{{{\text{U}}_{\text{0}}}}{\text{Z}}$
= $\sqrt{2}$ (A)
${{\text{U}}_{\text{0R}}}$ = ${{\text{I}}_{\text{0}}}$R
= $50\sqrt{2}$ (V); ${{\text{U}}_{\text{0L}}}$ = ${{\text{I}}_{\text{0}}}{{\text{Z}}_{\text{L}}}$
= $100\sqrt{2}$ (V)
${{\text{Z}}_{\text{L}}}$ = 2${{\text{Z}}_{\text{C}}}$
$\Rightarrow $ ${{\text{u}}_{\text{L}}}$ = -2${{\text{u}}_{\text{C}}}$ $\Rightarrow
$ ${{\text{u}}_{\text{C}}}$ = -$25\sqrt{2}$ (V)
${{\text{u}}_{\text{L}}}$ = $\frac{{{\text{U}}_{\text{0L}}}}{\text{2}}$
đang giảm $\Rightarrow $ \[{{\phi }_{{{\text{u}}_{\text{R}}}}}\] = \[\frac{\text{
}\!\!\pi\!\!\text{ }}{\text{3}}\text{-}\frac{\text{ }\!\!\pi\!\!\text{
}}{\text{2}}\] = $\text{-}\frac{\text{ }\!\!\pi\!\!\text{ }}{\text{6}}$ $\Rightarrow
$ ${{\text{u}}_{\text{R}}}$ = $\frac{{{\text{U}}_{\text{0R}}}\sqrt{\text{3}}}{\text{2}}$
= $25\sqrt{6}$ (V)
u = ${{\text{u}}_{\text{R}}}$+ ${{\text{u}}_{\text{L}}}$
+ ${{\text{u}}_{\text{C}}}$ = $25\sqrt{6}$ + $50\sqrt{2}$ - $25\sqrt{2}$ = $25\sqrt{6}$+
$25\sqrt{2}$ (V)
Ví
dụ 5: Đặt điện áp u = U$\sqrt{2}$cos$\text{
}\!\!\omega\!\!\text{ }$t (V) vào 2 đầu đoạn mạch RC thì thấy ${{\text{U}}_{\text{R}}}$
= $50\sqrt{2}$ V. Tại 1 thời điểm, điện áp tức thời hai đầu đoạn mạch và hai đầu
điện trở lần lượt là $100\sqrt{3}$ V và $50\sqrt{3}$ V. Xác định U.
Hướng dẫn
${{\text{u}}_{\text{C}}}$ = u - ${{\text{u}}_{\text{L}}}$
= $50\sqrt{3}$ (V)
${{\left(
\frac{{{\text{u}}_{\text{R}}}}{{{\text{U}}_{\text{0R}}}}
\right)}^{\text{2}}}\text{+}{{\left( \frac{{{\text{u}}_{\text{C}}}}{{{\text{U}}_{\text{0C}}}}
\right)}^{\text{2}}}$ = 1 $\Rightarrow $ ${{\text{U}}_{\text{0C}}}$ = $100\sqrt{3}$
(V)
U = $\frac{\sqrt{\text{U}_{\text{0R}}^{\text{2}}\text{+U}_{\text{0C}}^{\text{2}}}}{\sqrt{\text{2}}}$
= $100\sqrt{2}$ (V)
Ví
dụ 6: Đặt u = U$\sqrt{2}$cos$\text{
}\!\!\omega\!\!\text{ }$t (V) vào 2 đầu đoạn mạch RLC. Người ta thấy ${{\text{u}}_{\text{RL}}}$
và u lệch pha $\text{ }\!\!\pi\!\!\text{ }$/2. Tại một thời điểm nào đó, điện
áp tức thời giữa hai đầu tụ điện là $50\sqrt{6}$ V thì điện áp tức thời giữa RL
là $25\sqrt{6}$ V. ${{\text{U}}_{\text{R}}}$ = 75 V. Tính U.
Hướng dẫn
u = ${{\text{u}}_{\text{RL}}}$ + ${{\text{u}}_{\text{C}}}$
= $25\sqrt{6}$ + $50\sqrt{6}$ = $75\sqrt{6}$ (V)
${{\text{u}}_{\text{RL}}}$ $\bot $ u $\Rightarrow
$ ${{\left( \frac{{{\text{u}}_{\text{RL}}}}{{{\text{U}}_{\text{0RL}}}}
\right)}^{\text{2}}}\text{+}{{\left( \frac{\text{u}}{{{\text{U}}_{0}}}
\right)}^{\text{2}}}$ = 1 (1)
$\frac{\text{1}}{\text{U}_{\text{0R}}^{\text{2}}}$
= $\frac{\text{1}}{\text{U}_{\text{0RL}}^{\text{2}}}$ + $\frac{\text{1}}{\text{U}_{\text{0}}^{\text{2}}}$
(2)
Từ (1), (2) suy ra ${{\text{U}}_{\text{0}}}$ = $150\sqrt{2}$
(V) $\Rightarrow $ U = $\frac{{{\text{U}}_{\text{0}}}}{\sqrt{\text{2}}}$ = 150
(V)
Ví
dụ 7: Đặt vào hai đầu đoạn mạch chỉ có tụ điện có điện
dung 0,1/$\text{ }\!\!\pi\!\!\text{ }$ mF một điệp áp xoay chiều u = ${{\text{U}}_{\text{0}}}$cos100$\text{
}\!\!\pi\!\!\text{ }$t (V). Tính cường độ dòng điện tại thời điểm ${{\text{t}}_{\text{1}}}$
+ 0,005 (s) biết tại thời điểm ${{\text{t}}_{\text{1}}}$ điện áp là 50 V.
Hướng dẫn
${{\text{Z}}_{\text{C}}}$ = $\frac{\text{1}}{\text{
}\!\!\omega\!\!\text{ C}}$ = 100 ($\Omega $)
Cách 1: u = ${{\text{U}}_{\text{0}}}$cos100$\text{
}\!\!\pi\!\!\text{ }$t $\Rightarrow $ Tại ${{\text{t}}_{\text{1}}}$: 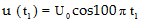 = 50
= 50
i = $\frac{{{\text{U}}_{\text{0}}}}{{{\text{Z}}_{\text{C}}}}$cos(100$\text{
}\!\!\pi\!\!\text{ }$t + $\text{ }\!\!\pi\!\!\text{ }$/2)
$\Rightarrow $ Tại ${{\text{t}}_{\text{1}}}$+
0,005: i (${{\text{t}}_{\text{1}}}$+ 0,005) = $\frac{{{\text{U}}_{\text{0}}}}{\text{100}}$cos[100$\text{
}\!\!\pi\!\!\text{ }$(${{\text{t}}_{\text{1}}}$+ 0,005) + $\text{
}\!\!\pi\!\!\text{ }$/2] = $\frac{\text{-}{{\text{U}}_{\text{0}}}\text{cos100
}\!\!\pi\!\!\text{ }{{\text{t}}_{\text{1}}}}{\text{100}}$ = - 0,5 (A)
Cách 2: Vì ${{\text{t}}_{\text{2}}}$ - ${{\text{t}}_{\text{1}}}$ = 0,005 = $\frac{\text{T}}{\text{4}}$ $\Rightarrow $ ${{\text{i}}_{\text{2}}}$ = -$\frac{{{\text{u}}_{\text{1}}}}{{{\text{Z}}_{\text{C}}}}$ = -$\frac{50}{100}$ = - 0,5 (A)
* Bài tập tự luyện
Bài 1: Dòng điện xoay
chiều có cường độ i = $\text{4}\sqrt{\text{2}}\text{cos}\left( \text{120
}\!\!\pi\!\!\text{ t+}\frac{\text{ }\!\!\pi\!\!\text{ }}{\text{3}} \right)$
(A). Ở thời điểm t = $\frac{1}{90}$ s, cường độ tức thời của dòng điện này có
giá trị
A. cực đại B. $2\sqrt{2}$ và đang giảm
C. cực tiểu D. $2\sqrt{2}$ và đang tăng
Bài 2: Cho dòng điện
xoay chiều có tần số 50 Hz chạy qua một đoạn mạch. Khoảng thời gian giữa hai lần
liên tiếp cường độ dòng điện này bằng 0 là
A. $\frac{1}{100}$ s B. $\frac{1}{200}$
s C. $\frac{1}{50}$
s D. $\frac{1}{25}$
s
Bài 3: Cho một dòng
điện xoay chiều có cường độ i = 4sin100$\text{ }\!\!\pi\!\!\text{ }$t (A), t
tính bằng giây. Tại thời điểm ${{\text{t}}_{\text{0}}}$, giá trị của i là $2\sqrt{3}$
A và đang tăng. Đến thời điểm sau đó 0,045 s thì giá trị của i là
A. - 4 A B. $2\sqrt{3}$ và đang tăng
C. – 2 A và đang giảm D. 2 A và đang giảm
Bài 4: Đặt điện áp u
= 310cos100$\text{ }\!\!\pi\!\!\text{ }$t (V) (t tính bằng giây) vào hai đầu một
đoạn mạch. Kể từ thời điểm t = 0, điện áp tức thời giữa hai đầu đoạn mạch này đạt
giá trị 155 V lần đầu tiên tại thời điểm
A. $\frac{1}{120}$ s B. $\frac{1}{300}$
s C. $\frac{1}{60}$
s D. $\frac{1}{600}$
s
Bài 5: Một dòng điện
có cường độ i = ${{\text{I}}_{\text{0}}}$cos$\text{ }\!\!\pi\!\!\text{ }$ft. Tính
từ t = 0, khoảng thời gian ngắn nhất để cường độ dòng điện này bằng 0 là 0,004
s. Giá trị của f bằng
A. 62,5 Hz B. 60 Hz C. 52,5
Hz D. 50 Hz
Bài 6: Biểu thức hiệu
điện thế hai đầu một đoạn mạch u = 200cos$\text{ }\!\!\omega\!\!\text{ }$t (V).
Tại thời điểm t, điện áp u = 100 V và đang tăng. Hỏi vào thời điểm t’ = t + $\frac{\text{T}}{\text{4}}$
điện áp u có giá trị bằng bao nhiêu?
A. 100 V B. $100\sqrt{2}$
V C. $100\sqrt{3}$
V D. -100 V
Bài 7: Mắc vào đèn
neon một nguồn điện xoay chiều có biểu thức u = $220\sqrt{2}$cos(100$\text{
}\!\!\pi\!\!\text{ }$t - $\text{ }\!\!\pi\!\!\text{ }$/2) (V). Đèn chỉ sáng khi
điện áp đặt vào đèn thoả mãn |u| $\ge $ $110\sqrt{2}$ V. Tỉ số khoảng thời gian
thời gian đèn sáng so với đèn tắt trong một chu kì của dòng điện bằng
A. 2 B. $\frac{1}{2}$
C. $\frac{2}{3}$
D. $\frac{3}{2}$
Bài 8: Một chiếc đèn
nêôn đặt dưới một điện áp xoay chiều 119 V – 50 Hz. Nó chỉ sáng lên khi điện áp
tức thời giữa hai đầu bóng đèn lớn hơn 84 V. Thời gian bóng đèn sáng trong một
chu kỳ là bao nhiêu?
A. 0,0100 s B. 0,0133 s C. 0,0200 s D. 0,0233 s
Bài 9: Điện áp giữa
hai đầu một đoạn mạch là u = 150 cos100$\text{ }\!\!\pi\!\!\text{ }$t (V). Cứ mỗi
giây có bao nhiêu lần điện áp này bằng không?
A. 100 lần B. 50 lần C. 200 lần D. 2 lần
Bài 10: Dòng điện
xoay chiều qua một đoạn mạch có biểu thức i = ${{\text{I}}_{\text{0}}}$cos(120$\text{
}\!\!\pi\!\!\text{ }$t - $\text{ }\!\!\pi\!\!\text{ }$/3) (A). Thời điểm thứ
2018 độ lớn cường độ dòng điện bằng cường độ dòng điện hiệu dụng là:
A. 8,15 s B. 8,4 s C. 9,26 s
D. 10,3 s
Bài 11: Một đèn ống mắc
trong mạch điện xoay chiều có điện áp u = ${{\text{U}}_{\text{0}}}$cos(100$\text{
}\!\!\pi\!\!\text{ }$t) (V). Đèn chỉ sáng khi điện áp ở 2 cực của nó có độ lớn
không nhỏ hơn 0,5${{\text{U}}_{\text{0}}}$. Một máy ghi hình với tốc độ 24
hình/s ghi lại thấy rằng: trong 3 s số tấm hình cho thấy đèn ống không sáng (tối)
là
A. 24 B. 30 C. 50 D. 100
Bài 12: Đặt vào hai đầu
đèn ống điện áp xoay chiều u = 250cos(100$\text{ }\!\!\pi\!\!\text{ }$t + $\text{
}\!\!\pi\!\!\text{ }$) (V). Biết đèn chỉ sáng khi điện áp tức thời có độ lớn
không nhỏ hơn $125\sqrt{2}$ V. Kể từ t = 0, thời điểm đèn tắt lần thứ 2016 là
A. 20,1525 s B. 10,0675 s C. 20,1475 s D.
10,0725 s
Bài 13: Một đoạn mạch
AB gồm điện trở thuần, cuộn cảm và tụ điện mắc nối tiếp. M là một điểm trên đoạn
mạch AB. Điện áp ${{\text{u}}_{\text{AM}}}$ = 100cos100$\text{
}\!\!\pi\!\!\text{ }$t (V) và ${{\text{u}}_{\text{MB}}}$ = $100\sqrt{3}$cos(100$\text{
}\!\!\pi\!\!\text{ }$t - $\text{ }\!\!\pi\!\!\text{ }$/2) (V). Điện áp giữa hai
đầu đoạn mạch AB là
A. ${{\text{u}}_{\text{AB}}}$
= 200cos(100$\text{ }\!\!\pi\!\!\text{ }$t + $\text{ }\!\!\pi\!\!\text{ }$/6)
(V) B. ${{\text{u}}_{\text{AB}}}$
= 200cos(100$\text{ }\!\!\pi\!\!\text{ }$t - $\text{ }\!\!\pi\!\!\text{ }$/6)
(V)
C. ${{\text{u}}_{\text{AB}}}$
= 200cos(100$\text{ }\!\!\pi\!\!\text{ }$t + $\text{ }\!\!\pi\!\!\text{ }$/3)
(V) D. ${{\text{u}}_{\text{AB}}}$
= 200cos(100$\text{ }\!\!\pi\!\!\text{ }$t - $\text{ }\!\!\pi\!\!\text{ }$/3)
(V)
Bài 14: Mạch điện
xoay chiều không phân nhánh gồm điện trở thuần R, cuộn cảm thuần có cảm kháng ${{\text{Z}}_{\text{L}}}$
và tụ điện có dung kháng ${{\text{Z}}_{\text{C}}}$ = 2${{\text{Z}}_{\text{L}}}$.
Vào một thời điểm khi hiệu điện thế trên điện trở và trên tụ điện có giá trị tức
thời tương ứng là 40V và 30V thì hiệu điện thế giữa hai đầu mạch điện là:
A. 50V B. 85V C. 25V D. 55V
Bài 15: Đặt điện áp u
= $220\sqrt{2}$cos100$\text{ }\!\!\pi\!\!\text{ }$t (V) vào hai đầu đoạn mạch mắc
nối tiếp gồm điện trở 20 $\Omega $, cuộn cảm có độ tự cảm 0,8/$\text{
}\!\!\pi\!\!\text{ }$ H và tụ điện có điện dung ${{10}^{-3}}$/6$\text{
}\!\!\pi\!\!\text{ }$ F. Khi điện áp tức thời giữa hai đầu điện trở bằng $110\sqrt{3}$
V thì điện áp tức thời giữa hai đầu cuộn cảm có độ lớn bằng:
A. 440V B. 330V C C. $440\sqrt{3}$ V D. $330\sqrt{3}$
Bài 16: Đặt điện áp
xoay chiều vào hai đầu đoạn mạch gồm điện trở thuần, cuộn cảm thuần và tụ điện
mắc nối tiếp. Biết cảm kháng của cuộn cảm bằng 4 lần dung kháng của tụ điện. Tại
thời điểm t, điện áp tức thời giữa hai đầu tụ điện có giá trị cực đại là 50 V
thì điện áp tức thời giữa hai đầu đoạn mạch là
A. 150 V B. -150 V C. 200 V D. -200 V
Bài 17: Đoạn mạch
xoay chiều RLC mắc nối tiếp. Điện áp hiệu dụng ở hai đầu điện trở, hai đầu cuộn
cảm thuần và hai đầu tụ điện lần lượt là $30\sqrt{2}$ V, $60\sqrt{2}$ V và $90\sqrt{2}$
V. Khi điện áp tức thời ở hai đầu điện trở là 30V thì điện áp tức thời ở hai đầu
mạch có thể là
A. 42,43 V B. 81,96 V C. 60 V D. 90 V
Bài 18: Đặt điện áp
xoay chiều có tần số ω vào hai đầu đoạn mạch gồm điện trở thuần, cuộn cảm thuần
có độ tự cảm L và tụ điện có điện dung C mắc nối tiếp. Biết 2LC${{\text{
}\!\!\omega\!\!\text{ }}^{\text{2}}}$ = 1. Tại thời điểm t, điện áp tức thời giữa
hai đầu điện trở và hai đầu tụ điện lần lượt là 40V và 60V. Khi đó điện áp tức
thời giữa hai đầu đoạn mạch là
A. 50 V B. 55 V C.
70 V D. 100 V
Bài 19: Một đoạn mạch điện gồm điện trở R = $50\sqrt{3}$
$\Omega $ mắc nối tiếp với cuộn thuần cảm có L = 1/2$\text{ }\!\!\pi\!\!\text{
}$ H. Đặt vào hai đầu đoạn mạch một điện áp xoay chiều có giá trị hiệu dụng 200
V, tần số 50 Hz. Tại thời điểm t, cường độ dòng điện qua mạch có giá trị bằng $\sqrt{2}$
và đang tăng thì điện áp hai đầu mạch sau đó 1/300 s bằng
A. $100\sqrt{2}$ V B. 0 V C. $100\sqrt{6}$
V D. -$100\sqrt{6}$
V
Bài 20: Đặt một điện áp xoay chiều u vào hai đầu của một đoạn mạch gồm điện trở R mắc nối tiếp với một tụ điện có điện dung C. Điện áp tức thời hai đầu điện trở R có biểu thức ${{\text{u}}_{\text{R}}}$ = 100cos(2$\text{ }\!\!\pi\!\!\text{ }$ft + $\text{ }\!\!\varphi\!\!\text{ }$) (V). Vào một thời điểm t nào đó điện áp tức thời giữa hai đầu đoạn mạch và hai đầu điện trở có giá trị u = $100\sqrt{3}$ V và ${{\text{u}}_{\text{R}}}$= $50\sqrt{3}$ V. Điện áp hiệu dụng giữa hai dầu tụ điện
A. $50\sqrt{3}$ V B. $50\sqrt{6}$ V C. 50 V D. $100\sqrt{3}$ V
Bài 21: Đặt vào điện
áp u = $120\sqrt{2}$cos100$\text{ }\!\!\pi\!\!\text{ }$t (V) vào hai đầu đoạn mạch
gồm điện trở R và tụ điện mắc nối tiếp với ${{\text{Z}}_{\text{C}}}$ = $\frac{\text{R}}{\sqrt{\text{3}}}$.
Tại thời điểm t = $\frac{1}{150}$ s thì hiệu điện thế trên tụ có giá trị bằng
A. $30\sqrt{6}$ V B. $30\sqrt{2}$
V C. $60\sqrt{2}$
V D. $60\sqrt{6}$
V
Bài 22: Đặt điện áp
xoay chiều u = ${{\text{U}}_{\text{0}}}$ cos100$\text{ }\!\!\pi\!\!\text{ }$t
(V) vào hai đầu đoạn mạch nối tiếp gồm điện trở thuần R = $100\sqrt{3}$ $\Omega
$, cuộn cảm thuần có độ tự cảm L = 2/$\text{ }\!\!\pi\!\!\text{ }$ H và tụ điện
có điện dung C = 100/$\text{ }\!\!\pi\!\!\text{ }$ $\text{ }\!\!\mu\!\!\text{
F}$. Tại thời điểm khi điện áp tức thời giữa hai đầu đoạn mạch có giá trị bằng
một nửa giá trị cực đại thì cường độ dòng điện tức thời trong mạch i = $0,5\sqrt{3}$
A. Dùng vôn kế nhiệt có điện trở rất lớn để đo hiệu điện thế hai đầu tụ điện
thì vôn kế chỉ:
A. 200V B. 100 V C. $100\sqrt{2}$
V D. $50\sqrt{2}$
V
Bài 23: Đặt điện áp
xoay chiều u = ${{\text{U}}_{\text{0}}}$cos$\text{ }\!\!\omega\!\!\text{ }$t vào
hai đầu đoạn mạch gồm điện trở thuần R và cuộn cảm thuần có cảm kháng ${{\text{Z}}_{\text{L}}}$
mắc nối tiếp. Gọi U là điện áp hiệu dụng giữa hai đầu đoạn mạch; i, ${{\text{I}}_{\text{0}}}$
và I lần lượt là giá trị tức thời, giá trị cực đại và giá trị hiệu dụng của cường
độ dòng điện trong đoạn mạch; ${{\text{u}}_{\text{L}}}$, ${{\text{u}}_{\text{R}}}$
tương ứng là điện áp tức thời giữa hai đầu cuộn cảm, giữa hai đầu điện trở, cos$\text{
}\!\!\varphi\!\!\text{ }$ là hệ số công suất của đoạn mạch. Hệ thức nào sau đây
sai?
A. ${{\left(
\frac{{{\text{u}}_{\text{L}}}}{{{\text{Z}}_{\text{L}}}} \right)}^{\text{2}}}$ +
${{\left( \frac{{{\text{u}}_{\text{R}}}}{\text{R}} \right)}^{\text{2}}}$ = 1 B. I = $\frac{{{\text{U}}_{\text{0}}}}{\sqrt{\text{2}\left(
{{\text{R}}^{\text{2}}}\text{+Z}_{\text{L}}^{\text{2}} \right)}}$
C. cos$\text{
}\!\!\varphi\!\!\text{ }$ = $\frac{\text{R}}{\sqrt{{{\text{R}}^{\text{2}}}\text{+Z}_{\text{L}}^{\text{2}}}}$
D. $\text{u}_{\text{L}}^{\text{2}}$
+ ${{\text{i}}^{\text{2}}}\text{Z}_{\text{L}}^{\text{2}}$ = $\text{I}_{\text{0}}^{\text{2}}\text{Z}_{\text{L}}^{\text{2}}$
Bài 24: Đặt điện áp u
= 120cos100$\text{ }\!\!\pi\!\!\text{ }$t (V) vào hai đầu đoạn mạch gồm điện trở
thuần R = 60 $\text{ }\!\!\Omega\!\!\text{ }$, cuộn cảm thuần có độ tự cảm L =
8/5$\text{ }\!\!\pi\!\!\text{ }$ H, tụ điện có điện dung C = ${{10}^{-4}}$/$\text{
}\!\!\pi\!\!\text{ }$ F mắc nối tiếp. Ở thời điểm t = 30 ms cường độ dòng điện
trong mạch có giá trị là
A. -$\sqrt{2}$ A B. -1 A C. 1 A D. $\sqrt{2}$ A
Bài 25: Đặt điện áp u
= ${{\text{U}}_{\text{0}}}$cos100$\text{ }\!\!\pi\!\!\text{ }$t (V) vào hai đầu
đoạn mạch gồm cuộn dây có độ tự cảm L = 0,15/$\text{ }\!\!\pi\!\!\text{ }$ H và
điện trở r = $5\sqrt{3}$ $\Omega $, và tụ điện có điện dung C = ${{10}^{-3}}$/$\text{
}\!\!\pi\!\!\text{ }$ F mắc nối tiếp. Tại thời điểm ${{\text{t}}_{1}}$, Tại thời
điểm t1 điện áp tức thời hai đầu cuộn dây có giá trị 15 V, đến thời điểm ${{\text{t}}_{\text{2}}}$
= ${{\text{t}}_{1}}$ + 1/75 s thì điện áp tức thời hai đầu tụ điện cũng có giá
trị là 15 V. Giá trị của ${{\text{U}}_{\text{0}}}$ là
A. 15 V B. 30 V C. $15\sqrt{3}$
V D. $10\sqrt{3}$
V
Bài 26: Cho một đoạn
mạch điện xoay chiều có tần số 50 Hz, chỉ có cuộn cảm thuần với cảm kháng là 50
Ω. Tại thời điểm ${{\text{t}}_{1}}$ cường độ dòng điện qua mạch là – 1 A, hỏi
sau đó 0,015 s thì điện áp hai đầu cuộn cảm bằng
A. – 50 V B. 50 V C. – 100
V D. 100 V
Bài 27: Đặt một điện
áp xoay chiều có giá trị hiệu dụng là U vào hai đầu đoạn mạch RL mắc nối tiếp,
cuộn cảm thuần. Biết điện trở có giá trị gấp 3 lần cảm kháng. Gọi ${{\text{u}}_{\text{R}}}$
và ${{\text{u}}_{\text{L}}}$ lần lượt là điện áp tức thời ở hai đầu điện trở R
và ở hai đầu cuộn cảm thuần ở cùng một thời điểm. Hệ thức đúng là
A. 90$\text{u}_{\text{R}}^{\text{2}}$
+ 10$\text{u}_{\text{L}}^{\text{2}}$ = 9${{\text{U}}^{\text{2}}}$ B. 45$\text{u}_{\text{R}}^{\text{2}}$
+ 5$\text{u}_{\text{L}}^{\text{2}}$ = 9${{\text{U}}^{\text{2}}}$
C. 5$\text{u}_{\text{R}}^{\text{2}}$
+ 45$\text{u}_{\text{L}}^{\text{2}}$ = 9${{\text{U}}^{\text{2}}}$ D. 10$\text{u}_{\text{R}}^{\text{2}}$
+ 10$\text{u}_{\text{L}}^{\text{2}}$ = 9${{\text{U}}^{\text{2}}}$
Bài 28: Đặt một điện
áp xoay chiều vào hai đầu đoạn mạch RLC (L thuần cảm) nối tiếp. Biết điện áp
hai đầu đoạn mạch lệch pha so với cường độ dòng điện trong mạch là $\text{
}\!\!\varphi\!\!\text{ }$. Ở thời điểm t bất kì, điện áp tức thời trên đoạn mạch
chứa LC và trên R lần lượt là ${{\text{u}}_{\text{LC}}}$ và ${{\text{u}}_{\text{R}}}$.
Điện áp cực đại trên điện trở R là
A. ${{\text{U}}_{\text{0R}}}$
= ${{\text{u}}_{\text{LC}}}$cos$\text{ }\!\!\varphi\!\!\text{ }$+ ${{\text{u}}_{\text{R}}}$sin$\text{
}\!\!\varphi\!\!\text{ }$ B. ${{\text{U}}_{\text{0R}}}$ = ${{\text{u}}_{\text{LC}}}$sin$\text{
}\!\!\varphi\!\!\text{ }$+ ${{\text{u}}_{\text{R}}}$cos$\text{
}\!\!\varphi\!\!\text{ }$
C. $\text{U}_{\text{0R}}^{\text{2}}$
= $\text{u}_{\text{LC}}^{\text{2}}$ + ${{\left(
\frac{{{\text{u}}_{\text{R}}}}{\text{tan }\!\!\varphi\!\!\text{ }}
\right)}^{\text{2}}}$ D. $\text{U}_{\text{0R}}^{\text{2}}$
= $\text{u}_{\text{R}}^{\text{2}}$ + ${{\left(
\frac{{{\text{u}}_{\text{LC}}}}{\text{tan }\!\!\varphi\!\!\text{ }}
\right)}^{\text{2}}}$
Bài 29: Đặt
một điện áp xoay chiều ổn định vào hai đầu đoạn mạch nối tiếp gồm điện trở thuần
R ; cuộn cảm thuần và tụ điện. Tại thời điểm ${{\text{t}}_{\text{1}}}$ các giá
trị tức thời của điện áp hai đầu cuộn dây và hai đầu điện trở R lần lượt là ${{\text{u}}_{\text{L}}}$=
-$20\sqrt{3}$ V, ${{\text{u}}_{\text{R}}}$ = 30 V. Tại thời điểm ${{\text{t}}_{\text{2}}}$
các giá trị tức thời ${{\text{u}}_{\text{L}}}\text{ }\!\!'\!\!\text{ }$ = 40 V,
${{\text{u}}_{\text{C}}}\text{ }\!\!'\!\!\text{ }$ = -120 v, ${{\text{u}}_{\text{R}}}'$
= 0. Điện áp cực đại giữa hai đầu đoạn mạch là
A. 100 V B. 120 V C. $80\sqrt{3}$
V D. 60 V
Bài 30: Mạch
điện xoay chiều AB mắc nối tiếp theo thức tự gồm điện trở thuần, cuộn thuần cảm
và tụ điện. M là điểm nối giữa cuộn cảm thuần và tụ điện. Điện áp giữa hai đầu
AM luôn vuông pha với điện áp giữa hai đầu đoạn mạch. Điện áp cực đại trên điện
trở là 12a. Khi điện áp tức thời hai đầu đoạn mạch là 16a thì điện áp tức thời
trên tụ là 7a. Chọn hệ thức đúng
A. 4R = 3$\text{
}\!\!\omega\!\!\text{ }$L B. 3R = 4$\text{ }\!\!\omega\!\!\text{ }$L C. R = 2$\text{
}\!\!\omega\!\!\text{ }$L D. 2R = $\text{ }\!\!\omega\!\!\text{ }$L
Bài 31: Mạch điện
xoay chiều mắc nối tiếp gồm điện trở thuần R và tụ điện có điện dung C mắc nối
tiếp. Dung kháng tụ điện trong mạch là 50 $\Omega $. Biết tại thời điểm t bất
kì, điện áp tức thời giữa hai đầu điện trở là ${{\text{u}}_{\text{R}}}$ (V) thì
điện áp tức thời giữa hai đầu tụ điện là ${{\text{u}}_{\text{C}}}$ (V) luôn thỏa
mãn 9$\text{u}_{\text{C}}^{\text{2}}$ + 4$\text{u}_{\text{R}}^{\text{2}}$ = c,
c là một hằng số. Điện trở R có giá trị:
A. 60 $\Omega $ B. 75 V C. 40 $\Omega
$ D. 50 $\Omega
$
Bài 32: Đoạn mạch
xoay chiều AB chứa 3 linh kiện R, L, C. Đoạn AM chứa L, MN chứa R, NB chứa C, R
= 50 $\Omega $, ${{\text{Z}}_{\text{L}}}$ = $50\sqrt{3}$ $\Omega $, ${{\text{Z}}_{\text{C}}}$
= 50/$\sqrt{3}$ $\Omega $. Khi ${{\text{u}}_{\text{AN}}}$ = $80\sqrt{3}$ V thì ${{\text{u}}_{\text{MB}}}$
= 60 V. Giá trị cực đại điện áp giữa hai đầu đoạn mạch là
A. 150 V B. 100 V C. $50\sqrt{7}$
V D. $100\sqrt{3}$
V
Bài 33: Đặt điện áp
xoay chiều u = $100\sqrt{2}$cos100$\text{ }\!\!\pi\!\!\text{ }$t (V) vào hai đầu
đoạn mạch RL mắc nối tiếp. Biết điệp áp hiệu dụng giữa hai đầu cuộn cảm thuần
là 60 V. Tại thời điểm ${{\text{t}}_{\text{1}}}$, điện áp hai đầu cuộn cảm là $30\sqrt{2}$
V và đang giảm. Tại thời điểm ${{\text{t}}_{\text{2}}}$ = ${{\text{t}}_{\text{1}}}$
+ 1/600 s, điện áp giữa hai đầu điện trở có giá trị là
A. 80 V B. -$40\sqrt{2}$
V C. $40\sqrt{3}$ V D. $80\sqrt{2}$
V
* Đáp án
|
1 D |
2 A |
3 D |
4 B |
5 A |
6 C |
7 A |
8 B |
9 A |
10 B |
|
11 A |
12 A |
13 D |
14 D |
15 A |
16 B |
17 B |
18 C |
19 C |
20 B |
|
21 B |
22 D |
23 A |
24 B |
25 D |
26 A |
27 C |
28 D |
29 A |
30 B |
|
31 B |
32 C |
33 D |
|
|
|
|
|
|
|







