1. Ứng dụng bất đẳng thức để giải phương trình
Ví dụ 1:
Giải phương trình: \[\left| x-5 \right|+\left| x-2 \right|=3\]
Giải.
áp dụng BĐT \[\left| x \right|+\left| y \right|\ge \left| x+y \right|\] . Ta có:
\[\left| x-5 \right|+\left| x-2 \right|=\left| x-5 \right|+\left| 2-x \right|=\left| x-5+2-x \right|=3.\]
Dấu “=” xảy ra khi và chỉ khi \[\left( x5 \right)\left( 2-x \right){}^\text{3}\text{ =}0\]hay \[2\le x\le 5\]
Vậy phương trình có nghiệm với mọi x thoả mãn \[2\le x\le 5\]
Ví dụ 2:
Giải phương trình: \[\sqrt{3{{x}^{2}}+6x+7}+\sqrt{5{{x}^{2}}+10x+14}=4-2x-{{x}^{2}}\]
Giải:
Ta có : \[\sqrt{3{{x}^{2}}+6x+7}=\sqrt{3\left( {{x}^{2}}+2x+1 \right)+4}=\sqrt{3{{\left( x+1 \right)}^{2}}+4}\ge 2\]
\[\sqrt{5{{x}^{2}}+10x+14}=\sqrt{5\left( {{x}^{2}}+2x+1 \right)+9}=\sqrt{5{{\left( x+1 \right)}^{2}}+9}\ge 3\]
Suy ra: Vế trái = \[\sqrt{3{{x}^{2}}+6x+7}+\sqrt{5{{x}^{2}}+10x+14}\ge 5\]
Dấu “=” xảy ra khi và chỉ khi x = -1.
mà Vế phải = \[4-2x-{{x}^{2}}=-{{\left( x+1 \right)}^{2}}+5\le 5.\]
Dấu “=” xảy ra khi và chỉ khi x = -1
Vậy phương trình có nghiệm x = -1
2. Ứng dụng bất đẳng thức để tìm GTLN, GTNN
Ví dụ 1
Cho a , b, c là 3 số dương có tổng bằng 1. Tìm giá trị lớn nhất của biểu thức.
\[A=\sqrt{a+1}+\sqrt{b+1}+\sqrt{c+1}\]
Giải:
*Cách 1: Dùng BĐT Bunhiacôpxki
Ta có \[{{A}^{2}}={{\left( \sqrt{a+1}+\sqrt{b+1}+\sqrt{c+1} \right)}^{2}}\le \left( {{1}^{2}}+{{1}^{2}}+{{1}^{2}} \right)\left( a+1+b+1+c+1 \right)=12\]
mà A > 0. Suy ra \[A=\sqrt{12}=2\sqrt{3}.\] Dấu “=” xảy ra khi và chỉ khi \[a=b=c=\frac{1}{3}\]
* Cách 2: Dùng điểm rơi Côsi
Ta có: \[\sqrt{a+1}=\frac{\sqrt{3}}{2}\sqrt{\left( a+1 \right)\frac{4}{3}}\ge \frac{\sqrt{3}}{2}\left( \frac{a+1+\frac{4}{3}}{2} \right)=\frac{\sqrt{3}}{12}\left( 3a+7 \right)\]
Tương tự: \[\sqrt{b+1}\ge \frac{\sqrt{3}}{12}\left( 3b+7 \right);\sqrt{c+1}\ge \frac{\sqrt{3}}{12}\left( 3c+7 \right)\]
Suy ra: \[\sqrt{a+1}+\sqrt{b+1}+\sqrt{c+1}\ge \frac{\sqrt{3}}{12}\left( 3\left( a+b+c \right)+21 \right)=2\sqrt{3}\]
Dấu bằng xảy ra khi và chỉ khi \[a=b=c=\frac{1}{3}\]
Ví dụ 2. Cho a, b, c là số đo ba cạnh của một tam giác. Xác định hình dạng của tam giác để
\[A=\frac{a}{b+c}+\frac{b}{c+a}+\frac{c}{a+b}\] đạt giá trị nhỏ nhất
Giải.
Ta có: \[A=\frac{a}{b+c}+\frac{b}{c+a}+\frac{c}{a+b}=\left( \frac{a}{b+c}+1 \right)+\left( \frac{b}{c+a}+1 \right)+\left( \frac{c}{a+b}+1 \right)-3\]
=\[(a+b+c)\left( \frac{1}{b+c}+\frac{1}{c+a}+\frac{1}{a+b} \right)-3\]
= \[\frac{1}{2}\left[ \left( b+c \right)+(c+a)+(a+b) \right]\left( \frac{1}{b+c}+\frac{1}{c+a}+\frac{1}{a+b} \right)-3\]
Vì \[\frac{1}{2}\left[ \left( b+c \right)+(c+a)+(a+b) \right]\left( \frac{1}{b+c}+\frac{1}{c+a}+\frac{1}{a+b} \right)\ge \frac{1}{2}.9\]
Suy ra \[A=\frac{a}{b+c}+\frac{b}{c+a}+\frac{c}{a+b}\ge \frac{3}{2}\]. Dấu bằng xảy ra khi a=b=c.
Vậy \[A=\frac{a}{b+c}+\frac{b}{c+a}+\frac{c}{a+b}\] đạt giá trị lớn nhất khi a, b, c là ba cạnh của tam giác đều.
2) Cho a, b, c là số đo ba cạnh của một tam giác. Xác định hình dạng của tam giác để
\[\left( 1+\frac{b}{a} \right)\left( 1+\frac{c}{b} \right)\left( 1+\frac{a}{c} \right)=8\]
Giải.
Xét biểu thức \[B=\left( 1+\frac{b}{a} \right)\left( 1+\frac{c}{b} \right)\left( 1+\frac{a}{c} \right)=\left( \frac{a+b}{a} \right)\left( \frac{b+c}{b} \right)\left( \frac{c+a}{c} \right)\]
= \[\frac{(a+b)(b+c)(c+a)}{abc}\ge 8\]
Theo BĐT Cosi cho hai số dương ta có:
\[a+b\ge 2\sqrt{ab};\] \[a+c\ge 2\sqrt{ac};\] \[b+c\ge 2\sqrt{bc};\]
Suy ra \[(a+b)(b+c)(c+a)\ge 8abc\]
Nên \[\frac{(a+b)(b+c)(c+a)}{abc}\ge 8\] hay \[\left( 1+\frac{b}{a} \right)\left( 1+\frac{c}{b} \right)\left( 1+\frac{a}{c} \right)\ge 8\]
Dấu bằng xảy ra khi a=b=c.
Vậy a, b, c là ba cạnh của tam giác đều thì \[\left( 1+\frac{b}{a} \right)\left( 1+\frac{c}{b} \right)\left( 1+\frac{a}{c} \right)=8\]
3) Ứng dụng bất đẳng thức để chứng minh phương trình bậc hai có nhiệm, có hai nghiệm phân biệt.
Ví dụ 1: Cho phương trình: x2 + 2mx + (m – 1) = 0 với m là tham số
Chứng minh rằng phương trình luôn có hai nghiệm phân biệt
Giải.
Ta có \[\vartriangle '={{m}^{2}}-(m-1)\]
=\[{{m}^{2}}-m+1\]
=\[{{\left( m-\frac{1}{2} \right)}^{2}}-\frac{3}{4}>0\] với mọi giá trị của m.
Vậy phương trình đã cho có 2 nghiệm phân biệt với mọi giá trị của m.
Ví dụ 2. Cho a, b, c là ba số khác không, chứng minh rằng trong ban phương trình sau
\[a{{x}^{2}}+2bx+c=0~~~~\] (1)
\[b{{x}^{2}}+2cx+a=0~~~~\] (2)
\[c{{x}^{2}}+2ax+b=0~~~\] (3)
Có ít nhất một phương trình có nghiệm
Giải.
Ta có
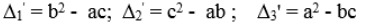
Suy ra
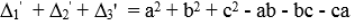
=\[\frac{{{(a+b)}^{2}}+{{(b+c)}^{2}}+{{(c+a)}^{2}}}{2}\ge 0\]
Từ đó suy ra phải có ít nhất một trong ba phương trình có ít nhất một nghiệm.







