1. Phương pháp 1: Biến đổi tương đương
Bài toán: Giải phương trình sau
\[\sqrt{{{x}^{2}}+5x+\sqrt{{{x}^{3}}+2x+1}}=x+1\]
ĐK: \[{{x}^{3}}+2x+1\ge 0\]; \[{{x}^{2}}+5x+\sqrt{{{x}^{3}}+2x+1}\ge 0\];
\[\sqrt{{{x}^{2}}+5x+\sqrt{{{x}^{3}}+2x+1}}=x+1\]
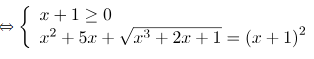
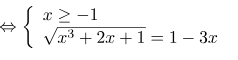
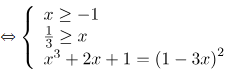
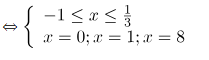
\[\Leftrightarrow x=0\] ( thỏa mãn điều kiện)
2. Phương pháp 2: Đặt ẩn số phụ
Bài toán: Giải phương trình: \[x\sqrt[3]{35-{{x}^{3}}}(x+\sqrt[3]{35-{{x}^{3}}})=30\]
Đặt \[t=x+\sqrt[3]{35-{{x}^{3}}}\Rightarrow x\sqrt[3]{35-{{x}^{3}}}=\frac{{{t}^{3}}-35}{3t}\]
Phương trình đã cho trở thành:
\[\frac{{{t}^{3}}-35}{3t}.t=30\Leftrightarrow {{t}^{3}}=125\Leftrightarrow t=5\Leftrightarrow x\sqrt[3]{35-{{x}^{3}}}=6\Leftrightarrow {{x}^{3}}(35-{{x}^{3}})=216\]
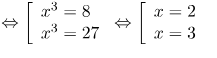
3. Phương pháp 3: Phương pháp làm xuất hiện biểu thức liên hợp
Bài toán: Giải phương trình: \[\left( \sqrt{x-1}+\sqrt{x+2} \right)(\sqrt{{{x}^{2}}+x-2}-1)=3\]
Đk: \[x\ge 1\]
\[\left( \sqrt{x-1}+\sqrt{x+2} \right)(\sqrt{{{x}^{2}}+x-2}-1)=3\]
\[\Leftrightarrow \left[ \left( x+2 \right)-(x-1) \right]\left( \sqrt{{{x}^{2}}+x-2}-1 \right)=3(-\sqrt{x-1}+\sqrt{x+2})\]
\[\Leftrightarrow \sqrt{{{x}^{2}}+x-2}-1=-\sqrt{x-1}+\sqrt{x+2}\]
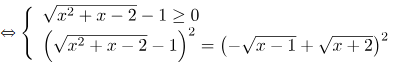
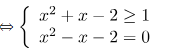
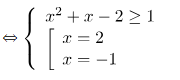
\[\Leftrightarrow x=2\] ( thỏa mãn đk)
4. Phương pháp 4: Đưa về phương trình tích
Bài toán: Giải phương trình: \[\sqrt{x+3}+2x\sqrt{x+1}=2x+\sqrt{{{x}^{2}}+4x+3}\]
Đk: \[x\ge -1\]
\[\Leftrightarrow \sqrt{x+3}+2x\sqrt{x+1}=2x+\sqrt{{{x}^{2}}+4x+3}\]
\[\Leftrightarrow \sqrt{x+3}-\sqrt{(x+1)(x+3)}-(2x-2x\sqrt{x+1})=0\]
\[\Leftrightarrow \sqrt{x+3}(1-\sqrt{x+1})-2x\left( 1-\sqrt{x+1} \right)=0\]
\[\Leftrightarrow (1-\sqrt{x+1})(\sqrt{x+3}-2x)\]
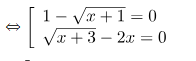
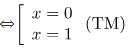
5. Phương pháp 5: Đặt ẩn phụ đưa về hệ phương trình
Bài toán: Giải phương trình:\[\sqrt{2x+8}-\sqrt[3]{2x-9}=5\]
Đk: \[x\ge -4\]
\[a=\sqrt{2x+8}\ge 0;b=\sqrt[3]{2x-9}\ge \sqrt[3]{-17}\]
Ta có: 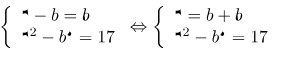
\[\Rightarrow {{(b+5)}^{2}}-{{b}^{3}}=17\] \[\Leftrightarrow \] 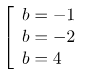
Với
\[b=-1\Rightarrow \sqrt[3]{2x-9}=-1\Leftrightarrow x=4\]
\[b=-2\Rightarrow \sqrt[3]{2x-9}=-2\Leftrightarrow x=\frac{1}{2}\]
\[b=4\Rightarrow \sqrt[3]{2x-9}=4\Leftrightarrow x=\frac{73}{2}\]
Vậy nghiệm của PT đã cho là x = 4, \[x=\frac{1}{2}\], \[x=\frac{73}{2}\]
6. Phương pháp 6: Phương pháp đánh giá
Bài toán: Giải phương trình: \[\sqrt{1-2012x}+\sqrt{1+2012x}=\sqrt{x+1}+\frac{1}{\sqrt{x+1}}\]
Đk: \[-\frac{1}{2012}\le x\le \frac{1}{2012}\]
Ta có: \[\sqrt{x+1}+\frac{1}{\sqrt{x+1}}\ge 2\]. Dấu = xảy ra khi x = 0
Ta có : \[{{\left( \sqrt{1-2012x}+\sqrt{1+2012x} \right)}^{2}}\le 2\left( 1-2012x+1+2012x \right)\]
\[\Rightarrow \sqrt{1-2012x}+\sqrt{1+2012x}\le 2\]
Dấu = xảy ra khi x = 0. Vậy x = 0 là nghiệm của PT đã cho







