Câu 1: Gọi \[{{t}_{1}}\] là thời gian ngắn nhất vật đi từ vị trí có li độ \[\frac{-A}{2}\] đến vị trí lực hồi phục đổi chiều; \[{{t}_{2}}\] là thời gian ngắn nhất vật đi từ vị trí có li độ \[\frac{A}{2}\] đến vị trí có li độ \[\frac{A\sqrt{3}}{2}\]; \[{{t}_{3}}\] là thời gian ngắn nhất vật đi từ vị trí có li độ \[\frac{A\sqrt{3}}{2}\] đến - A. Hệ thức đúng là
A.\[{{t}_{1}}:{{t}_{2}}:{{t}_{3}}=1:1:5\]
B.\[{{t}_{1}}:{{t}_{2}}:{{t}_{3}}=5:1:1\]
C.\[{{t}_{1}}:{{t}_{2}}:{{t}_{3}}=5:5:1\]
D.\[{{t}_{1}}:{{t}_{2}}:{{t}_{3}}=1:5:1\]
Hướng dẫn
\[{{t}_{1}}\] là thời gian ngắn nhất vật đi từ vị trí có li độ \[\frac{-A}{2}\] đến vị trí lực hồi phục đổi chiều: \[{{t}_{1}}=\frac{T}{12}\]
\[{{t}_{2}}\] là thời gian ngắn nhất vật đi từ vị trí có li độ \[\frac{A}{2}\] đến vị trí có li độ \[\frac{A\sqrt{3}}{2}\]: \[{{t}_{2}}=\frac{T}{12}\]
\[{{t}_{3}}\] là thời gian ngắn nhất vật đi từ vị trí có li độ \[\frac{A\sqrt{3}}{2}\] đến – A: \[{{t}_{3}}=\frac{5T}{12}\]
Vậy tỉ lệ là \[{{t}_{1}}:{{t}_{2}}:{{t}_{3}}=1:1:5\]
Chọn đáp án A
Câu 2: Vật dao động điều hòa gọi \[{{t}_{1}}\] là thời gian ngắn nhất vật đi li độ x=\[\frac{A}{2}\] đến li độ x=\[\frac{A\sqrt{3}}{2}\] và \[{{t}_{2}}\] là thời gian vật đi từ VTCB đến li độ \[x=-\frac{A\sqrt{2}}{2}\]. Mối quan hệ giữa \[{{t}_{1}}\] và \[{{t}_{2}}\] là
A. \[{{t}_{1}}\]=0,5\[{{t}_{2}}\] B. \[{{t}_{2}}\]=3\[{{t}_{1}}\] C. \[{{t}_{2}}\]=2\[{{t}_{1}}\] D. 2\[{{t}_{2}}\]=3\[{{t}_{1}}\]
Hướng dẫn
vật đi từ li độ x=\[\frac{A}{2}\] đến li độ x=\[\frac{A\sqrt{3}}{2}\] hết khoảng thời gian ngắn nhất là: \[{{t}_{1}}=\frac{T}{12}\]
vật đi từ VTCB đến li độ \[x=-\frac{A\sqrt{2}}{2}\] hết khoảng thời gian ngắn nhất là : \[{{t}_{2}}=\frac{T}{8}\]
Vậy 2\[{{t}_{2}}\]=3\[{{t}_{1}}\]
Chọn đáp án D
Câu 3: Một vật dao động điều hòa theo phương ngang từ B đến C với chu kỳ là T, vị trí cân bằng là trung điểm O của BC. Gọi M và N lần lượt là trung điểm của OB và OC, khoảng thời gian ngắn nhất để vật đi từ M đến N là
A. \[\Delta \]t = T/4. B. \[\Delta \]t = T/2. C. \[\Delta \]t = T/3. D. \[\Delta \]t = T/6.
Hướng dẫn
Khoảng thời gian vật đi từ M đến N là \[\frac{T}{6}\]
Chọn đáp án D
Câu 4: Một vật dao động điều hòa dọc theo một đường thẳng. Một điểm M nằm cố định trên đường thẳng đó, phía ngoài khoảng chuyển động của vật. Tại thời điểm t thì vật xa M nhất, sau đó một khoảng thời gian ngắn nhất là \[\vartriangle \]t vật gần M nhất. Vật cách vị trí cân bằng một khoảng
A.\[t+\frac{\Delta t}{4}\] B.\[t+\frac{\Delta t}{3}\] C.\[t+\frac{\Delta t}{2}\] D.\[t+\frac{\Delta t}{6}\]
Hướng dẫn
Giả sử vật M ở gần biên âm. Xa điểm M nhất nằm ở biên dương nên \[\Delta t=\frac{T}{2}\Rightarrow T=2\Delta t\]
Vật cách vị trí cân bằng một khoảng \[\frac{A}{\sqrt{2}}\]vào thời điểm gần nhất là \[{{t}_{\min }}=t+\frac{T}{8}=\]\[t+\frac{\Delta t}{4}\]
Chọn đáp án A
Câu 5: Một vật dao động điều hòa trên trục Ox với biên độ 25 cm và tần số f. Thời gian ngắn nhất để vận tốc của vật có giá trị từ - 7π cm/s đến 24π cm/s là \[\frac{1}{4f}\] . Gia tốc cực đại của vật trong quá trình dao động là
A.1,2\[m/{{s}^{2}}\] B.2,5\[m/{{s}^{2}}\] C.1,4\[m/{{s}^{2}}\] D.1,5\[m/{{s}^{2}}\]
Hướng dẫn
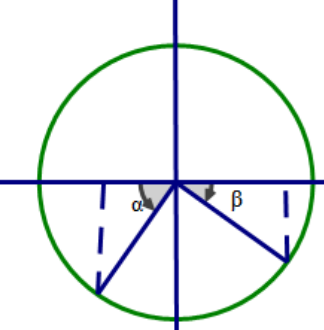
Thời gian ngắn nhất để vận tốc của vật có giá trị từ - 7π cm/s đến 24π cm/s là \[\frac{1}{4f}\to t=\frac{T}{4}\to \vartriangle \varphi =\frac{\pi }{2}\]
Sử dụng vòng tròn lượng giác ta có
.png)
Gia tốc cực đại của vật trong quá trình dao động là: \[a={{\omega }^{2}}A=2500cm/{{s}^{2}}\]
Chọn đáp án B
Câu 6: Khi điện tích trên tụ tăng từ 0 lên 0,5 μC thì đồng thời cường độ dòng điện trong mạch dao động LC lí tưởng giảm từ 3π (mA) xuống \[\frac{3\sqrt{3}\pi }{2}\] (mA). Khoảng thời gian xảy ra sự biến thiên này là
A.\[\frac{1}{18}\mu s\] B.\[\frac{1}{6}\mu s\] C.\[\frac{1}{6}ms\] D.\[\frac{1}{18}ms\]
Hướng dẫn
Khi điện tích bằng 0 thì \[i=3\pi \left( mA \right)={{I}_{0}}\]
Khi điện tích q = 0,5 μC thì \[i=\frac{3\sqrt{3}\pi }{2}\to {{\left( \frac{q}{{{q}_{o}}} \right)}^{2}}+{{\left( \frac{i}{{{I}_{o}}} \right)}^{2}}=1\to {{q}_{o}}=1\mu C\]
→ Thời gian để q tăng từ 0 lên \[q=0,5\mu C=\frac{{{q}_{o}}}{2}\] là \[\frac{T}{12}\] \[=\frac{2\pi {{q}_{o}}}{{{I}_{o}}}=\frac{1}{18}ms\]
Chọn đáp án D
Câu 7: Một mạch dao động LC lí tưởng đang có dao động điện từ tự do. Tại thời điểm t = 0, điện áp giữa hai bản tụ có độ lớn bằng nửa giá trị cực đại và có độ lớn đang giảm. Sau khoảng thời gian ngắn nhất \[\Delta t={{2.10}^{-6}}s\] thì điện áp giữa hai bản tụ có độ lớn đạt giá trị cực đại. Tần số dao động của mạch là
A.\[{{3.10}^{6}}Hz\] B.\[{{6.10}^{6}}Hz\] C.\[\frac{{{10}^{6}}}{6}Hz\] D.\[\frac{{{10}^{6}}}{3}Hz\]
Hướng dẫn
Khoảng thời gian cần tìm là t=T/3 suy ra \[T={{3.2.10}^{-6}}\Rightarrow \] tần số dao động của mạch là \[\frac{{{10}^{6}}}{6}Hz\]
Chọn đáp án C
Câu 8: Một mạch dao động điện từ LC lí tưởng đang có dao động điện từ tự do. Biết điện tích cực đại trên một bản tụ điện là \[{{q}_{o}}=1\mu C\] và cường độ dòng điện cực đại trong mạch là \[{{I}_{o}}=3\pi mA\] . Tính từ thời điểm điện tích trên tụ là \[{{q}_{o}}\] , khoảng thời gian ngắn nhất để dòng điện trong mạch có độ lớn bằng \[{{I}_{o}}\] là
A.\[\frac{10}{3}ms\] B.\[\frac{1}{6}\mu s\] C.\[\frac{1}{2}\mu s\] D.\[\frac{1}{6}ms\]
Hướng dẫn
Chu kì dao động của mạch là \[T=2\pi \sqrt{LC}=\frac{2\pi {{q}_{o}}}{{{I}_{o}}}\approx 6,{{67.10}^{-4}}s\]
Khoảng thời gian ngắn nhất từ \[{{q}_{o}}\] đến \[{{I}_{o}}\] là \[\frac{T}{4}=\frac{1}{6}ms\]
Chọn đáp án D
Câu 9: Trong mạch dao động LC lí tưởng đang có dao động điện từ tự do. Thời gian ngắn nhất giữa hai lần liên tiếp năng lượng từ trường bằng ba lần năng lượng điện trường là \[{{10}^{-4}}s\].Thời gian giữa ba lần liên tiếp dòng điện trên mạch có giá trị lớn nhất là
A.\[{{3.10}^{-4}}s\] B.\[{{9.10}^{-4}}s\] C.\[{{6.10}^{-4}}s\] D.\[{{2.10}^{-4}}s\]
Hướng dẫn
Có \[{{\text{W}}_{tt}}=3{{W}_{dt}}\to {{\text{W}}_{dt}}=\frac{1}{4}\text{W}\to \frac{1}{2}C{{u}^{2}}=\frac{1}{4}.\frac{1}{2}CU_{o}^{2}\to u=\frac{1}{2}{{U}_{o}}\]
Thời gian ngắn nhất giữa 2 lần liên tiếp \[u=\frac{1}{2}{{U}_{o}}\] là \[\frac{T}{6}={{10}^{-4}}s\to T={{6.10}^{-4}}s\]
Chọn đáp án C
Thời gian giữa 3 lần liên tiếp dòng điện trên mạch có giá trị lớn nhất là \[T={{6.10}^{-4}}s\]
Câu 10: Đặt điện áp u = 400cos100\[\pi \]t (u tính bằng V, t tính bằng s) vào hai đầu đoạn mạch AB gồm điện trở thuần 50 \[\Omega \] mắc nối tiếp với đoạn mạch X. Cường độ dòng điện hiệu dụng qua đoạn mạch là 2 A. Biết ở thời điểm t, điện áp tức thời giữa hai đầu AB có giá trị 400 V, ở thời điểm \[t+\frac{1}{400}\] (s), cường độ dòng điện tức thời qua đoạn mạch bằng không và đang giảm. Công suất tiêu thụ điện của đoạn mạch X là
A. 400 W. B. 200 W. C. 160 W. D. 100 W.
Hướng dẫn
Ta có:\[U=200\sqrt{2};I=2A\to Z=100\sqrt{2}\Omega \]
Ở thời điểm t:\[u=100V\to 100\pi t=k2\pi (1)\]
Giả sử: \[i=2\sqrt{2}\cos \left( 100\pi t+{{\varphi }_{i}} \right)(A)\]
Ở thời điểm \[t+\frac{1}{400}\] (s), i=0A và đang giảm nên \[100\pi t+{{\varphi }_{i}}=100\pi t+\frac{\pi }{4}+{{\varphi }_{i}}=\frac{\pi }{2}+k2\pi \Rightarrow \frac{\pi }{4}+{{\varphi }_{i}}=\frac{\pi }{2}\to {{\varphi }_{i}}=\frac{\pi }{4}\]
Góc lệch pha giữa u và i là \[\varphi ={{\varphi }_{u}}-{{\varphi }_{i}}=-\frac{\pi }{4}\]
Công suất tiêu thụ điện của đoạn mạch X là \[{{P}_{X}}=P-{{P}_{R}}=UI{{\cos }_{\varphi }}-{{I}^{2}}R=200W\]
Chọn đáp án B
Câu 11: Một mạch điện xoay chiều gồm AM nối tiếp MB. Biết AM gồm điện trở thuần \[{{R}_{1}}\] , tụ điện \[{{C}_{1}}\] , cuộn dây thuần cảm \[{{L}_{1}}\]mắc nối tiếp. Đoạn MB có hộp X, biết trong hộp X cũng có các phần tử là điện trở thuần, cuộn cảm, tụ điện mắc nối tiếp nhau. Đặt điện áp xoay chiều vào hai đầu mạch AB có tần số 50 Hz và giá trị hiệu dụng là 200 V thì thấy dòng điện trong mạch có giá trị hiệu dụng \[\sqrt{3}\]A. Biết \[{{R}_{1}}=50\Omega \] và nếu ở thời điểm t (s), \[{{u}_{AB}}=200V\] và đang tăng thì ở thời điểm \[t+\frac{1}{300}\]s dòng điện \[i=\sqrt{3}A\]và đang giảm. Công suất của đoạn mạch MB là
A. 300 W B. 120 W C. 200 W D. 150 W
Hướng dẫn

Ta có:
.png)
từ t tới thời điểm \[t+\frac{1}{300}\]s thì i đã dịch chuyển 1 góc là \[\vartriangle \varphi =\frac{\pi }{3}\to \vartriangle {{\varphi }_{ui}}=-\frac{\pi }{6}\]
Công suất toàn mạch là \[P=UI\cos {{\varphi }_{ui}}=300W\]
Công suất qua điện trở thuần đoạn AM là \[{{P}_{R}}={{I}^{2}}R=150W\]
Công suất mạch qua đoạn MB là \[{{P}_{MB}}=P-{{P}_{R}}=150W\]
Chọn đáp án D
Câu 12: Một mạch điện xoay chiều gồm AM nối tiếp MB. Biết AM gồm điện trở thuần \[{{R}_{1}}\] , tụ điện \[{{C}_{1}}\] , cuộn dây thuần cảm \[{{L}_{1}}\]mắc nối tiếp. Đoạn MB có hộp X, biết trong hộp X cũng có các phần tử là điện trở thuần, cuộn cảm, tụ điện mắc nối tiếp nhau. Đặt điện áp xoay chiều vào hai đầu mạch AB có tần số 50 Hz và giá trị hiệu dụng là 200 V thì thấy dòng điện trong mạch có giá trị hiệu dụng 2A. Biết \[{{R}_{1}}=25\Omega \] và nếu ở thời điểm t (s), \[{{u}_{AB}}=200V\] và đang tăng thì ở thời điểm \[t+\frac{1}{600}\] s dòng điện i = 2 A và đang giảm. Công suất của đoạn mạch MB là
A. 100 W B. 120 W C. 200 W D. 400 W
Hướng dẫn
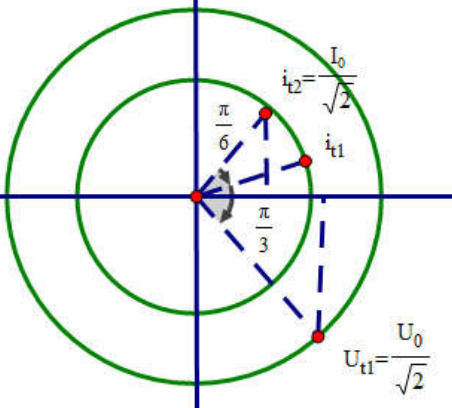
Ta có:
.png)
từ t tới thời điểm \[t+\frac{1}{600}\]s thì i đã dịch chuyển 1 góc là \[\vartriangle \varphi =\frac{\pi }{6}\to \vartriangle {{\varphi }_{ui}}=-\frac{\pi }{3}\]
Công suất toàn mạch là \[P=UI\cos {{\varphi }_{ui}}=200W\]
Công suất qua điện trở thuần đoạn AM là \[{{P}_{R}}={{I}^{2}}R=100W\]
Công suất mạch qua đoạn MB là \[{{P}_{MB}}=P-{{P}_{R}}=100W\]
Chọn đáp án A
Câu 13: Một vật dao động điều hòa với phương trình \[x=4\sqrt{2}\cos \left( \omega t+\frac{\pi }{6} \right)cm\] . Trong 1 chu kì, khoảng thời gian mà vật cách vị trí cân bằng không quá \[2\sqrt{2}\] cm là 1/6 (s). Vật qua li độ \[x=-2\sqrt{6}\] m theo chiều âm lần 2017 vào thời điểm nào?
A. 2017/48 (s) B. 3024/3 (s) C. 6049/6 (s) D. 1003/20 (s)
Hướng dẫn
Thời gian vật cách vị trí cân bằng không quá \[2\sqrt{2}\] là 1/6 (s) \[\Rightarrow \frac{1}{6}=\frac{T}{3}\Rightarrow T=\frac{1}{2}s\Rightarrow \omega =4\pi rad/s\]
Trong 1 chu kì vật qua vị trí có li độ \[x=-2\sqrt{6}\]theo chiều âm 1 lần.
Vẽ đường tròn ta thấy vật đi qua lần đầu khi \[\varphi =\frac{2\pi }{3}\Rightarrow t=\frac{\varphi }{\omega }=\frac{T}{3}(s)\]
Vật đi 2016 lần đầu trong 2016T.
Vậy vật qua vị trí có li độ \[x=-2\sqrt{6}\] cm theo chiều âm lần thứ 2017 tại thời điểm \[t=2016T+\frac{T}{3}=\frac{6049}{6}s\]
Chọn đáp án C
Câu 14: Vật dao động điều hòa với biên độ A = 10 cm, gia tốc của vật bằng 0 tại hai thời điểm liên tiếp là \[{{t}_{1}}=\frac{41}{16}s\] và \[{{t}_{2}}=\frac{45}{16}s\] . Biết tại thời điểm t = 0 vật đang chuyển động về biên dương. Thời điểm vật qua vị trí có li độ x = 5 cm lần thứ 2017 là:
A. 584,5 s B. 503,8 s C. 503,6 s D. 504,1 s
Hướng dẫn
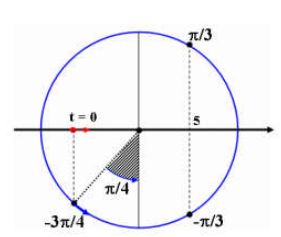
Ta thấy \[\vartriangle t={{t}_{2}}-{{t}_{1}}=\frac{T}{2}\Rightarrow T=0,5s\]
Tại thời điểm \[{{t}_{1}}=\frac{41}{16}s\]\[=5T+\frac{T}{8}\]
Mà tại t = 0 vật chuyển động về biên dương.
\[\Rightarrow \] Tại t = 0 vật có li độ \[\frac{-A}{\sqrt{2}}\] và đang chuyển động theo chiều dương.
Phương trình dao động \[x=10\cos \left( 4\pi t-\frac{3\pi }{4} \right)(cm)\]
Trong 1 chu kì vật đi qua vị trí có li độ x=5cm hai lần
Mà 2017= 2016 +1 nên \[{{t}_{2017}}=\frac{2016}{2}T+{{t}_{1}}=1008T+{{t}_{1}}\] ; ở đây \[{{t}_{1}}\] là thời
điểm lần thứ 1 vật qua tọa độ x =5 kể từ khi dao động.
Vẽ trục ta dễ dàng có được \[{{t}_{1}}=\frac{T}{8}+\frac{T}{6}=\frac{7T}{24}\Rightarrow {{t}_{2017}}=1008T+\frac{7T}{24}=504,1s\]
Chọn đáp án D







