phạm quang đông

Trong không gian với hệ trục tọa độ Oxyz, cho mặt phẳng $\left( P \right):x + 2y + z - 4 = 0$ và đường thẳng $d:\frac{{x + 1}}{2} = \frac{y}{1} = \frac{{z + 2}}{3}.$ Viết phương trình đường thẳng $\Delta $ nằm trong mặt phẳng $\left( P \right),$ đồng thời cắt và vuông góc với đường thẳng d.

Trong không gian với hệ tọa độ Oxyz cho đường thăng \[\Delta :\frac{x}{1}=\frac{y-1}{1}=\frac{z-2}{-1}\] và mặt

phẳng \[\left( P \right):x+2y+2z-4=0.\] Phương trình đường thăng d nằm trong \[\left( P \right)\] sao cho d cắt và vuông góc với đường thẳng \[\Delta \] là:

Trong không gian với hệ trục tọa độ Oxyz cho hai điểm \[A\left( 1;0;-3 \right),\text{ }B\left( -3;-2;-5 \right).\] Biết rằng tập hợp các điểm M trong không gian thỏa mãn đẳng thức $A{{M}^{2}}+B{{M}^{2}}=30$ là một mặt cầu$\left( S \right)$. Tọa độ tâm I và bán kính R của mặt cầu $\left( S \right)$ là:

Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P) đi qua điểm \[M\left( 1;2;3 \right)\] và cắt các trục Ox, Oy, Oz lần lượt tại các điểm A, B, C (khác O). Viết phương trình mặt phẳng (P) sao cho M là trực tâm của tam giác ABC.

Trong không gian với hệ tọa độ $Oxyz$, cho đường thẳng ∆ đi qua điểm $M\left( 0;1;1 \right)$, vuông góc với đường thẳng 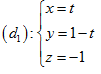và cắt đường thẳng $\left( {{d}_{2}} \right):\frac{x}{2}=\frac{y-1}{1}=\frac{z}{1}$. Phương trình của ∆ là:

(I)        (II)        (III)        (IV)

Trong không gian với hệ tọa độ Oxyz, cho mặt cầu $\left( S \right):{{\left( x-1 \right)}^{2}}+{{\left( y-2 \right)}^{2}}+{{\left( z-3 \right)}^{2}}=16$ và các điểm \[A\text{ }\left( 1;0;2 \right),\text{ }B\text{ }\left( -1;2;2 \right).\] Gọi (P) là mặt phẳng đi qua hai điểm A, B sao cho thiết diện của mặt phẳng (P) với mặt cầu (S) có diện tích nhỏ nhất. Khi viết phương trình (P) dưới dạng \[ax+by+cx+3=0.\] Tính tổng \[T=a+b+c.\]

Trong không gian Oxyz, cho mặt phẳng

đường thẳng

$d:\frac{x+1}{1}=\frac{y+2}{2}=\frac{z+3}{2}$ và điểm $A\left( \frac{1}{2};1;1 \right)$. Gọi $\Delta $ là đường thẳng nằm trong mặt phẳng

, song song với d đồng thời cách d một khoảng bằng 3. Đường thẳng $\Delta $ cắt mặt phẳng (Oxy) tại điểm B. Độ dài đoạn thẳng AB bằng:

Trong không gian với hệ trục tọa độ Oxyz, cho ba điểm $A\left( {1;2; - 1} \right),B\left( {2;1;1} \right),C\left( {0;1;2} \right).$ Gọi điểm $H\left( {x;y;z} \right)$ là trực tâm tam giác ABC. Giá trị của $S = a + y + z$ là

Trong không gian \[Oxyz,\] cho\[A\left( 1;-1;2 \right),\text{ }B\left( -2;0;3 \right),\text{ }C\left( 0;1;-2 \right).\,\,M\left( a;b;c \right)\] là điểm thuộc mặt phẳng $\left( Oxy \right)$ sao cho biểu thức \[S=\overrightarrow{MA}.\overrightarrow{MB}+2\overrightarrow{MB}.\overrightarrow{MC}+3\overrightarrow{MC}.\overrightarrow{MA}\] đạt giá trị nhỏ nhất. Khi đó \[T=12a+12b+c\] có giá trị là

Trong không gian với hệ trục tọa độ $Oxyz$, cho điểm $A\left( 3;-2;1 \right)$ và mặt phẳng $\left( P \right):x+y+2z-5=0$. Đường thẳng nào sau đây đi qua $A$ và song song với mặt phẳng $\left( P \right)$?