thi thử TNTHPT

Hình dưới đây là đồ thị của hàm số \[y=f'\left( x \right)\]. 

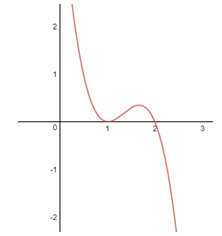
Hỏi hàm số \[y=f\left( x \right)\] có bao nhiêu điểm cực trị ? 

Một phân tử polietilen có khối lượng phân tử bằng 56000u. Hệ số polime hóa của phân tử polietylen này là:

Tìm tập các giá trị của tham số m để đồ thị hàm số $y=\frac{{{x}^{2}}+{{m}^{2}}x-m-1}{x+2}$ có tiệm cận đứng.

Có bao nhiêu giá trị nguyên của tham số m để hàm số $y=\frac{mx+4}{x+m}$ giảm trên khoảng $\left( -\infty ;1 \right)?$ 

Số giá trị $m$ nguyên trên $\left[ -2;2018 \right]$  để hàm số $y={{e}^{{{x}^{3}}-{{x}^{2}}+mx}}$ đồng  biến trên $\left[ 1,2 \right]$.

Cho hàm số $y=\frac{2x-3}{x-2}\left( C \right).$ Gọi d là tiếp tuyến bất kì của (C) d, cắt hai đường tiệm cận của đồ thị (C) lần lượt tại A, B . Khi đó khoảng cách giữa A và B ngắn nhất bằng

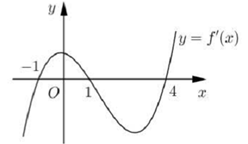
Cho hàm số $y=f\left( x \right)$. Hàm số $y={f}'\left( x \right)$ có đồ thị như hình bên. Hàm số $y=f\left( {{x}^{2}}+1 \right)$ có bao nhiêu điểm cực trị?

Ông A vay ngắn hạn ngân hàng 100 triệu đồng với lãi suất 12%/năm, theo thỏa thuận cứ mỗi tháng ông A phải trả cho ngân hàng a triệu đồng. Hỏi a bằng bao nhiêu để ông A trả hết nợ ngân hàng sau đúng 3 tháng. Biết rằng lãi suất ngân hàng không thay đổi trong thời gian ông A hoàn nợ, a tính theo đơn vị triệu đồng.

Cho a là một số dương, biểu thức ${{a}^{\frac{2}{3}}}\sqrt[{}]{a}.$ Viết dưới dạng luỹ thừa với số mũ hữu tỉ.

Tìm n biết $\frac{1}{{{\log }_{2}}x}+\frac{1}{{{\log }_{{{2}^{2}}}}x}+\frac{1}{{{\log }_{{{2}^{3}}}}x}+...+\frac{1}{{{\log }_{{{2}^{n}}}}x}=\frac{465}{{{\log }_{2}}x}$ luôn đúng với mọi $x>0,x\ne 1.$

Cho \[{{\log }_{b}}\left( a+1 \right)>0\], khi đó khẳng định nào sau đây là đúng ?

 Tìm tất cả các giá trị của tham số $m$ để hàm số $y=\ln \left( 16{{x}^{2}}+1 \right)-\left( m+1 \right)x+m+2$ nghịch biến trên khoảng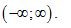  

Diện tích S của hình phẳng giới hạn bởi đồ thị hàm số \[y=f\left( x \right),\]liên tục trên \[\left[ a;b \right]\] trục hoành và hai đường thẳng \[x=a,x=b\left( a

Diện tích S của hình phẳng giới hạn bởi đồ thị các hàm số $y=x$và $y={{e}^{x}}$, trục tung và đường thẳng $x=1$ được tính theo công thứ:

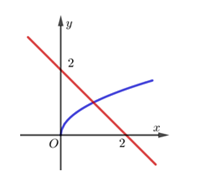
Cho hình phẳng giới hạn bởi đồ thị hàm số $y=\sqrt{x}$, đường thẳng $y=2-x$ và trục hoành. Thể tích của khối tròn xoay sinh bởi hình phẳng trên khi quay quanh trục Ox bằng:

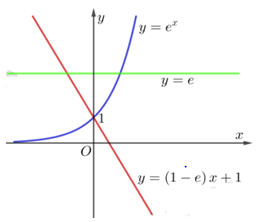
Cho $\left( H \right)$ là hình phẳng giới hạn bởi các đồ thị hàm số $y=e,y={{e}^{x}}$ và $y=\left( 1-e \right)x+1$ (tham khảo hình vẽ). Diện tích của $\left( H \right)$là

Cho số phức $2-3i.$ Môđun của số phức$\text{w}=\left( 1+i \right)z$ bằng:

Số phức $z=a+bi\left( a,b\in \mathbb{R} \right)$ thỏa mãn $\left| z-2 \right|=\left| z \right|$ và $\left( z+1 \right)\left( \bar{z}-i \right)$ là số thực. Giá trị của biểu thức $S=a+2b$ bằng bao nhiêu?

Cho số phức thỏa mãn $\left| z-2i \right|\le \left| z-4i \right|$ và $\left| z-3-3i \right|=1.$ Giá trị lớn nhất của $P=\left| z-2 \right|$ là:

Cho số phức z thỏa mãn  Biết biểu thức 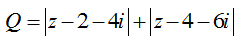 đạt giá trị nhỏ nhất tại z = a + bi (a, b ∈ R). Tính P = a − 4b

Xét các số phức \[z=a+bi,\left( a,b\in \mathbb{R} \right)\]  thỏa mãn $\left| z-1+2i \right|=\sqrt{5}.$

Tìm P= 16a+8b  biết $\left| z+1+i \right|+\left| z-1+4i \right|$ đạt giá trị lớn nhất.

Một cái bồn gồm hai nửa hình cầu đường kính 18dm và một hình trụ có chiều cao

36dm (như hình vẽ). Tính thể tích V của cái bồn đó.

Gọi ${{V}_{1}}$ là thể tích của khối lập phương $ABCD.A'B'C'D',{{V}_{2}}$  là thể tích khối tứ diện

$A'ABD.$ Hệ thức nào sau đây là đúng ?

Tính thể tích khối bát diện đều cạnh a 

Xét khối tứ diện \[ABCD,AB=x,\] các cạnh còn lại bằng $2\sqrt{3}.$ Tìm x để thể tích khối tứ diện ABCD lớn nhất.

Cho hình vuông \[{{A}_{1}}{{B}_{1}}{{C}_{1}}{{D}_{1}}\] có cạnh bằng 1. Gọi \[{{A}_{k+1}},{{B}_{k+1}},{{C}_{k+1}},{{D}_{k+1}}\] thứ tự là trung điểm các cạnh \[{{A}_{k}}{{B}_{k}},{{B}_{k}}{{C}_{k}},{{C}_{k}}{{D}_{k}},{{D}_{k}}{{A}_{k}}\] (với \[k=1,2,...\]). Chu vi của hình vuông \[{{A}_{2018}}{{B}_{2018}}{{C}_{2018}}{{D}_{2018}}\] là

Trong không gian với hệ trục tọa độ Oxyz, cho hai điểm $M\left( 0;3;-2 \right)$ và $N\left( 2;-1;0 \right)$. Tọa độ của véc tơ $\overrightarrow{MN}$ là:

Trong không gian với hệ tọa độ \[Oxyz\], cho đường thẳng \[\Delta \] đi qua điểm \[M\left( 2;0;-1 \right)\] và có vectơ chỉ phương \[\overrightarrow{a}=\left( 4;-6;2 \right)\]. Phương trình tham số của \[\Delta \] là

Trong không gian Oxyz, cho hai mặt phẳng

và

. Tìm m để hai mặt phẳng

và

song song với nhau.

Trong không gian với hệ trục tọa độ Oxyz, cho mặt phẳng $\left( P \right):x + 2y + z - 4 = 0$ và đường thẳng $d:\frac{{x + 1}}{2} = \frac{y}{1} = \frac{{z + 2}}{3}.$ Viết phương trình đường thẳng $\Delta $ nằm trong mặt phẳng $\left( P \right),$ đồng thời cắt và vuông góc với đường thẳng d.

Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S) có phương trình

${{\left( x-1 \right)}^{2}}+{{\left( y-2 \right)}^{2}}+{{\left( z+1 \right)}^{2}}=1$, phương trình mặt phẳng (Q) chứa trục hoành và tiếp xúc với mặt cầu (S) là:

 Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng $\left( P \right):x+y-z-1=0$ và điểm $A\left( 1;0;0 \right)\in \left( P \right).$ Đường thẳng $\Delta $ đi qua A nằm trong mặt phẳng $\left( P \right)$ và tạo với trục Oz một góc nhỏ nhất. Gọi $M\left( {{x}_{0}};{{y}_{0}};{{z}_{0}} \right)$ là giao điểm của đường thẳng $\Delta $với mặt phẳng $\left( Q \right):2x+y-2z+1=0$. Tổng $S={{x}_{0}}+{{y}_{0}}+{{z}_{0}}$ bằng:

Trong không gian với tọa độ Oxyz, cho điểm $A\left( {1;2; - 3} \right)$ và mặt phẳng $\left( P \right):2x + 2y - z + 9 = 0.$ Đường thẳng d đi qua A và có vecto chỉ phương $\overrightarrow u \left( {3;4; - 4} \right)$ cắt $\left( P \right)$ tại điểm B. Điểm M thay đổi trong $\left( P \right)$ sao cho M luôn nhìn đoạn AB dưới góc $90^\circ .$ Khi độ dài MB lớn nhất, đường thẳng MB đi qua điểm nào trong các điểm sau

Độ giảm huyết áp của một bệnh nhân được cho bởi công thức $G\left( x \right)=0,025{{x}^{2}}\left( 30-x \right)$. Trong đó x là liều lượng thuốc được tiêm cho bệnh nhân (đơn vị miligam). Tính liều lượng thuốc cần tiêm cho bệnh nhân để huyết áp giảm nhiều nhất.

Tìm tất cả các số tự nhiên k sao cho $C_{14}^{k},C_{14}^{k+1},C_{14}^{k+2}$ theo thứ tự lập thành một cấp số cộng.

Tung 1 con súc sắc cân đối và đồng chất hai lần liên tiếp. Xác suất để kết quả của hai lần tung là hai số tự nhiên liên tiếp bằng: