LỰC HƯỚNG TÂM
Câu 1: Một vệ tinh có khối lượng m = 60 kg đang bay trên quỹ đạo tròn quanh Trái Đất ở độ cao bằng bán kính Trái Đất. Biết Trái Đất có bán kính R = 6400 km. Lấy g = 9,8 m/s2. Tính tốc độ dài của vệ tinh.
A. 6,4 km/s. B. 11,2 km/s. C. 4,9 km/s. D. 5,6 km/s.
Hướng dẫn
Lực hấp dẫn đóng vai trò là lực hướng tâm \[{{F}_{ht}}={{F}_{hd}}\]
Có: \[g=\frac{GM}{{{r}^{2}}}\] (với \[r=R+R=2\text{R}\])
\[\frac{m{{v}^{2}}}{r}=\frac{GMm}{{{r}^{2}}}\Leftrightarrow \frac{{{v}^{2}}}{r}=g\]
\[\Rightarrow {{v}^{2}}=gr={{9,8.10}^{-3}}.2.6400=125,44\]
\[\Rightarrow v=11,2km/s\]
Câu 2: Chu kì chuyển động của Mặt Trăng quanh Trái Đất là 27,32 ngày và khoảng cách từ Trái Đất tới Mặt Trăng là 3,84.108 m. Hãy tính khối lượng của Trái Đất. Giả thiết quỹ đạo chuyển động của Mặt Trăng là tròn.
A. 6,00.1024 kg. B. 6,45.1027 kg. C. 6,00.1027 kg. D. 6,45.1024 kg.
Hướng dẫn
Ta có T = 27,32 ngày = 2360448s \[=\frac{2\pi }{\omega }\Rightarrow \omega =\frac{2\pi }{T}\]
Lực hấp dẫn đóng vai trò là lực hướng tâm.
\[m{{a}_{ht}}=\frac{GmM}{{{r}^{2}}}\Rightarrow {{\omega }^{2}}r=\frac{GM}{{{r}^{2}}}\]
\[\Rightarrow M=\frac{{{\omega }^{2}}{{r}^{3}}}{G}=\frac{4{{\pi }^{2}}{{r}^{3}}}{{{T}^{2}}G}={{6,00.10}^{24}}kg\]
Câu 3: Một vệ tinh khối lượng 100 kg, được phóng lên quỹ đạo quanh Trái Đất ở độ cao mà tại đó nó có trọng lượng 920 N. Chu kì của vệ tinh là 5,3.103 s. Tính khoảng cách từ bề mặt Trái Đất đến vệ tinh. Biết bán kính Trái Đất là 6400 km.
A. 135 km. B. 98 km. C. 185 km. D. 153 km.
Hướng dẫn
\[g=\frac{GM}{{{r}^{2}}}\]
Lực hấp dẫn đóng vai trò là lực hướng tâm.
\[\frac{m{{v}^{2}}}{r}=\frac{GMm}{{{r}^{2}}}=mg=P=920N\]
\[\Rightarrow {{F}_{ht}}=m{{a}_{ht}}=m{{\omega }^{2}}\left( R+h \right)=m\frac{4{{\pi }^{2}}}{{{T}^{2}}}\left( R+h \right)\]
\[\Rightarrow 100.\frac{4{{\pi }^{2}}}{{{\left( {{5,3.10}^{3}} \right)}^{2}}}\left( 6400+h \right)=920\]
\[\Rightarrow h=152699m=153km\]
Câu 4: Trong môn quay tạ, một vận động viên quay dây sao cho cả dây và chuyển động gần như tròn đều trong mặt phẳng nằm ngang. Muốn tạ chuyển động trên đường tròn bán kính 2 m với tốc độ dài 2 m/s thì người ấy phải giữ dây với một lực bằng 10 N. Hỏi khối lượng của tạ bằng bao nhiêu ?
A. 7,5 kg. B. 5 kg. C. 12 kg. D. 8,35 kg.
Hướng dẫn
Lực căng dây là lực hướng tâm.
\[{{F}_{ht}}=T\Rightarrow \frac{m{{v}^{2}}}{r}=10\Rightarrow m=\frac{10.2}{{{2}^{2}}}=5kg\]
Câu 5: Một người buộc một hòn đá vào đầu một sợi dây rồi quay dây trong mặt phẳng thẳng đứng. Hòn đá có khối lượng 0,4 kg chuyển động trên đường tròn bán kính 0,5 m với tốc độ không đổi 8 rad/s. Hỏi lực căng của dây khi hòn đá ở đỉnh của đường tròn ?
A. 8,88 N. B. 12,8 N. C. 3,92 N. D. 15,3 N.
Hướng dẫn
Khi hòn đá ở đỉnh của đường tròn thì trọng lực và lực căng dây đóng vai trò là lực hướng tâm.
\[{{F}_{ht}}=P+T\Rightarrow T={{F}_{ht}}-P\]
\[T=m{{\omega }^{2}}r-mg={{0,4.8}^{2}}.0,5-0,4.9.8=8,88N\]
Câu 6: Một quả cầu khối lượng 0,5 kg được buộc vào đầu của 1 sợi dây dài 0,5 m rồi quay dây sao cho quả cầu chuyển động tròn đều trong mặt phẳng nằm ngang và sợi dây làm thành một góc 300 so với phương thẳng đứng như hình vẽ. Lấy g = 9,8 m/s2. Xác định tốc độ dài của quả cầu.
A. 1,19 m/s. B. 1,93 m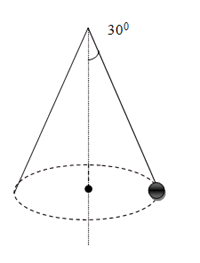 /s.
/s.
C. 0,85 m/s. D. 0,25 m/s.
Hướng dẫn
Tổng hợp lực của trọng lực và lực căng dây đóng vai trò là lực hướng tâm.
\[\Rightarrow \frac{{{F}_{ht}}}{P}=\tan {{30}^{0}}\Rightarrow {{F}_{ht}}=0,5.9,8.\tan {{30}^{0}}=2,83N\]
Quả cầu chuyển động theo quỹ đạo tròn với bán kính
\[r=l.\sin {{30}^{0}}=0,5.\sin {{30}^{0}}=0,25m\]
\[{{F}_{ht}}=\frac{m{{v}^{2}}}{r}\Rightarrow {{v}^{2}}=\frac{Fr}{m}=1,415\Rightarrow v=1,19m/s\]
Câu 7: Một ôtô khối lượng 2,5 tấn chuyển động qua một cầu vượt với tốc độ không đổi 54 km/h. Cầu vượt có dạng một cung tròn, bán kính 100 m. Tính áp lực của ôtô của ô tô lên cầu tại điểm cao nhất của quả cầu. Lấy g = 9,8 m/s2.
A. 15000 N. B. 19000 N. C. 22000 N. D. 17500 N.
Hướng dẫn
54 km/h = 15 m/s.
Khi ô tô đi đến điểm cao nhất của cầu thì một phần trọng lực đóng vai trò là lực hướng tâm.
\[{{F}_{ht}}=P-N\Rightarrow N=P-{{F}_{ht}}\]
\[\Rightarrow N=mg-\frac{m{{v}^{2}}}{R}={{2,5.10}^{3}}.9,8-\frac{{{2,5.10}^{3}}{{.15}^{2}}}{100}=18875\left( N \right)\]
Câu 8: Một bàn nằm ngang quay tròn đều với chu kì T = 2 s. Trên bàn đặt một vật cách trục quay R = 25 cm. Hệ số ma sát giữa vật và bàn tối thiểu bằng bao nhiêu để vật không trượt trên mặt bàn. Lấy g = 10 m/s2, π2 = 10.
A. 0,35. B. 0,05. C. 0,12. D. 0,25.
Hướng dẫn
Khi vật không trượt chịu tác dụng của 3 lực \[\overrightarrow{P},\overrightarrow{N},\overrightarrow{{{F}_{msn}}}\]
Trong đó \[\overrightarrow{P}+\overrightarrow{N}=\overrightarrow{0}\]
Lúc đó vật chuyển động tròn đều nên \[\overrightarrow{{{F}_{msn}}}\] đóng vai trò là lực hướng tâm.
Để vật không trượt trên bàn thì \[{{F}_{ht}}\le {{F}_{msn}}\Rightarrow m{{\omega }^{2}}R\le \mu mg\Rightarrow \mu \ge \frac{{{\omega }^{2}}R}{g}\]
\[\Rightarrow \mu \ge \frac{4{{\pi }^{2}}R}{{{T}^{2}}g}=0,25\Rightarrow {{\mu }_{\min }}=0,25\]
Câu 9: Một lò xo có độ cứng k, có chiều dài tự nhiên l0 một đầu giữ cố định ở A đầu kia gắn vào quả cầu khối lượng m có thể trượt không ma sát trên thanh (Δ) nằm ngang. Thanh (Δ) quay đều với vận tốc góc ω quanh trục (Δ) thẳng đứng. Tính độ dãn của lò xo khi l0 = 20 cm, ω = 20π rad/s, m = 10 g; k = 200 N/m.
A. 5 cm. B. 3,5 cm.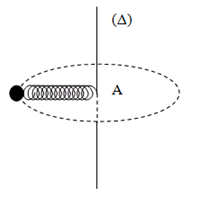
C. 6 cm. D. 8 cm.
Hướng dẫn
Lực đàn hồi của lò xo đóng vai trò là lực hướng tâm.
Khi trục \[\Delta \] quay thì lò xo giãn ra một đoạn \[\Delta l\].
\[{{F}_{ht}}={{F}_{dh}}\Leftrightarrow m{{\omega }^{2}}\left( {{l}_{0}}+\Delta l \right)=k\Delta l\Rightarrow \Delta l\left( k-m{{\omega }^{2}} \right)=m{{\omega }^{2}}{{l}_{0}}\]
\[\Rightarrow \Delta l=\frac{m{{\omega }^{2}}{{l}_{0}}}{k-m{{\omega }^{2}}}=\frac{0,01.{{\left( 20\pi \right)}^{2}}.0,2}{200-0,01.{{\left( 20\pi \right)}^{2}}}=0,05m=5cm\]
Câu 10: Vòng xiếc là một vành tròn bán kính R = 8 m, nằm trong mặt phẳng thẳng đứng. Một người đi xe đạp trên vòng xiếc này, khối lượng cả xe và người là 80 kg. Lấy g = 9,8 m/s2, tính lực ép của xe lên vòng xiếc tại điểm cao nhất với vận tốc tại điểm này là v = 10 m/s.
A. 164 N. B. 186 N. C. 254 N. D. 216 N.
Hướng dẫn
Tại điểm cao nhất của vòng xiếc có các lực tác dụng lên xe là trọng lực \[\overrightarrow{P}\] và phản lực \[\overrightarrow{Q}\] của vòng xiếc.
Ta có: \[P+Q={{F}_{ht}}=m\frac{{{v}^{2}}}{R}\Rightarrow Q=m\frac{{{v}^{2}}}{R}-P\]
Gọi \[\overrightarrow{N}\] là lực ép của người đi xe lên vòng xiếc, ta có:
\[N=Q=m\frac{{{v}^{2}}}{R}-mg=80.\frac{{{10}^{2}}}{8}-80.9,8=216N\]
Câu 11: Xe có khối lượng 1 tấn đi qua cầu vồng. Cầu có bán kính cong là 50 m. Giả sử xe chuyển động đều với vận tốc 10 m/s. Tại đỉnh cầu, tính lực nén của xe lên cầu. Lấy g = 9,8 m/s2.
A. 7200 N. B. 5500 N. C. 7800 N. D. 6500 N.
Hướng dẫn
Một phần trọng lực đóng vai trò là lực hướng tâm.
Tại điểm cao nhất áp lực ô tô lên mặt đường là
\[N=P-{{F}_{ht}}\Leftrightarrow N=mg-\frac{m{{v}^{2}}}{R}=100.9,8-\frac{{{100.10}^{2}}}{50}=7800N\]
Câu 12: Một xe có khối lượng 1600 kg chuyển động trên đường cua tròn có bán kính r = 100 m với vận tốc không đổi 72 km/h. Hỏi giá trị của hệ số ma sát giữa lốp xe và mặt đường ít nhất bằng bao nhiêu để xe không trượt. Lấy g = 10 m/s2.
A. 0,35. B. 0,26. C. 0,33. D. 0,4.
Hướng dẫn
72 km/h = 20 m/s.
Xe chuyển động tròn đều nên \[\overrightarrow{{{F}_{msn}}}\] đóng vai trò là lực hướng tâm.
Để xe không trượt trên đường thì \[{{F}_{ht}}\le {{F}_{msn}}\Rightarrow m\frac{{{v}^{2}}}{r}\le \mu mg\Rightarrow \mu \ge \frac{{{v}^{2}}}{gr}\]
\[\Rightarrow \mu \ge \frac{{{20}^{2}}}{100.10}=0,4\Rightarrow {{\mu }_{\min }}=0,4\]
Câu 13: Một máy bay thực hiện một vòng nhào lộn bán kính 400 m trong mặt phẳng thẳng đứng với vận tốc 540 km/h. Tìm lực do người lái có khối lượng 60 kg nén lên ghế ngồi ở điểm cao nhất và thấp nhất của vòng nhào. Lấy g = 10 m/s2.
A. 2775 N; 3975 N. B. 2552 N; 4500 N. C. 1850 N; 3220 N. D. 2680 N; 3785 N.
Hướng dẫn
Các lực tác dụng lên xe là trọng \[\overrightarrow{P}\] và phản lực \[\overrightarrow{Q}\] của vòng xiếc.
Tại vị trí cao nhất, ta có: \[P+Q={{F}_{ht}}=m\frac{{{v}^{2}}}{R}\Rightarrow Q=m\frac{{{v}^{2}}}{R}-P\]
Gọi \[\overrightarrow{N}\] là lực ép của người đi xe lên vòng xiếc, ta có:
\[N=Q=m\frac{{{v}^{2}}}{R}-mg=60.\frac{{{150}^{2}}}{400}-60.10=2775N\]
Tại vị trí thấp nhất, ta có: \[-P+Q={{F}_{ht}}=m\frac{{{v}^{2}}}{R}\Rightarrow Q=m\frac{{{v}^{2}}}{R}+P\]
Gọi \[\overrightarrow{N}\] là lực ép của người đi xe lên vòng xiếc, ta có:
\[N=Q=m\frac{{{v}^{2}}}{R}+mg=60.\frac{{{150}^{2}}}{400}+60.10=3975N\]
Câu 14: Người đi xe đạp ( khối lượng tổng cộng 60 kg) trên vòng xiếc bán kính 6,4 m phải đi qua điểm cao nhất với vận tốc tối thiểu bao nhiêu để không rơi.Cho g = 10 m/s2.
A. 15 m/s. B. 8 m/s. C. 12 m/s. D. 9,3 m/s.
Hướng dẫn
Tại điểm cao nhất của vòng xiếc có các lực tác dụng lên xe là trọng lực \[\overrightarrow{P}\] và phản lực \[\overrightarrow{Q}\] của vòng xiếc.
Ta có: \[P+Q={{F}_{ht}}=m\frac{{{v}^{2}}}{R}\Rightarrow Q=m\frac{{{v}^{2}}}{R}-P\]
Gọi \[\overrightarrow{N}\] là lực ép của người đi xe lên vòng xiếc, ta có:
\[N=Q=m\frac{{{v}^{2}}}{R}-mg\]
Muốn không bị rơi khỏi vòng xiếc, tức là vẫn còn lực ép lên vòng xiếc. Khi đó, \[N\ge 0\Rightarrow m\frac{{{v}^{2}}}{R}-mg\ge 0\].
\[\Rightarrow v\ge \sqrt{gR}=\sqrt{10.6,4}=8\left( m/s \right)\Rightarrow {{v}_{\min }}=8\left( m/s \right)\]
Câu 15: Một chiếc bàn tròn bán kính R = 35 cm , quay quanh trục thẳng đứng với vận tốc góc ω = 3 rad/s. Hỏi ta có thể đặt một vật nhỏ trên vùng nào của bàn mà vật không bị văng ra xa tâm bàn. Hệ số ma sát nghỉ giữa vật và mặt bàn là µn = 0,25.
A. 0,27 m. B. 0,35 m. C. 0,4 m. D. 0,56 m.
Hướng dẫn
Lực ma sát đóng vai trò là lực hướng tâm. Vật không bị văng ra xa tâm bàn khi \[{{F}_{ht}}\le {{F}_{ms}}\].
\[\Rightarrow \frac{m{{v}^{2}}}{r}\le \mu mg\Rightarrow m{{\omega }^{2}}r\le \mu mg\Rightarrow r\le \frac{\mu g}{{{\omega }^{2}}}=0,272m\]
Câu 16: Tính khoảng cách giữa tâm vệ tinh địa tĩnh của Trái Đất với tâm Trái Đất. Biết khối lượng của Trái Đất là M = 6,1024 kg. Chu kì quay của Trái Đất quanh trục của nó là 24 h. Hằng số hấp dẫn G = 6,67.10-11 Nm2/kg2.
A. 422980 km. B. 42298 km. C. 42982 km. D. 42982 m.
Hướng dẫn
Vận tốc dài của vệ tinh \[v=\omega .r=2\pi .\frac{1}{T}.r\]
Lực hấp dẫn đóng vai trò là lực hướng tâm.
\[\Rightarrow \frac{m{{v}^{2}}}{r}=\frac{GmM}{{{r}^{2}}}\Leftrightarrow \frac{4{{\pi }^{2}}{{r}^{2}}}{{{T}^{2}}}=\frac{GM}{r}\Rightarrow r=\sqrt[3]{\frac{GM{{T}^{2}}}{4{{\pi }^{2}}}}\]
Thay T = 24h = 86400 s; \[M={{6.10}^{24}}kg\], G vào \[\Rightarrow r=42298km\]
Câu 17: Lí do chính khi ô tô đi qua những đoạn đường có khúc cua thì phải đi chậm lại là
A. để ô tô không bị văng về phía tâm khúc cua.
B. để lực hướng tâm cần thiết giữ ô tô chuyển động tròn không quá lớn.
C. để lái xe có thể quan sát xe đi ngược chiều.
D. để tăng lực ma sát nghỉ cực đại giữ ô tô không bị văng ra khỏi đường.
Hướng dẫn
Khi ô tô qua những khúc cua thì lực ma sát đóng vai trò là lực hướng tâm.
\[{{F}_{ht}}=\frac{m{{v}^{2}}}{r};{{F}_{ms}}=\mu mg\]
Để ô tô không bị trượt thì \[{{F}_{ht}}\le {{F}_{ms}}\]
Nếu đến chỗ rẽ mà ô tô chay nhanh (v lớn) thì lực ma sát nghỉ cực đại không đủ lớn để đóng vai trò lực hướng tâm giữ ô tô chuyển động tròn, nên ô tô sẽ trượt li tâm văng ra khổi đường dễ gây tai nạn.
Câu 18: Một ô tô có khối lượng 1200 kg chuyển động đều qua một đoạn cầu vượt (coi là cung tròn) với vận tốc 36 km/h. Hỏi áp lực của ô tô vào mặt đường tại điểm cao nhất bằng bao nhiêu ? Biết bán kính cong của đoạn cầu vượt là 50 m. Lấy g = 10 m/s2.
A. 11950 N. B. 11760 N. C. 9600 N. D. 14400 N.
Hướng dẫn
36 km/h = 10 m/s.
Một phần trọng lực đóng vai trò là lực hướng tâm.
Tại điểm cao nhất áp lực ô tô lên mặt đường là \[N=P-{{F}_{ht}}\]
\[\Leftrightarrow N=mg-\frac{m{{v}^{2}}}{R}=1200.10-\frac{{{1200.10}^{2}}}{50}=9600N\]
Câu 19: Một tài xế điều khiển một ôtô có khối lượng 1000kgchuyển động quanh vòng tròn có bán kính 100m nằm trên một mặt phẳng nằm ngang với vận tốc có độ lớn là 10m/s. Lực ma sát cực đại giữa lốp xe và mặt đường là 900N. Ôtô sẽ
A. trượt vào phía trong của vòng tròn . B. trượt ra khỏi đường tròn.
C. chạy chậm lại vì tác dụng của lực li tâm. D. chưa đủ cơ sở để kết luận.
Hướng dẫn
Lực ma sát đóng vai trò là lực hướng tâm.
Ta có: \[{{F}_{ht}}=\frac{m{{v}^{2}}}{r}=\frac{{{1000.10}^{2}}}{100}=1000N>900N\]
\[\Rightarrow {{F}_{ht}}>{{F}_{ms\max }}\Rightarrow \] Ô tô sẽ trượt ra khỏi đường tròn.
Câu 20: Một vật nặng 4,0kg được gắn vào một dây thừng dài 2m. Nếu vật đó quay tự do thành một vòng tròn quanh trục thẳng đứng gắn với đầu dây thì sức căng của dây là bao nhiêu khi căng tối đa và vật có vận tốc 5 m/s?
A. 5,4 N. B. 10,8 N. C. 21,6 N. D. 50 N.
Hướng dẫn
Lực căng dây đóng vai trò là lực hướng tâm.
\[{{T}_{\max }}={{F}_{ht}}=\frac{m{{v}^{2}}}{R}=\frac{{{4.5}^{2}}}{2}=50\left( N \right)\]







