Bài tập nhiệt học nâng cao

A.Tóm tắt lý thuyết:

I./ Sự nở vì nhiệt:

1) Tính chất:

- Các chất (rắn, lỏng, khí) - nói chung - khi nóng thì nở ra, khi lạnh thì co lại.

- Đặc biệt, nước ở thể rắn (nước đá) thì thể tích tăng nên nổi trên mặt nước; khi tăng nhiệt độ từ 0⁰C đến 4⁰C thì co lại, chỉ khi tăng từ 4⁰C trở lên mới nở ra.

- Các chất (rắn, lỏng, khí) khác nhau thì nở vì nhiệt khác nhau.

- Chất khí nở vì nhiệt > chất lỏng > chất rắn.

- Các chất khi co dãn đều sinh ra một lực rất lớn.

2) Băng kép: gồm hai thanh kim loại khác chất (như đồng và thép) ghép chặt với nhau. Khi nóng băng kép sẽ cong lên: kim loại nở nhiều hơn (đồng) nằm ngoài, kim loại nở ít hơn (thép) nằm trong (phần lõm).

 

II./ Nhiệt độ -  Nhiệt kế - Nhiệt giai:

1) Nhiệt độ: Nhiệt độ của vât càng cao thì các nguyên tử, phân tử cấu tạo nên vật chuyển động càng nhanh.

2) Nhiệt kế:

- Là dụng cụ dùng để đo nhiệt độ.

          - Có nhiều loại: nhiệt kế y tế; nhiệt kế thuỷ ngân; nhiệt kế rượu (hay dầu)

3) Nhiệt giai: Có nhiều loại nhiệt giai:

- Nhiệt giai Xenxiut (⁰C): chọn nước đá đang tan là 0⁰C; hơi nước đang sôi là 100⁰C

- Nhiệt giai Farenhai (⁰F): chọn nước đá đang tan là 32⁰F; hơi nước đang sôi là 212⁰F

                    Suy ra: 1⁰C = 1,8⁰F     hay 1⁰F = 1/1,8 ⁰C

- Nhiệt giai Kenvin (K): chọn nước đá đang tan là 273K; hơi nước đang sôi là 373K

Suy ra 1⁰C = 1K

- Đổi ⁰C sang ⁰F và ⁰F sang ⁰C:

Ví dụ 1: Đổi 20⁰C sang ⁰F:

20⁰C  =       0⁰C    +       20⁰C

          =       32⁰F  +       (20 x 1,8⁰F) =        68⁰F

Ví dụ 2: Đổi 68⁰F sang ⁰C:

               68⁰F  =       32⁰F  +       36⁰F

                         =       0⁰C    +       (36/1,8 ⁰C)  =       20⁰C 

III./ Nhiệt năng:

Tổng động năng của các phân tử cấu tạo nên vật gọi là nhiệt năng của vật.

Có 2 cách làm thay đổi nhiệt năng: thực hiện công và truyền nhiệt.

IV./ Nhiệt lượng:

 Là phần nhiệt năng mà vật nhận thêm hay mất bớt trong quá trình truyền nhiệt.

Có 3 cách truyền nhiệt

1) Dẫn nhiệt:

- Là sự truyền nội năng từ hạt này sang hạt khác của vật.

          - Dẫn nhiệt chủ yếu xảy ra ở chất rắn.

- Kim loại dẫn nhiệt tốt nhất.

- Chất lỏng dẫn nhiệt kém (trừ dầu và thuỷ ngân).

- Chất khí dẫn nhiệt rất kém.

2) Đối lưu:

Là sự truyền nội năng bởi các dòng chất lỏng hay chất khí.

Dòng chất lỏng (hay khí) nóng từ dưới đi lên và dòng chất lỏng (hay khí) lạnh từ trên đi xuống.

3) Bức xạ nhiệt:

Là sự truyền nội năng bằng cách phát ra những tia nhiệt đi thẳng.

Các vật nóng đều phát ra các bức xạ nhiệt.

V./ Nhiệt dung riêng:

Nhiệt dung riêng của một chất cho biết nhiệt lượng cần truyền cho 1kg chất đó tăng thêm 1⁰C.

Ký hiệu:      C                 Đơn vị: J/kg.K               

Ví dụ: Nói nhiệt dung riêng của nước là 4200J/kg.K có nghĩa là

Muốn 1kg nước tăng thêm 1⁰C thì cần cung cấp một nhiệt lượng là 4200J

VI./ Công thức tính nhiệt lượng:

1) Công thức:                                     Q = m.C.Dt

Trong đó:    Q: nhiệt lượng thu vào (hay toả ra)     (J)

                   m: khối lượng vật                              (kg)

                   Dt: độ tăng (hay giảm) nhiệt độ           (⁰C)

• Nếu tính nhiệt lượng thu vào để tăng nhiệt độ:        Dt = t₂ – t₁
• Nếu tính nhiệt lượng toả ra để giảm nhiệt độ:          Dt = t₁ – t₂

Chú ý: Có nhiều bài toán ta không biết được vật tăng hay giảm nhiệt độ (vì bài toán chỉ cho ẩn số) ta tính:   Dt = t⁰_cuối – t⁰_đầu    

Lúc này Dt có thể dương hay âm => Q có thể dương hay âm.

• Nếu Q > 0: vật thu nhiệt
• Nếu Q < 0: vật toả nhiệt

2) Phương trình cân bằng nhiệt:         

• Nếu biết rõ vật nào toả nhiệt, vật nào thu nhiệt, ta dùng phương trình:

Q_toả = Q_thu                       (1)

• Nếu không biết rõ vật nào tỏa nhiệt và vật nào thu nhiệt, ta dùng phương trình định luật bảo toàn năng lượng:

Q₁ + Q₂ + Q₃ ... = 0         (2)

Trong đó Q₁; Q₂; Q₃ ... có thể dương hoặc âm

• Phương trình (1) chỉ áp dụng cho trường hợp có 2 vật: một vật nóng và một vật lạnh hơn.
• Phương trình (2) có thể áp dụng cho mọi trường hợp trao đổi nhiệt.

II./ Sự chuyển thể của các chất:

1. Sự nóng chảy và sự đông đặc:

a) Tính chất:

• Sự chuyển một chất từ thể rắn sang thể lỏng gọi là sự nóng chảy.
• Sự chuyển một chất từ thể lỏng sang thể rắn gọi là sự đông đặc.
• Một chất bắt đầu nóng chảy ở nhiệt độ nào thì cũng bắt đầu đông đặc ở nhiệt độ đó. Trong suốt thời gian nóng chảy (hay đông đặc) nhiệt độ của vật không thay đổi.
• Mỗi chất nóng chảy (hay đông đặc) ở một nhiệt độ nhất định. Nhiệt độ này gọi là nhiệt độ nóng chảy (hay nhiệt độ đông đặc) của chất ấy.

Ví dụ: Với nước là 0⁰C; với băng phiến là 80⁰C

b) Nhiệt nóng chảy:

Nhiệt lượng cần thiết cho 1kg chất rắn chuyển từ thể rắn sang thể lỏng ở nhiệt độ nóng chảy gọi là nhiệt nóng chảy của chất đó.

Ký hiệu: 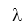           (lăm-đa)             Đơn vị:        J/kg

Ví dụ: Nói nhiệt nóng chảy của nước đá là l = 3,4 ´ 10⁵ J/kg

Nghĩa là: muốn cho 1kg nước đá ở 0⁰C hoá lỏng hết thì cần một nhiệt lượng là 3,4 ´ 10⁵ J

c) Công thức:                       Q = m.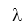

Trong đó:         Q: nhiệt lượng cần thiết                      (J)

                        m: khối lượng của vật                        (kg)

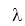                        : nhiệt nóng chảy của chất làm vật    (J/kg)

Chú ý: Nhiệt lượng vật toả ra khi đông đặc đúng bằng nhiệt lượng vật đó thu vào khi nóng chảy. Như vậy công thức Q = m.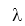 vẫn dùng được khi vật đông đặc, lúc này 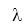được gọi là nhiệt đông đặc.

2. Sự hoá hơi và sự ngưng tụ:

1. Tính chất:

• Sự chuyển một chất từ thể lỏng sang thể hơi gọi là sự hoá hơi.
• Sự chuyển một chất từ thể hơi sang thể lỏng gọi là sự ngưng tụ.

• Sự bay hơi là sự hoá hơi chỉ xảy ra trên mặt thoáng chất lỏng.

Tốc độ bay hơi của chất lỏng phụ thuộc vào:

+ Nhiệt độ của chất lỏng: nhiệt độ càng cao, tốc độ bay hơi càng nhanh.

+ Diện tích mặt thoáng: diện tích càng rộng, tốc độ bay hơi càng nhanh.

+ Gió trên mặt thoáng: gió càng nhiều, tốc độ bay hơi càng nhanh.

+ Bản chất của chất lỏng: rượu bay hơi nhanh hơn nước, nước bay hơi nhanh hơn dầu.

• Sự sôi là sự hoá hơi xảy ra cả trên mặt thoáng và trong lòng chất lỏng.

+ Mỗi chất lỏng sôi ở một nhiệt độ nhất định. Nhiệt độ này gọi là nhiệt độ sôi hay điểm sôi.

+ Trong suốt thời gian sôi, nhiệt độ của chất lỏng không thay đổi.

+ Nhiệt độ sôi phụ thuộc áp suất trên mặt thoáng chất lỏng: áp suất tăng thì nhiệt độ sôi tăng; áp suất giảm thì nhiệt độ sôi giảm.

Ví dụ: Ở áp suất thường (1atm), nhiệt độ sôi của nước là 100⁰C; nếu áp suất 10 atm thì nhiệt độ sôi của nước 180⁰C; nếu áp suất 0,1 atm thì nước sôi ở 50⁰C.

b) Nhiệt hoá hơi:

Nhiệt lượng cần thiết cho 1kg chất chuyển từ thể lỏng sang thể hơi ở nhiệt độ sôi gọi là nhiệt hoá hơi của chất đó.

Ký hiệu:           L                 Đơn vị:        J/kg

Ví dụ: Nói nhiệt hoá hơi của nước là L = 2,3 ´ 10⁶ J/kg nghĩa là:

Muốn cho 1kg nước ở 100⁰C hoá hơi hoàn toàn cần cung cấp một nhiệt lượng là 2,3 ´ 10⁶ J

          c) Công thức:                  Q = m.L

          Trong đó:              Q: Nhiệt lượng cần thiết  (J)

                                       m: khối lượng vật           (kg)

                                      L: Nhiệt hoá hơi              (J/kg)

Chú ý: Nhiệt lượng vật toả ra khi ngưng tụ đúng bằng nhiệt lượng vật đó thu vào khi hoá hơi. Như vậy công thức Q = m.L vẫn dùng được khi vật ngưng tụ, lúc này L được gọi là nhiệt ngưng tụ.

VIII./ Năng suất toả nhiệt:

1. 1. 1.  Định nghĩa: Nhiệt lượng toả ra khi đốt cháy hoàn toàn 1kg nhiên liệu gọi là năng suất toả nhiệt của nhiên liệu đó.

Ký hiệu:          q                 Đơn vị:        J/kg

Ví dụ: Nói năng suất toả nhiệt của xăng là q = 4,6 ´ 10⁷ J/kg nghĩa là:

Đốt cháy hết 1kg xăng thì toả ra một nhiệt lượng là 4,6 ´ 10⁷ J

1. 1. 2.  Công thức:                     Q = m.q

Trong đó:                  Q: nhiệt lượng toả ra                                    (J)

                                 m: khối lượng nhiên liệu                              (kg)

                                 q: năng suất toả nhiệt của nhiên liệu đó        (J/kg)

IX./ Hiệu suất của động cơ nhiệt:

                                        

B. BÀI TẬP

I/ Các bài toán về sự trao đổi nhiệt của hai chất và nhiều chất

Phương pháp: Xác định các chất thu nhiệt, các chất tỏa nhiệt.

Áp dụng phương trình cân bằng nhiệt để thiết lập các phương trình cần thiết.

Bài 1. Người ta thả một thỏi đồng nặng 0, 4kg ở nhiệt độ 80⁰c vào 0, 25kg nước ở ${{t}_{o}}$= 18⁰c. Hóy xỏc định nhiệt độ cân bằng. Cho c$_{1}$= 400 j/kgk c$_{2}$= 4200 j/kgk

Giải . Gọi nhiệt độ khi cân bằng của hỗn hợp là t. Ta có phương trỡnh cõn bằng nhiệt của hỗn hợp như sau    ${{m}_{1}}.{{c}_{1}}.(80-t)={{m}_{2}}.{{c}_{2}}(t-18)$ 

Thay số vào ta cú  t  = 26,2⁰C

Bai 2: Người ta thả vào 0,2kg nước ở nhiệt độ 20⁰C một cục sắt có khối lượng 300g ở nhiệt độ 10⁰C và một miếng đồng có khối lượng 400g ở 25⁰C. Tính nhiệt độ cuối cùng của hỗn hợp và nêu rõ quá trình trao đổi nhiệt giữa các thành phần trong hỗn hợp đó. Cho c$_{1}$= 4200 j/kgk c$_{2}$= 460 j/kgk , c₃= 380 j/kgk

Giải . Gọi nhiệt độ khi cân bằng của hỗn hợp là t. Ta có phương trỡnh cõn bằng nhiệt của hỗn hợp như sau    m₁.c_1.(20 – t) +  m₃.c_3.(25 – t)  = m₂.c_2.(t – 10)

Thay số vào ta cú  t  = 20,31⁰C

Bài 3: Để có M = 500g nước ở nhiệt độ t = 18⁰C để pha thuốc rửa ảnh, người ta đẵ lấy nước cất ở t₁= 60⁰C trộn với nước cất đang ở nhiệt độ t₂= 4⁰C. Hoỉ đẵ dùng bao nhiêu nước nóng và bao nhiêu nước lạnh? Bỏ qua sự trao đổi nhiệt với vỏ bình.

Giải: Gọi khối lượng nước nóng phỉa dùng là m₁, KL nước lạnh phải dùng là m₂.

M = m₁ + m₂ = 0,5                                                              (1)

áp dụng pt: Q_tỏa = Q_thu ta được: m₂ = 3m₁                             (2)

Giải hệ ta được: m₁ = 0,125kg                                   m₂ = 0,375kg

Bài 4. Người ta thả một thỏi đồng nặng 0, 4kg ở nhiệt độ 80⁰c vào 0, 25kg nước ở ${{t}_{o}}$= 18⁰c. Hãy xác định nhiệt độ cân bằng. Cho c $_{1}$= 400 J/kgk c$_{2}$= 4200 J/kgk

Giải .

Gọi nhiệt độ khi cân bằng của hỗn hợp là t. Ta có phương trình cân bằng nhiệt của hỗn hợp như sau:

                                   ${{m}_{1}}.{{c}_{1}}.(80-t)={{m}_{2}}.{{c}_{2}}(t-18)$ 

Thay số vào ta có  t  = 26,2⁰C

Bài 5. Một hỗn hợp gồm ba chất lỏng không có tác dụng hoá học với nhau có khối lượng lần lượt là: ${{m}_{1}}=1kg,{{m}_{2}}=2kg,{{m}_{3}}=3kg.$Biết nhiệt dung riêng và nhiệt độ của chúng lần lượt là \[{{c}_{1}}=2000J/kgk,{{t}_{1}}={{10}^{0}}c,{{c}_{2}}=4000J/kgk,{{t}_{2}}={{10}^{0}}c,{{c}_{3}}=3000J/kgk,{{t}_{3}}={{50}^{0}}c\]. Hãy tính nhiệt độ hỗn hợp khi cân bằng

Tương tự bài toán trên ta tính ngay được nhiệt độ của hỗn hợp khi cân bằng là t

t = $\frac{{{m}_{1}}.{{c}_{1}}.{{t}_{1}}+{{m}_{2}}.{{t}_{2}}.{{c}_{2}}+{{m}_{3}}.{{c}_{3}}.{{t}_{3}}}{{{m}_{1}}.{{c}_{1}}+{{m}_{2}}.{{c}_{2}}+{{m}_{3}}.{{c}_{3}}}$ thay số vào ta có t = 20,5⁰C  

Từ đó ta có bài toán tổng quát như sau

Bài 6. Một hỗn hợp gồm n chất lỏng có khối lượng lần lượt là ${{m}_{1}},{{m}_{2}},......{{m}_{n}}$và nhiệt dung riêng của chúng lần lượt là ${{c}_{1}},{{c}_{2}}.......{{c}_{n}}$và nhiệt độ là ${{t}_{1}},{{t}_{2}}........{{t}_{n}}$. Được trộn lẩn vào nhau. Tính nhiệt độ của hỗn hợp  khi cân bằng nhiệt

Hoàn toàn tương tự bài toán trên ta có nhiệt độ cân bằng của hỗn hợp khi cân bằng nhiệt là:  

t = $\frac{{{m}_{1}}.{{c}_{1}}.{{t}_{1}}+{{m}_{2}}.{{t}_{2}}.{{c}_{2}}+{{m}_{3}}.{{c}_{3}}.{{t}_{3}}+........+{{m}_{n}}{{t}_{n}}{{c}_{n}}}{{{m}_{1}}.{{c}_{1}}+{{m}_{2}}.{{c}_{2}}+{{m}_{3}}.{{c}_{3}}+.........+{{m}_{n}}{{c}_{n}}}$

Bài 7: Người ta cho vòi nước nóng 70⁰C và vòi nước lạnh 10⁰C đồng thời chảy vào bể đã có sẳn 100kg nước ở nhiệt độ 60⁰C. Hỏi phải mở hai vòi trong bao lâu thì thu được nước có nhiệt độ 45⁰C. Cho biết lưu lượng của mỗi vòi là 20kg/phút. Bỏ qua sự mất mát năng lượng ra môi trường.

Giải:

Vì lưu lượng hai vòi chảy như nhau nên khối lượng hai loại nước xả vào bể bằng nhau. Gọi khối lượng mỗi loại nước là m(kg):

Ta có: m.c(70 – 45) + 100.c(60 – 45) = m.c(45 – 10)

      $\Leftrightarrow $         25.m    +      1500    =  35.m

      $\Leftrightarrow $                    10.m             = 1500      $\Rightarrow m=\frac{1500}{10}=150(kg)$

Thời gian mở hai vòi là:

$t=\frac{15}{20}=7,5(ph\acute{u}t)$

Bài 8: Một chiếc ca không có vạch chia được dùng để múc nước ở thùng chứa I và thùng chứa II rồi đổ vào thùng chứa III. Nhiệt độ của nước ở thùng chứa I là t₁ = 20 ⁰C, ở thùng II là t₂ = 80 ⁰C. Thùng chứa III đã có sẵn một lượng nước ở nhiệt độ t₃ = 40 ⁰C và bằng tổng số ca nước vừa đổ thêm. Cho rằng không có sự mất mát nhiệt lượng ra môi trường xung quanh. Hãy tính số ca nước cần múc ở thùng  I và thùng II để nước ở thùng III có nhiệt độ bằng 50 ⁰C ?

Giải:

Gọi m là khối lượng của mỗi ca nước,  n₁ là số ca nước ở thùng I,  n₂ là số ca nước ở thùng II  

Vậy số ca nước ở thùng III là n₁+ n₂,  nhiệt độ cân bằng của nước trong thùng III là 50⁰C   

Ta có :

     Nhiệt lượng thu vào của số nước từ thùng I là : Q₁ = m₁.c.(50-20) = n₁.m.c.30   (1)                                

    Nhiệt lượng tỏa ra của số nước từ thùng II là : Q₂ = m₂.c.(80-50) = n₂.m.c.30       (2)                                   

     Nhiệt lượng thu vào của số nước từ thùng III là :

 Q₃ =(n₁+n₂).m.c.(50 - 40) = (n₁+n₂).m.c.10    (3)                                    

     Do quá trình là cân bằng nên ta có : Q₁ + Q₃ = Q₂        (4)                        

Thay hệ thức (1), (2), (3) vào hệ thức (4) ta được: 2n₁= n₂                              

Như vậy nếu mức ở thùng II: n ca thì phải múc ở thùng I: 2n ca và số nước có sẵn trong thùng III là: 3n ca  (n nguyên dương )

Bài 9:  Trong một bình nhiệt lượng kế chứa hai lớp nước. Lớp nước lạnh ở dưới và lớp nước nóng ở trên. Tổng thể tích của hai khối nước này thay đổi như thế nào khi chúng sảy ra hiện tượng cân bằng nhiệt?. Bỏ qua sự trao đổi nhiệt với bình và với môi trường.

Giải: Gọi V₁; V₂; V’₁; V’₂ lần lượt là thể tích nước nóng, nước lạnh ban đầu và nước nóng, nước lạnh khi ở nhiệt độ cân bằng. độ nở ra hoặc co lại của nước khi thay đổi 1⁰C  phụ thuộc vào hệ số tỷ lệ K. sự thay đổi nhiệt độ của lớp nước nóng và nước lạnh lần lượt là ∆t₁ và ∆t₂.

                                     V₁ = V’₁ + V’₁K∆t₁  và V₂ = V’₂ - V’₂K∆t₂

       Ta có V₁ + V₂ = V’₁ + V’₂ + K(V’₁∆t₁  - V’₂∆t₂)

Theo phương trình cân bằng nhiệt thì: m₁C∆t₁ = m₂C∆t₂  với m₁, m₂ là khối lượng nước tương ứng ở điều kiện cân bằng nhiệt, vì cùng điều kiện nên chúng có khối lượng riêng như nhau

Nên: V’₁DC∆t₁ = V’₂DC∆t₂ Þ V’₁∆t₁ – V’₂∆t₂ = 0

Vậy: V₁ + V₂ = V’₁ + V’₂ nên tổng thể tích các khối nước không thay đổi

Bài 10: Trong một bình nhiệt lượng kế có chứa nước đá nhiệt độ t₁ = -5⁰C. Người ta đổ vào bình một lượng nước có khối lượng m = 0.5kg ở nhiệt độ t₂ = 80⁰C. Sau khi cân bằng nhiệt thể tích của chất chứa trong bình là V = 1,2 lít. Tìm khối lượng của chất chứa trong bình. Biết khối lượng riêng của nước và nước đá là D_n = 1000kg/m³ và D_d = 900kg/m³, nhiệt dung riêng của nước và nước đá là 4200J/kgK, 2100J/kgK, nhiệt nóng chảy của nước đá là 340000J/kg.

Giải: Nếu đá tan hết thì khối lượng nước đá là:      \[{{m}_{d}}=V.{{D}_{n}}-m=0,7\left( kg \right)\]

Nhiệt lượng cần cung cấp để nước đá tan hết là:     \[{{Q}_{1}}={{m}_{d}}{{c}_{d}}\left( 0-{{t}_{1}} \right)+\lambda {{m}_{d}}\] \[{{Q}_{1}}=7350+238000=245350\left( J \right)\]

Nhiệt lượng do nước toả ra khi hạ nhiệt độ từ 80⁰C đến 0⁰C là:

          \[{{Q}_{2}}=m.{{c}_{n}}\left( {{t}_{2}}-0 \right)=168000\left( J \right)\]

Nhận xét do Q₂ < Q₁nên nước đá không tan hết, đồng thời Q₂ > \[{{m}_{d}}{{c}_{d}}\left( 0-{{t}_{1}} \right)\] nên trong bình tồn tại cả nước và nước đá. Suy ra nhiệt độ khi cân bằng nhiệt là 0⁰C

Khối lượng nướcđá dã tan là:   \[{{m}_{d\tan }}=\frac{168000-7350}{340000}=0,4725\left( kg \right)\]

Sau khi cân bằng nhiệt:

Khối lượng nước trong bình là:   \[{{m}_{n}}=0,5+0,4725=0,9725\left( kg \right)\Rightarrow V=0,9725l\]

Thể tích nước đá trong bình là: \[{{V}_{d}}=V-{{V}_{n}}=1,2-0,9725=0,2275l\]

Khối lượng nước đá trong bình là: \[{{m}_{d}}^{'}={{V}_{d}}{{D}_{d}}=0,20475\left( kg \right)\]

Vậy khối lượng của chất trong bình là: \[m={{m}_{n}}+{{m}_{d}}^{'}=1,17725\left( kg \right)\]

Bài 11: Hai bình thông nhau chứa chất lỏng tới độ cao h. Bình bên phải có tiết diện không đổi là S. Bình bên trái có tiết diện là 2S tính tới độ cao h còn trên độ cao đó có tiết diện là S. Nhiệt độ của chất lỏng ở bình bên phải được giữ không đổi còn nhiệt độ chất lỏng ở bình bên trái tăng thêm  $\Delta {{t}^{0}}$C. Xác định mức chất lỏng mới ở bình bên phải. Biết rằng khi nhiệt độ tăng thêm 1⁰C thì thể tích chất lỏng tăng thên õ lần thể tích ban đầu. Bỏ qua sự nở của bình và ống nối.

Giải: Gọi D  là khối lượng riêng của nước ở nhiệt độ ban đầu. Khi tăng nhiệt độ thêm $\Delta {{t}^{0}}$C thì khối lượng riêng của nước là ${}^{D}/{}_{\left( 1+\beta \Delta t \right)}$. gọi mực nước dâng lên ở bình bên trái là $\Delta {{h}_{1}}$ và ở bình bên phải là $\Delta {{h}_{2}}$, do khối lượng nước được bảo toàn nên ta có:

                                    $\frac{D\left( 2Sh+S\Delta {{h}_{1}} \right)}{1+\beta \Delta t}+DS\left( h+\Delta {{h}_{2}} \right)=Dh\left( 2S+S \right)$       (1)

Khi nước trong bình ở trạng thái cân bằng thì áp suất tại hai đáy phải bằng nhau, ta có phương trình:

                                    $\frac{10.D\left( h+\Delta {{h}_{1}} \right)}{1+\beta \Delta t}=10D\left( h+\Delta {{h}_{2}} \right)$         (2)

 Từ (1) và (2) Ta có $\Delta {{h}_{2}}=\frac{h.\beta .\Delta t}{2\left( 1+\beta \Delta t \right)}=\frac{h.\beta .\Delta t}{2}$  bỏ qua $\beta .\Delta t$ở mẫu vì $\beta .\Delta t$<<1                                     

Do đó mực nước ở bình phải là:${{h}_{2}}=h+\Delta {{h}_{2}}=h\left( 1+\frac{\beta .\Delta t}{2} \right)$       

Bài 12: Một bình cách nhiệt chứa đầy nước ở nhiệt độ t₀ = 20⁰C. Người ta thả vào bình một hòn bi nhôm ở nhiệt độ t = 100⁰C, sau khi cân bằng nhiệt thì nhiệt độ của nước trong bình là t₁= 30,3⁰C. Người ta lại thả hòn bi thứ hai giống hệt hòn bi trên thì nhiệt độ của nước khi cân bằng nhiệt là t₂= 42,6⁰C. Xác định nhiệt dung riêng của nhôm. Biết khối lượng riêng của nước và nhôm lần lượt là 1000kg/m³ và 2700kg/m³, nhiệt dung riêng của nước là 4200J/kgK.

Giải:

Gọi V_n là thể tích của nước chứa trong bình, V_b thể tích của bi nhôm, khối lượng riêng của nước và nhôm lần lượt là D_n và D_b, nhiệt dung riêng lần lượt là C_n và C_b

Vì bình chứa đầy nước nên khi thả bi nhôm vào lượng nước tràn ra có thể tích bằng thể tích bi nhôm: V_t = V_b. Ta có phương trình cân bằng nhiệt thứ nhất là:

${{m}_{b}}{{C}_{b}}\left( t-{{t}_{1}} \right)=m_{n}^{'}{{C}_{n}}\left( {{t}_{1}}-{{t}_{0}} \right)$ ( Trong đó $m_{n}^{'}$ khối lượng nước còn lại sau khi thả viên bi thứ nhất )

${{V}_{b}}{{D}_{b}}{{C}_{b}}\left( t-{{t}_{1}} \right)=\left( {{V}_{n}}-{{V}_{b}} \right){{D}_{n}}{{C}_{n}}\left( {{t}_{1}}-{{t}_{0}} \right)$. Thay số vào ta có

${{V}_{b}}\left( 188190{{C}_{b}}+43260000 \right)=43260000{{V}_{n}}$  (1)

Khi thả thêm một viên bi nữa thì phương trình cân bằng nhiệt thứ hai:

$\left( m_{n}^{''}{{C}_{n}}+{{m}_{b}}{{C}_{b}} \right)\left( {{t}_{2}}-{{t}_{1}} \right)={{m}_{b}}{{C}_{b}}\left( t-{{t}_{2}} \right)$( Trong đó $m_{n}^{''}$khối lượng nước còn lại sau khi thả viên bi thứ hai )

$\left( {{V}_{n}}-2{{V}_{b}} \right){{D}_{n}}{{C}_{n}}\left( {{t}_{2}}-{{t}_{1}} \right)+{{m}_{b}}{{C}_{b}}\left( {{t}_{2}}-{{t}_{1}} \right)={{V}_{b}}{{D}_{b}}\left( t-{{t}_{2}} \right)$

Thay số vào ta có:

${{V}_{b}}\left( 121770{{C}_{b}}+{{10332.10}^{4}} \right)={{5166.10}^{4}}{{V}_{n}}$  (2)

Lấy (1) chia cho (2) Þ C_b =501,7 ( J/kgK)

Bài 13:. Người ta bỏ một miếng hợp kim chì và kẽm có khối lượng 50g ở nhiệt độ 136^oC vào một nhiệt lượng kế chứa 50g nước ở 14^oC. Hỏi có bao nhiêu gam chì và bao nhiêu gam kẽm trong miếng hợp kim trên? Biết rằng nhiệt độ khi có cân bằng nhiệt là 18^oC và muốn cho riêng nhiệt lượng kế nóng thêm lên 1^oC thì cần 65,1J; nhiệt dung riêng của nước, chì và kẽm lần lượt là 4190J/(kg.K), 130J/(kg.K) và 210J/(kg.K). Bỏ qua sự trao đổi nhiệt với môi trường bên ngoài.

- Gọi khối lượng của chì và kẽm lần lượt là m_c và m_k, ta có:

                                                   m_c + m_k = 0,05(kg).                    (1)

- Nhiệt lượng do chì và kẽm toả ra: \[{{\text{Q}}_{\text{1}}}\text{ = }{{\text{m}}_{\text{c}}}{{\text{c}}_{\text{c}}}\text{(136 - 18) = 15340}{{\text{m}}_{\text{c}}}\];

                                                      \[{{\text{Q}}_{\text{2}}}\text{ = }{{\text{m}}_{\text{k}}}{{\text{c}}_{\text{k}}}\text{(136 - 18) = 24780}{{\text{m}}_{\text{k}}}\].

- Nước và nhiệt lượng kế thu nhiệt lượng là: 

     \[{{\text{Q}}_{\text{3}}}\text{ =  }{{\text{m}}_{\text{n}}}{{\text{c}}_{\text{n}}}\text{(18 - 14) = 0,05}\times \text{4190}\times \text{4 = 838(J)}\]

     \[{{\text{Q}}_{\text{4}}}\text{ =  65,1}\times \text{(18 - 14) = 260,4(J)}\].

- Phương trình cân bằng nhiệt: \[{{\text{Q}}_{\text{1}}}\text{ + }{{\text{Q}}_{\text{2 }}}\text{= }{{\text{Q}}_{\text{3}}}\text{ + }{{\text{Q}}_{\text{4}}}\]  \[\Rightarrow \]

                                            15340m_c + 24780m_k = 1098,4          (2)

- Giải hệ phương trình (1) và (2) ta có: m_c $\approx $ 0,015kg; m_k $\approx $ 0,035kg.

                                Đổi ra đơn vị gam: m_c $\approx $ 15g; m_k $\approx $ 35g

II/  Các bài toán có sự chuyển thể của các chất

Bài 1. Bỏ 100g nước đá ở ${{t}_{1}}={{0}^{o}}C$ vào 300g nước ở ${{t}_{2}}={{20}^{o}}C$

Nước đá có tan hết không? Nếu không hãy tính khối lượng đá còn lại . Cho nhiệt độ nóng chảy của nước đá là $\lambda =3,{{4.10}^{5}}j/kgk$và nhiệt dung riêng của nước là 

c = 4200J/kg.k $$

Giải.

Gọi nhiệt lượng của nước là ${{Q}_{t}}$từ 20⁰C về 0⁰C$_{{}}$và của nước đá tan hết là Q thu ta có

${{Q}_{t}}$= ${{m}_{2}}{{c}_{2}}.(20-0)$= 0,3.4200.20 =25200J

${{Q}_{thu}}={{m}_{1}}.\lambda $ = 0,1.$3,{{4.10}^{5}}$= 34000J

Ta thấy Q thu > Qtoả nên nước đá không tan hết. Lượng nước đá chưa tan hết là $m=\frac{{{Q}_{thu}}-{{Q}_{toa}}}{\lambda }$  = $\frac{8800}{3,{{4.10}^{5}}}$= 0,026 kg

Bài 2. Trong một bình có chứa ${{m}_{1}}=2kg$nước ở ${{t}_{1}}={{25}^{0}}c$. Người ta thả vào bình ${{m}_{2}}kg$nước đá ở ${{t}_{2}}$= $-{{20}^{0}}c$. Hảy tính nhiệt độ chung của hỗn hợp khi có cân bằng nhiệt trong các trường hợp sau đây:

a) ${{m}_{2}}$= 1kg

b) ${{m}_{2}}$= 0,2kg

c) ${{m}_{2}}$ = 6kg

cho nhiệt dung riêng của nước, của nước đá và nhiệt nóng chảy của nước đá lần lượt là     \[{{c}_{1}}=4,2kJ/kgk;{{c}_{2}}=2,1kJ/kgk,\lambda =340kJ/kg\]

Giải

Nếu nước hạ nhiệt độ tới 0⁰c thì nó toả ra một nhiệt lượng

${{Q}_{1}}={{c}_{1}}{{m}_{1}}({{t}_{1}}-0)=4,2.2.(25-0)=210kj$

a) ${{m}_{2}}$= 1kg

Nhiệt lượng cần cung cấp để nước đá tăng nhiệt độ tới o^oc

${{Q}_{2}}={{c}_{2}}{{m}_{2}}(o-{{t}_{2}})=2,1.(o-(-20))=42kj$

${{Q}_{1}}\rangle {{Q}_{2}}$ nước đá bị nóng chảy.

Nhiệt lượng để nước đá nóng chảy hoàn toàn:

$Q{{'}_{2}}=\lambda .{{m}_{2}}=340.1=340kj$

${{Q}_{1}}\langle {{Q}_{2}}+Q{{'}_{2}}$  nước đá chưa nóng chảy hoàn toàn. Vậy nhiệt độ cân bằng là 0⁰C. Khối lượng nước đá đã đông đặc là ${{m}_{y}}$

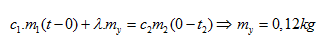
Khối lượng nước đá đã nóng chảy ${{m}_{x}}$được xác định bởi:

${{c}_{1}}.{{m}_{1}}(t-0)={{c}_{2}}{{m}_{2}}(0-{{t}_{2}})+\lambda .{{m}_{x}}\Rightarrow {{m}_{x}}\approx 0,5kg$

Khối lượng nước có trong bình: ${{m}_{n}}={{m}_{1}}+{{m}_{x}}\approx 2,5kg$

Khối lượng nước đá còn lại ${{m}_{d}}={{m}_{2}}-{{m}_{x}}=0,5kg$

b) ${{m}_{2}}=0,2kg$: tính tương tự như ở phần a .

${{Q}_{2}}={{c}_{2}}{{m}_{2}}(0-{{t}_{2}})=8400j;Q{{'}_{2}}=\lambda .{{m}_{2}}=68000j$

${{Q}_{1}}\rangle {{Q}_{2}}+Q{{'}_{2}}$ nước đá đã nóng chảy hết và nhiệt độ cân bằng cao hơn O^oc. Nhiệt độ cân bằng được xác định từ

${{c}_{2}}{{m}_{2}}(0-{{t}_{2}})+\lambda .{{m}_{2}}+{{c}_{1}}{{m}_{2}}(t-0)={{c}_{1}}{{m}_{1}}({{t}_{1}}-t)$

Từ đó $t\approx 14,{{5}^{0}}c$

Khối lượng nước trong bình: ${{m}_{n}}={{m}_{1}}+{{m}_{2}}=2,2kg$

Khối lượng nước đá ${{m}_{d}}=O$

c) ${{m}_{2}}=6kg$

${{Q}_{2}}={{c}_{2}}{{m}_{2}}(0-{{t}_{2}})=252kj$

${{Q}_{1}}\langle {{Q}_{2}}$: nước hạ nhiệt độ tới O^ocvà bắt đầu đông đặc.

Nếu  nước đông đặc hoàn toàn thì nhiệt lượng toả ra là:

                               $Q{{'}_{1}}=\lambda {{m}_{1}}=680kj$

${{Q}_{2}}\langle {{Q}_{1}}+Q{{'}_{1}}$: nước chưa đông đặc hoàn toàn, nhiệt độ cân bằng là O^oc

Khối lượng nước đá có trong bình khi đó:

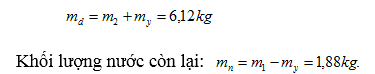
Bài 3: Trong một cục nước đá lớn ở 0⁰C có một cái hốc với thể tích V = 160cm³ . Người ta rốt vào hốc đó 60g nước ở nhiệt độ 75⁰C. Hỏi khi nước nguội hẳn thì thể tích hốc rỗng còn lại bao nhiêu? Cho khối lượng riêng của nước và nước đá lần lượt là D_n = 1g/cm³,

D_d = 0,9g/cm³. Nhiệt nóng chảy của nước đá là: l = 3,36.10⁵ J/kg.

Giải:

Do khối đá lớn ở 0⁰C nên khi đổ 60g nước vào thì nhiệt độ của nước là 0⁰C. Nhiệt lượng do nước toả ra để nguội đến 0⁰C là: $Q=m.c.\Delta t=0,06.4200.75=18900J$

Nhiệt lượng này làm tan một lượng nước đá là: $m=\frac{Q}{\lambda }=\frac{18900}{3,{{36.10}^{5}}}=0,05625kg=56,25g$

Thể tích phần đá tan là:  ${{V}_{1}}=\frac{m}{{{D}_{d}}}=\frac{56,25}{0,9}=62,5c{{m}^{3}}$

Thể tích của hốc đá bây giờ là ${{V}^{'}}=V+{{V}_{1}}=160+62,5=222,5c{{m}^{3}}$

Trong hốc chứa lượng nước là:$\left( 60+56,25 \right)$ lượng nước này có thể tích là$116,25c{{m}^{3}}$ Vậy thể tích của phần rỗng là:       $222,5-116,25=106,25c{{m}^{3}}$

Bài 4: Trong một bình thành mỏng thẳng đứng diện tích đáy S = 100cm³ chứa nước và nước đá ở nhiệt độ t₁= 0⁰C, khối lượng nước gấp 10 lần khối lượng nước đá. Một thiết bị bằng thép

được đốt nóng tới t₂ = 80⁰C rồi nhúng ngập trong nước, ngay sau đó mức nước trong bình dâng lên cao thêm h = 3cm. Tìm khối lượng của nước lúc đầu trong bình biết rằng khi trạng thái cân bằng nhiệt được thiết lập trong bình nhiệt độ của nó là t = 5⁰C. Bỏ qua sự trao đổi nhiệt với bình và môi trường. Cho biết nhiệt dung riêng của nước là 4200J/kgK, của nước đá là 2100J/kgK, của thép là 500J/kgK. Nhiệt nóng chảy của nước đá là 330KJ/Kg , khối lượng riêng của thép là 7700kg/m³.

Giải:

Gọi khối lượng nước đá trong bình lúc đầu là m₀ thì khối lượng nước trong bình là 10m₀

Thể tích của khối thép đúng bằng thể tích nước bị chiếm chỗ:

                                           ${{V}_{t}}=h.S=3.100=300c{{m}^{3}}=0,{{3.10}^{-3}}{{m}^{3}}$ 

Khối lượng của khối thép:   ${{m}_{t}}={{D}_{t}}.{{V}_{t}}=0,{{3.10}^{-3}}.7700=2,31kg$

Phương trình cân bằng nhiệt :

                                           

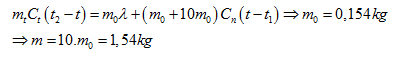
Bài 5: Trong một bình thí nghiệm có chứa nước ở 0⁰C. Rút hết không khí ra khỏi bình, sự bay hơi của nước sảy ra khi hoá đá toàn bộ nước trong bình. Khi đó bao nhiêu phần trăm của nước đã hoá hơi nếu không có sự truyền nhiệt từ bên ngoài bình. Biết rằng ở 0⁰C 1kg nước hoá hơi cần một nhịêt lượng là 2543.10³J và để 1kg nước đá nóng chảy hoàn toàn ở 0⁰C cần phải cung cấp lượng nhiệt là 335,2.10³J.

Giải:Gọi khối lượng nước ở 0⁰C là m, khối lượng nước hoá hơi là Dm thì khối lượng nước hoá đá là ( m -  Dm )

Nước muốn hoá hơi phải thu nhiệt: Q₁ = Dm.l = 2543.10³Dm

Nước ở 0⁰ hoá đá phải toả ra một nhiệt lượng: Q₂ = 335.10³( m -  Dm )

Theo định luật bảo toàn năng lượng ta có Q₁ = Q₂

                                 $\frac{\Delta m}{m}=\frac{335,2}{2878,2}=11,65$%

Bài 6 : Trong một bình nhiệt lượng kế chứa hai lớp nước: Lớp nước lạnh ở dưới, lớp nước nóng ở trên. Thể tích của cả hai khối nước có thay đổi không khi sảy ra cân bằng nhiệt? Hãy chứng minh khẳng định trên. Bỏ qua sự trao đổi nhiệt với thành bình.

Giải: Gọi V₁, V₂ là thể tích  ban đầu của nước nóng và nước lạnh, V₁^’ và V₂^’ là thể tích nước nóng và nước lạnh ở nhiệt độ cân bằng t_cb , ỏ là hệ số nở của nước.

Thể tích V₁ ở nhiệt độ ban đầu là: ${{V}_{1}}=V_{1}^{'}\left( 1+\alpha .\Delta {{t}_{1}} \right)\left( 1 \right)$ do t₁> t_cb

Thể tích V₂ ở nhiệt độ ban đầu là: ${{V}_{2}}={{V}_{2}}_{{}}^{'}\left( 1-\alpha \Delta {{t}_{2}} \right)\left( 2 \right)$ do t₂< t_cb

Từ (1) và (2) ta có: ${{V}_{1}}+{{V}_{2}}=V_{1}^{'}+V_{2}^{'}+\alpha \left( V_{1}^{'}.\Delta {{t}_{1}}-V_{2}^{'}.\Delta {{t}_{2}} \right)\left( 3 \right)$

Theo phương trình cân bằng nhiệt ta có:              ${{m}_{1}}{{c}_{{}}}\Delta {{t}_{1}}={{m}_{2}}c\Delta {{t}_{2}}$

                                                                           $V_{1}^{'}Dc\Delta {{t}_{1}}=V_{2}^{'}Dc\Delta {{t}_{2}}$

m₁ và m₂ cùng khối lượng riêng vì cùng là chất lỏng ở nhiệt độ cân bằng

ta có   $V_{1}^{'}\Delta {{t}_{1}}=V_{2}^{'}\Delta {{t}_{2}}\Rightarrow V_{1}^{'}\Delta {{t}_{1}}-V_{2}^{'}\Delta {{t}_{2}}=0$ (4)

 Thay (4) vào (3) ta có: ${{V}_{1}}+{{V}_{2}}=V_{1}^{'}+V_{2}^{'}$. Vậy thể tích hai khối nước không thay đổi khi đạt nhiệt độ cân bằng.

Bài 7: Người ta đặt một viên bi đặc bằng sắt bán kính R = 6cm đã được nung nóng tới nhiệt độ t = 325⁰C lên một khối nước đá rất lớn ở 0⁰C . Hỏi viên bi chui vào nước đá đến độ sâu là bao nhiêu? Bỏ qua sự dẫn nhiệt của nước đá và sự nóng lên của đá đã tan. Cho khối lượng riêng của sắt là D = 7800kg/m³, của nước đá là D₀ = 915kg/m³. Nhiệt dung riêng của sắt là C = 460J/kgK, nhiệt nóng chảy của nước đá là 3,4.10⁵J/kg. Thể tích khối cầu được tính theo công thức V = $\frac{4}{3}\pi .{{R}^{3}}$ với R là bán kính.

Giải: Khối lượng của nước đá lớn hơn rất nhiều khối lượng của bi nên khi có sự cân bằng nhiệt thì nhiệt độ là 0⁰C.

Nhiệt lượng mà viên bi tỏa ra để hạ xuống 0⁰C là: ${{Q}_{1}}=V.D.C\left( t-0 \right)=\frac{4}{3}\pi {{R}^{3}}D.C.t$

Giả sử có m (kg) nước đá tan ra do thu nhiệt của viên bi thì nhiệt lượng được tính theo công thức : ${{Q}_{2}}=m.\lambda $. Áp dụng phương trình cân bằng nhiệt ta có

         ${{Q}_{1}}={{Q}_{2}}\Rightarrow m=\frac{4.\pi .{{R}^{3}}.D.C.t}{3.\lambda }$ Thể tích khối đá tan ra là: ${{V}_{t}}=\frac{m}{{{D}_{0}}}$= $\frac{4.\pi .{{R}^{3}}.D.C.t}{3.\lambda }$.$\frac{1}{{{D}_{0}}}$

Do V_t là tổng thể tích của một hình trụ có chiều cao là h và một nửa hình cầu bán kính R nên  ta có  $h=\left( {{V}_{t}}-\frac{1}{2}.\frac{4}{3}\pi .{{R}^{3}} \right)\frac{1}{\pi .{{R}^{2}}}=\left( \frac{4RDCt}{3\lambda {{D}_{0}}}-\frac{2R}{3} \right)=\frac{2R}{3}\left( \frac{2DCt}{\lambda {{D}_{0}}}-1 \right)$

Vậy viên bi chui vào đến độm sâu là H = h + R thay số ta có H = 32 cm

III/ Các bài toán có sự trao đổi nhiệt với môi trường

Sự trao đổi nhiệt với môi trường luôn tỷ lệ với độ chênh lệch nhiệt độ. Tỷ lệ với diện tích tiếp xúc với môi trường. Nên nhiệt lượng hao phí ra môi trường là k.S.(t₂ - t₁) với k là hệ số tỷ lệ.

Trong trường hợp nhiệt lượng cung cấp cho vật không đủ làm cho vật chuyển thể thì khi vật có nhiệt độ ổn định ta luôn có công suất tỏa nhiệt ra môi trường đúng bằng công suất của thiết bị đốt nóng cung cấp cho vật.

Bài 1: Có ba bình hình trụ chỉ khác nhau về chiều cao. Dung tích các bình là 1l, 2l, 4l. tất cả đều chứa đầy nước. Nước trong các bình được đun nóng bởi thiết bị đun. Công suất thiết bị đun không đủ để nước sôi. Nước ở bình thứ nhất được đốt nóng đến 80⁰c. ở bình thứ hai tới 60⁰c. Nước ở bình thứ 3 được đốt nóng tới nhiệt độ nào? Nếu nhiệt độ phòng là 20⁰c. Cho rằng nhiệt lượng tỏa ra môi trường tỷ lệ với hiệu nhiệt độ giữa nước và môi trường xung quanh, tỷ lệ với diện tích tiếp xúc giữa nước và môi trường. Nước trong bình được đốt nóng đều đặn.

Giải: Gọi nhiệt độ của nước trong bình 1, 2, 3 khi ổn định nhiệt độ là T₁, T₂, T₃ và nhiệt độ phòng là T. Diện tích hai đáy bình là S và diện tích xung quanh của các bình tương ứng là S₁^; S₂; S₃. Dung tích các bình tương ứng là V₁; V₂; V₃

Vì: V₃ = 2V₂ = 4V₁ Nên S₃ = 2S₂ = 4S₁

Vì nhiệt độ tỏa ra môi trường tỷ lệ với độ chênh lệch nhiệt độ và tỷ lệ với diện tích tiếp xúc. Nên công suất hao phí của thiết bị đun của các bình tương ứng là:

                                   P_hp1 = A(S₁ + S)(T₁-T) = A($\frac{1}{4}$S₃ +S)60

                                   P_hp2 = A(S₂ + S)(T₂-T) = A($\frac{1}{2}$S₃ +S)40

                                   P_hp3 = A(S₃ + S)(T₃-T) = A( S₃ +S)(T₃ - 20)

Với A là hệ số tỷ lệ.

Nhiệt độ của các bình sẽ ổn định khi công suất cung cấp của thiết bị đun đúng bằng công suất hao phí. Nên:  A($\frac{1}{4}$S₃ +S)60 = A($\frac{1}{2}$S₃ +S)40    Þ  S₃ = 4S

Từ: A($\frac{1}{4}$S₃ +S)60 = A( S₃ +S)(T₃ - 20) và S₃ = 4S ta tính được T₃ = 44⁰C

Bài 2: Người ta thả một chai sữa của trẻ em vào phích đựng nước ở nhiệt độ t = 40⁰C. Sau khi đạt cân bằng nhiệt, chai sữa nóng tới nhiệt độ t₁ = 36⁰C, người ta lấy chai sữa này ra và tiếp tục thả vào phích một chai sữa khác giống như chai sữa trên. Hỏi chai sữa này khi cân bằng sẽ được làm nóng tới nhiệt độ nào? Biết rằng trước khi thả vào phích, các chai sữa đều có nhiệt độ t₀ =18⁰C.

Giải: Gọi q₁ là nhiệt lượng do phích nước toả ra để nó hạ 1⁰C , q₂ là nhiệt lượng cung cấp cho chai sữa để nó nóng thêm 1⁰C , t₂ là nhiệt độ của chai sữa thứ hai khi cân bằng.

Theo phương trình cân bằng nhiệt ta có:

              + Lần 1:                       q₁(t – t_­1) = q₂(t₁ ­- t₀)                                                               

              + Lần 2:                      q₁(t₁ – t_­2) = q₂(t₂ ­- t₀)                                                                 

              + Từ (1) và (2) giải ra ta có                        t₂=32,7⁰C

Bài 3: Một lò sưởi giữ cho phòng ở nhiệt độ 20⁰C khi nhiệt độ ngoài trởi là 5⁰C. Nếu nhiệt độ ngoài trời hạ xuống -5⁰C thì phải dùng thêm một lò sưởi nữa có công suất là 0,8kW mới duy trì được nhiệt độ của phòng như trên. Tìm công suất của lò sưởi đặt trong phòng.

Giải:

Gọi công suất của lò sưởi đặt trong phòng là P. Khi nhiệt độ trong phòng ổn định thì công suất của lò bằng công suất toả nhiệt do phòng toả ra môi trường. Ta có

                          P = q(20 – 5) =15q (1)trong đó q là hệ số tỉ lệ

Khi nhiệt độ ngoài trời giảm đi tới -5⁰C ta có:

                          ( P + 0,8 ) = q (20 – ( -5_{_})) = 25q (2)

Từ (1) và (2) ta có P = 1,2kW

IV/ Các bài toán có liên quan đến công suất tỏa nhiệt của các vật tỏa nhiệt.

Bài 1:

Một lò sưởi giữ cho phòng ở nhiệt độ 20⁰C khi nhiệt độ ngoài trời là 5⁰C. Nếu nhiệt độ ngoài trời hạ xuống tới – 5⁰C thì phải dùng thêm một lò sưởi nữa có công suất 0,8KW mới duy trì nhiệt độ phòng như trên. Tìm công suất lò sưởi được đặt trong phòng lúc đầu?.

Giải:  Gọi công suất lò sưởi trong phòng ban đầu là P, vì nhiệt toả ra môi trường tỷ lệ với độ chênh lệch nhiệt độ, nên gọi hệ số tỷ lệ là K. Khi nhiệt độ trong phòng ổn định thì công suất của lò sưởi bằng công suất toả nhiệt ra môi trường của phòng. Ta có: P = K(20 – 5) = 15K    ( 1)

Khi nhiệt độ ngoài trời giảm tới -5⁰C thì:(P + 0,8) = K[20 – (-5)] = 25K   (2)

Từ (1) và (2) ta tìm được P = 1,2 KW.

Bài 2: Một ấm điện bằng nhôm có khối lượng 0,5kg chứa 2kg   nước ở 25^oC. Muốn đun sôi lượng nước đó trong 20 phút thì ấm phải có công suất là bao nhiêu? Biết rằng nhiệt dung riêng của nước là C = 4200J/kg.K. Nhiệt dung riêng của nhôm là C₁ = 880J/kg.K và 30% nhiệt lượng toả ra môi trường xung quanh

Giải:    + Nhiệt lượng cần để tăng nhiệt độ của ấm nhôm từ 25^oC tới 100^oC là:      

                          Q₁ = m₁c₁ ( t₂ – t₁ ) = 0,5.880.(100 – 25 ) = 33000 ( J )                                   

             + Nhiệt lượng cần để tăng nhiệt độ của nước từ 25^oC tới 100^oC là:

                          Q₂ = mc ( t₂ – t₁ ) = 2.4200.( 100 – 25 ) = 630000 ( J )         

             + Nhiệt lượng tổng cộng cần thiết:

                          Q = Q₁ + Q₂ = 663000  ( J )      ( 1 )                                    

             + Mặt khác nhiệt lượng có ích để đun nước do ấm điện cung cấp trong thời gian 20 phút

                           Q = H.P.t                              ( 2 )                                     

( Trong đó H = 100% - 30% = 70%   ;   P là công suất của ấm   ;   t = 20 phút = 1200 giây )

               +Từ ( 1 ) và ( 2 ) : P = \[\frac{Q}{H.t}=\frac{663000.100}{70.1200}=789,3(\text{W)}\]

 

Bài 3: Trong một xi lanh thẳng đứng dưới một pít tông rất nhẹ tiết diện S = 100cm²có chứa M = 1kg nước ở 0⁰C. Dưới xi lanh có một thiết bị đun công suất P = 500W. Sau bao lâu kể từ lúc bật thiết bị đun pít tông sẽ được nâng lên thêm h = 1m so với độ cao ban đầu? Coi chuyển động của pít tông khi lên cao là đều , hãy ước lượng vận tốc của pít tông khi đó. Cho biết nhiệt dung riêng của nước là 4200J/ kg K,nhiệt hoá hơi của nước là 2,25.10⁶J/kg, khối lượng riieng của hơi nước ở nhiệt độ 100⁰C và áp suất khí quyển là 0,6kg/m³. Bỏ qua sự mất mát nhiệt bởi xi lanh và môi trường.

Giải:

Coi sự nở vì nhiệt và sự hoá hơi không làm thay đổi mức nước. Khi pít tông ở độ cao h thể tích nước là V = S.h = 0,01m³

Nhiệt lượng cần cung cấp để  nước nóng từ 0⁰C lên tới 100⁰C và hoá hơi ở 100⁰C là       $Q=mc\Delta t+lDV=419KJ+13,5KJ=432,5KJ$

Do bỏ qua sự mất mát nhiệt nên     $Q=Pt\Rightarrow t=\frac{Q}{P}=865\left( s \right)$

Thời gian đó gồm 2 giai đoạn thời gian đun sôi t₁ và thời gian hoá hơi t₂

                                                          t = t₁ + t₂

Do công suất đun không đổi nên $\frac{{{t}_{1}}}{{{t}_{2}}}=\frac{mc\Delta t}{lDV}=31$

                                                    Vậy ${{t}_{2}}=\frac{1}{32}t\approx 27\left( s \right)$

Vận tốc của pít tông tính từ lúc hoá hơi là $v=\frac{h}{{{t}_{2}}}\approx 3,7\left( cm/s \right)$

Bài 4: Muốn có 100 lít nước ở nhiệt độ 35⁰C thì phải đổ bao nhiêu lít nước đang sôi vào bao nhiêu lít nước ở nhiệt độ 15⁰C. Lấy nhiệt dung riêng của nước là 4190J/kg.K ?

Gỉải:

Gọi x là khối lượng nước ở 15⁰C và y là khối lượng nước đang sôi.

Ta có:

         x + y = 100kg       (1)

Nhiệt lượng y kg nước đang sôi toả ra:

         Q₁= y.4190.(100 - 35)

Nhiệt lượng x kg nước ở nhiệt độ 15⁰C thu vào để nóng lên

   Q₂ = x.4190.(35 - 15)

Vì nhiệt lượng thu vào bằng nhiệt lượng toả ra nên:

          x.4190.(35 - 15) = y.4190.(100 - 35)      (2)

Giải hệ phương trình (1) và (2) ta được:

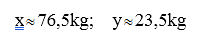
Vậy phải đổ 23,5 lít nước đang sôi vào 76,5 lít nước ở 15⁰C.

V/ Các bài toán về sự trao đổi nhiệt qua thanh và qua các vách ngăn

Sự trao đổi nhiệt qua thanh sẽ có một phần nhiệt lượng hao phí trên thanh dẫn nhiệt. Nhiệt lượng này tỷ lệ với diện tích tiếp xúc của thanh với môi trường, tỷ lệ với độ chênh lệch nhiệt độ của thanh dẫn với nhiệt độ môi trường và phụ thuộc vào chất liệu làm thanh dẫn.

Khi hai thanh dẫn khác nhau được mắc nối tiếp thì năng lượng có ích truyền trên hai thanh là như nhau.

Khi hai thanh dẫn khác nhau mắc song song thì tổng nhiệt lượng có ích truyền trên hai thanh đúng bằng nhiệt lượng có ích của hệ thống.

Khi truyền nhiệt qua các vách ngăn. Nhiệt lượng trao đổi giữa các chất qua vách ngăn tỷ lệ với diện tích các chất tiếp xúc với các vách ngăn và tỷ lệ với độ chênh lệch nhiệt độ giữa hai bên vách ngăn.

Bài 1: Trong một bình cách nhiệt chứa hỗn hợp nước và nước đá ở 0⁰c. Qua thành bên của bình người ta đưa vào một thanh đồng có một lớp cách nhiệt bao quanh. Một đầu của thanh tiếp xúc với nước đá, đầu kia được nhúng trong nước sôi ở áp suất khí quyển. Sau thời gian T_d = 15 phút thì nước đá ở trong bình tan hết. Nếu thay thanh đồng bằng thanh thép có cùng tiết diện nhưng khác nhau về chiều dài với thanh đồng thì nước đá tan hết sau T_t = 48 phút. Cho hai thanh đó nối tiếp với nhau thì nhiệt độ t tại điểm tiếp xúc giữa hai thanh là bao nhiêu? Xét hai trường hợp:

1/ Đầu thanh đồng tiếp xúc với nước sôi

2/ Đầu thanh thép tiếp xúc với nước sôi.

Khi hai thanh nối tiếp với nhau thì sau bao lâu nước đá trong bình tan hết? (giải cho từng trường hợp ở trên)

Giải: Với chiều dài và tiết diện của thanh là xác định thì nhiệt lượng truyền qua thanh dẫn nhiệt trong một đơn vị thời gian chỉ phụ thuộc vào vật liệu làm thanh và hiệu nhiệt độ giữa hai đầu thanh. Lượng nhiệt truyền từ nước sôi sang nước đá để nước đá tan hết qua thanh đồng và qua thanh thép là như nhau. Gọi hệ số tỷ lệ truyền nhiệt đối với các thanh đồng và thép tương ứng là K_d và K_t.

Ta có phương trình:  Q = K_d(t₂ - t₁)T_d = K_t(t₂-t₁)T_t

 Với t₂ = 100 và t₁ = 0 Nên:  $\frac{{{K}_{d}}}{{{K}_{t}}}=\frac{{{T}_{t}}}{{{T}_{d}}}$   = 3,2 

Khi mắc nối tiếp hai thanh thì nhiệt lượng truyền qua các thanh trong 1 s là như nhau. Gọi nhiệt độ ở điểm tiếp xúc giữa hai thanh là t

Trường hợp 1: K_d(t₂-t) = K_t(t - t₁)  Giải phương trình này ta tìm được t = 76⁰c

Trường hợp 2: Tương tự như trường hợp 1. ta tìm được t = 23,8⁰c.

Gọi thời gian để nước đá tan hết  khi mắc nối tiếp hai thanh là T

Với trường hợp 1: Q = K_d(t₂-t₁)T_d = K_d(t₂-t)T = 63 phút.

Tương tự với trường hợp 2 ta cũng có kết quả như trên

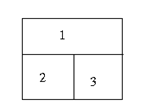
Bài 2:Trong một bình có tiết diện thẳng là hình vuông được  chia làm ba ngăn như hình vẽ. hai ngăn nhỏ có tiết diện thẳng cũng  là hình vuông có cạnh bằng nửa cạnh của bình. Đổ vào các

ngăn đến  cùng một độ  cao ba chất lỏng: Ngăn 1 là nước ở nhiệt độ t₁ = 65⁰c. Ngăn 2 là cà phê ở nhiệt độ t₂ = 35⁰c. Ngăn 3 là sữa ở nhiệt độ t₃ = 20⁰c.  Biết rằng thành bình cách nhiệt rất tốt nhưng vách ngăn có thể dẫn nhiệt.  Nhiệt lượng truyền qua vách ngăn trong một đơn vị thời gian tỷ lệ với diện tích tiếp xúc của chất lỏng và với hiệu nhiệt độ hai bên vách ngăn. Sau một thời gian thì nhiệt độ ngăn chứa nước giảm ∆t₁ = 1⁰c. Hỏi ở hai ngăn còn lại nhiệt độ biến đổi bao nhiêu trong thời gian nói trên? Coi rằng về phương diện nhiệt thì 3 chất nói trên là giống nhau. Bỏ qua sự trao đổi nhiệt của bình và môi trường.

Giải: Vì diện tích tiếp xúc của từng cặp chất lỏng là như nhau. Vậy nhiệt lượng truyền giữa chúng tỷ lệ với hiệu nhiệt độ với cùng một hệ số tỷ lệ K

Tại các vách ngăn. Nhiệt lượng tỏa ra:

Q₁₂ = K(t₁ - t₂);  Q₁₃ = k(t₁ - t₃); Q₂₃ = k(t₂ - t₃)  Từ đó ta có các phương trình cân bằng nhiệt:

Đối với nước: Q₁₂ + Q₂₃ = K(t₁ - t₂ + t₁ -t₃) = 2mc∆t₁

Đối với cà phê: Q₁₂ -Q₂₃ = k(t₁ - t₂ - t₂ + t₃ ) = mc∆t₂

Đối với sữa: Q₁₃ + Q₂₃ = k(t₁ - t₃ + t₂ - t₃) = mc∆t₃

Từ các phương trình trên ta tìm được:  ∆t₂  = 0,4⁰c và ∆t₃ = 1,6⁰c

VI/  Các bài toán liên quan đến công suất tỏa nhiệt của nhiên liệu:

Bài 1:

   Một bếp dầu hoả có hiệu suất 30%.

     a)Tính nhiệt lượng toàn phần mà bếp toả ra khi đốt cháy hoàn toàn 30g dầu hoả?

     b)Với lượng dầu hoả nói trên có thể đun được bao nhiêu lít nước từ 30⁰C đến 100⁰C. Biết năng suất toả nhiệt của dầu hoả là 44.10⁶J/kg , nhiệt dung riêng của nước là 4200J/kg.K.

Giải:

a)      Q_TP =mq = 0,03 .44 10⁶ = 1320 000(J)                                                              

 b)       + Gọi M là khối lượng nước cần đun, theo bài ra ta có:

                                  Q_thu= cMDt = 4200.M.(100 - 30) = 294 000.M(J)       

    +  Từ công thức :       

                                

       

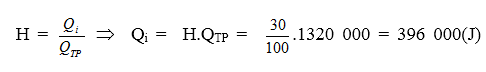
+  Nhiệt lượng cần đun sôi lượng nước là Q_i , theo phương trình cân bằng nhiệt ta có:

                                                                          

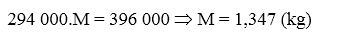
  Vậy với lượng dầu trên đun bằng bếp ta có thể đun được 1,347 kg (1,347l)   nước từ 30⁰C đến 100⁰C.               

VII/ Bài toán đồ thị:

Bài toán: Hai lít nước  được đun trong một chiếc bình đun nước có công suất 500W. Một phần nhiệt tỏa ra môi trường xung quanh.  Sự phụ thuộc của công suất tỏa ra môi trường theo thời gian đun được biểu diễn trên đồ thị như hình vẽ. Nhiệt độ ban đầu của  nước là 20⁰c. Sau bao lâu thì nước trong bình có nhiệt độ là 30⁰c.

Cho nhiệt dung riêng của nước là c = 4200J/kg.K

  

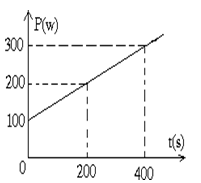
Giải: Gọi đồ thị biểu diễn công suất tỏa ra môi trường là P = a + bt.

               + Khi t = 0 thì P = 100

               + Khi t = 200 thì P = 200

                + Khi t = 400 thì p = 300

     Từ đó ta tìm được P = 100 + 0,5t

Gọi thời gian để nước tăng nhiệt độ từ 20⁰c đến 30⁰c là T thì nhiệt lượng trung bình tỏa ra  trong thời gian này là: P_tb = $\frac{100+100+0,5T}{2}=\frac{200+0,5T}{2}=100+0,25T$ 

Ta có phương trình cân bằng nhiệt: 500T = 2.4200(30 - 20) + (100+0,25T)T

Phương trình có nghiệm: T = 249 s và T = 1351 s

Ta chọn thời gian nhỏ hơn là T = 249s

Bài viết gợi ý: