I. Lý thuyết
*
Điều kiện cộng hưởng
${{\text{Z}}_{\text{L}}}$
= ${{\text{Z}}_{\text{C}}}$ $\Leftrightarrow $ $\text{ }\!\!\omega\!\!\text{
L}$ = $\frac{\text{1}}{\text{ }\!\!\omega\!\!\text{ C}}$ $\Leftrightarrow $ $\text{
}\!\!\omega\!\!\text{ }$ = $\frac{\text{1}}{\sqrt{\text{LC}}}$
*
Hệ quả:
1)
${{\text{I}}_{\text{max}}}$ = $\frac{\text{U}}{\text{R}}$ $\Rightarrow
$ ${{\text{P}}_{\text{ch}}}$ = $\text{I}_{\text{max}}^{\text{2}}\text{R}$ = $\frac{{{\text{U}}^{\text{2}}}}{\text{R}}$
2)
$\text{tan }\!\!\varphi\!\!\text{ }$ = 0 $\Rightarrow $ $\text{
}\!\!\varphi\!\!\text{ }$ = 0 nên u = ${{\text{u}}_{\text{R}}}$, I cùng pha
$\Rightarrow
$ $\overrightarrow{{{\text{U}}_{\text{L}}}}$ $\bot $ $\overrightarrow{\text{U}}$
; $\overrightarrow{{{\text{U}}_{\text{C}}}}$ $\bot $ $\overrightarrow{\text{U}}$
II. Ví dụ minh họa
Ví
dụ 1: Cho đoạn mạch RLC nối tiếp có giá trị các phần tử
cố định. Đặt vào hai đầu đoạn mạch một hiệu điện thế xoay chiều có tần số thay
đổi. Khi tần số góc của dòng điện bằng ${{\text{ }\!\!\omega\!\!\text{
}}_{\text{0}}}$ thì cảm kháng và dung kháng có giá trị 20 $\Omega $ và 80 $\Omega
$. Để trong mạch xảy ra cộng hưởng phải thay đổi tần số góc của dòng điện đến
giá trị bằng bao nhiêu lần ${{\text{ }\!\!\omega\!\!\text{ }}_{0}}$?
Hướng dẫn
${{\text{Z}}_{\text{L}}}$ = ${{\text{
}\!\!\omega\!\!\text{ }}_{\text{0}}}\text{L}$ =20 ($\Omega $) $\Rightarrow $ L
= $\frac{\text{20}}{{{\text{ }\!\!\omega\!\!\text{ }}_{\text{0}}}}$
${{\text{Z}}_{\text{C}}}$ = $\frac{\text{1}}{{{\text{
}\!\!\omega\!\!\text{ }}_{\text{0}}}\text{C}}$ = 80 ($\Omega $) $\Rightarrow $
C = $\frac{\text{1}}{\text{80}{{\text{ }\!\!\omega\!\!\text{ }}_{\text{0}}}}$
Để trong mạch xảy ra cộng hưởng:
$\text{ }\!\!\omega\!\!\text{ }$ = $\frac{\text{1}}{\sqrt{\text{LC}}}$ = $\frac{\text{1}}{\sqrt{\frac{\text{20}}{{{\text{ }\!\!\omega\!\!\text{ }}_{\text{0}}}}\text{.}\frac{\text{1}}{\text{80}{{\text{ }\!\!\omega\!\!\text{ }}_{\text{0}}}}}}$ = $\text{2}{{\text{ }\!\!\omega\!\!\text{ }}_{\text{0}}}$
Ví
dụ 2: Một cuộn dây có điện trở thuần 100 $\Omega $ và
có độ tự cảm $\text{1/ }\!\!\pi\!\!\text{ }$ H nối tiếp với tụ điện có điện
dung $\text{500/ }\!\!\pi\!\!\text{ }$ $\text{ }\!\!\mu\!\!\text{ F}$. Đặt vào
hai đầu đoạn mạch một điệp áp xoay chiều tần số 50 Hz, Để dòng điện trong mạch
cùng pha với điện áp ta phải ghép nối tiếp với tụ C một tụ ${{\text{C}}_{\text{1}}}$
có điện dung là bao nhiêu?
Hướng dẫn
Để $\text{ }\!\!\varphi\!\!\text{ =0}$thì ${{\text{Z}}_{\text{C}}}$
+ ${{\text{Z}}_{\text{C1}}}$ = ${{\text{Z}}_{\text{L}}}$ $\Leftrightarrow $ $\frac{\text{1}}{\text{
}\!\!\omega\!\!\text{ C}}$ + $\frac{\text{1}}{\text{ }\!\!\omega\!\!\text{
}{{\text{C}}_{\text{1}}}}$ = $\text{ }\!\!\omega\!\!\text{ L}$ $\Rightarrow $ ${{\text{C}}_{\text{1}}}$
= $\frac{\text{125}}{\text{ }\!\!\pi\!\!\text{ }}$ ($\text{ }\!\!\mu\!\!\text{
F}$)
Ví
dụ 3: Đoạn mạch xoay chiều RLC mắc nối tiếp, điện trở
thuần của mạch R = 50 $\Omega $. Khi xảy ra cộng hưởng ở tần số ${{\text{f}}_{\text{1}}}$
thì cường độ dòng điện bằng 1 A. Chỉ tăng tần số của mạch điện lên gấp đôi thì
cường độ hiệu dụng trong mạch là 0,8 A. Cảm kháng của cuộn dây khi ở tần số ${{\text{f}}_{\text{1}}}$
bằng bao nhiêu?
Hướng dẫn
Khi f = ${{\text{f}}_{\text{1}}}$ thì ${{\text{Z}}_{\text{C1}}}$
= ${{\text{Z}}_{\text{L1}}}$ và U = ${{\text{U}}_{\text{R}}}$ = ${{\text{I}}_{\text{1}}}\text{R}$
= 50 (V)
Khi f = $\text{2}{{\text{f}}_{\text{1}}}$ thì ${{\text{Z}}_{\text{L2}}}$
= $\text{2}{{\text{Z}}_{\text{L1}}}$, ${{\text{Z}}_{\text{C2}}}$
= ${{\text{Z}}_{\text{C1}}}\text{/2}$ = ${{\text{Z}}_{\text{L1}}}/2$
${{\text{Z}}_{\text{2}}}$ = $\sqrt{{{\text{R}}^{\text{2}}}\text{+}{{\left(
{{\text{Z}}_{\text{L2}}}\text{-}{{\text{Z}}_{\text{C2}}} \right)}^{\text{2}}}}$
= $\frac{\text{U}}{{{\text{I}}_{\text{2}}}}$ $\Leftrightarrow $ $\sqrt{\text{5}{{\text{0}}^{\text{2}}}\text{+2}\text{.25}\text{.Z}_{\text{L1}}^{\text{2}}}$
= $\frac{50}{0,8}$ $\Rightarrow $ ${{\text{Z}}_{\text{L1}}}$ = 25 ($\Omega $)
Ví dụ 4: Một đoạn mạch AB gồm 2 đoạn AM và MB mắc nối tiếp. Đoạn mạch AM gồm điện trở thuần ${{\text{R}}_{\text{1}}}$ mắc nối tiếp với tụ điện có điện dung C, đoạn mạch MB gồm điện trở thuần ${{\text{R}}_{\text{2}}}$ mắc nối tiếp với cuộn cảm thuần có độ tự cảm L. Đặt điệp áp xoay chiều u = ${{\text{U}}_{\text{0}}}\text{cos }\!\!\omega\!\!\text{ t}$ (${{\text{U}}_{\text{0}}}$ và $\text{ }\!\!\omega\!\!\text{ }$ không đổi) vào hai đầu đoạn mạch AB thì công suất tiêu thụ của đoạn mạch AB là 85 W. Khi đó $\text{LC}{{\text{ }\!\!\omega\!\!\text{ }}^{\text{2}}}$ = 1 và độ lệch pha giữa ${{\text{u}}_{\text{AM}}}$ và ${{\text{u}}_{\text{MB}}}$ là ${{90}^{0}}$. Nếu đặt điện áp trên vào hai đầu đoạn mạch MB thì đoạn mạch này tiêu thụ công suất bẳng bao nhiêu?

Hướng dẫn
* Đặt điện áp vào hai đầu đoạn AB:
${{\text{Z}}_{\text{L}}}$ = ${{\text{Z}}_{\text{C}}}$
$\Rightarrow $ P = $\frac{{{\text{U}}^{\text{2}}}}{{{\text{R}}_{\text{1}}}\text{+}{{\text{R}}_{\text{2}}}}$
$\text{tan}{{\text{ }\!\!\varphi\!\!\text{
}}_{\text{AM}}}$.$\text{tan}{{\text{ }\!\!\varphi\!\!\text{ }}_{\text{MB}}}$ =
-1 $\Rightarrow $ $\frac{\text{-}{{\text{Z}}_{\text{C}}}}{{{\text{R}}_{\text{1}}}}$.$\frac{{{\text{Z}}_{\text{L}}}}{{{\text{R}}_{\text{2}}}}$
= -1 $\Rightarrow $ $\text{Z}_{\text{L}}^{\text{2}}$ = ${{\text{R}}_{\text{1}}}{{\text{R}}_{\text{2}}}$
* Đặt điện áp vào MB
P’ = ${{\text{I}}^{\text{ }\!\!'\!\!\text{
2}}}{{\text{R}}_{\text{2}}}$ = $\frac{{{\text{U}}^{\text{2}}}{{\text{R}}_{\text{2}}}}{\text{R}_{\text{2}}^{\text{2}}\text{+Z}_{\text{L}}^{\text{2}}}$
=$\frac{{{\text{U}}^{\text{2}}}{{\text{R}}_{\text{2}}}}{\text{R}_{\text{2}}^{\text{2}}\text{+}{{\text{R}}_{\text{1}}}{{\text{R}}_{\text{2}}}}$
= $\frac{{{\text{U}}^{\text{2}}}}{{{\text{R}}_{\text{1}}}\text{+}{{\text{R}}_{\text{2}}}}$
= P = 85 (W)
Ví
dụ 5: Một đoạn mạch xoay chiều nối tiếp AB gồm điện trở
thuần R, cuộn cảm thuần L và tụ điện có điện dung C. Điện áp hai đầu đoạn mạch
AB là u = ${{\text{U}}_{\text{0}}}\text{cos }\!\!\omega\!\!\text{ t}$ V thì điện
áp trên L là ${{\text{u}}_{\text{L}}}$ = ${{\text{U}}_{\text{0}}}\sqrt{\text{2}}$cos($\text{
}\!\!\omega\!\!\text{ t}$ + $\text{ }\!\!\pi\!\!\text{ /4}$) V. Muốn mạch xảy
ra cộng hưởng điện dung của tụ bằng bao nhiêu?
Hướng dẫn
Vì i luôn trễ pha hơn ${{\text{u}}_{\text{L}}}$ là
$\text{ }\!\!\pi\!\!\text{ /2}$ và u trễ pha hơn ${{\text{u}}_{\text{L}}}$ là $\text{
}\!\!\pi\!\!\text{ /4}$ nên $\text{ }\!\!\varphi\!\!\text{ }$ = $\text{
}\!\!\pi\!\!\text{ /4}$
$\text{tan }\!\!\varphi\!\!\text{ }$ = $\frac{{{\text{Z}}_{\text{L}}}\text{-}{{\text{Z}}_{\text{C}}}}{\text{R}}$
= $\text{tan}\frac{\text{ }\!\!\pi\!\!\text{ }}{\text{4}}$ $\Rightarrow $ R = ${{\text{Z}}_{\text{L}}}\text{-}{{\text{Z}}_{\text{C}}}$
> 0
${{\text{U}}_{\text{L}}}$ = $\text{2}\sqrt{\text{2}}{{\text{U}}_{\text{AB}}}$
$\Rightarrow $ ${{\text{Z}}_{\text{L}}}$ = $2\sqrt{2}\sqrt{{{\text{R}}^{\text{2}}}\text{+}{{\left(
{{\text{Z}}_{\text{L}}}\text{-}{{\text{Z}}_{\text{C}}} \right)}^{2}}}$
$\Rightarrow $ ${{\text{Z}}_{\text{L}}}$ = 4(${{\text{Z}}_{\text{L}}}$
- ${{\text{Z}}_{\text{C}}}$) $\Rightarrow $ ${{\text{Z}}_{\text{L}}}$ = \[\frac{\text{4}}{\text{3}}{{\text{Z}}_{\text{C}}}\]
Để mạch xảy ra cộng hưởng thì
$\text{Z}_{\text{C}}^{\text{ }\!\!'\!\!\text{ }}$ =
${{\text{Z}}_{\text{L}}}$ $\Leftrightarrow $ $\text{Z}_{\text{C}}^{\text{
}\!\!'\!\!\text{ }}$ = \[\frac{\text{4}}{\text{3}}{{\text{Z}}_{\text{C}}}\] $\Leftrightarrow
$ $\frac{\text{1}}{\text{ }\!\!\omega\!\!\text{ C }\!\!'\!\!\text{ }}$ = $\frac{\text{4}}{\text{3}}\frac{\text{1}}{\text{
}\!\!\omega\!\!\text{ C}}$ $\Leftrightarrow $ C’ = $\frac{\text{3}}{\text{4}}\text{C}$
Ví
dụ 6: Một đoạn mạch nối tiếp gồm cuộn cảm thuần, tụ điện
và điện trở R. Đặt vào hai đầu đoạn mạch điện áp xoay chiều có giá trị hiệu dụng
U thì dung kháng gấp bốn lần ảm kháng. Nếu chỉ tăng tần số dòng điện k lần thì
điện áp hiệu dụng hai đầu điện trở R là U. Tìm giá trị k.
Hướng dẫn
${{\text{Z}}_{\text{C}}}$ = $\text{4}{{\text{Z}}_{\text{L}}}$
$\Rightarrow $ $\text{ }\!\!\omega\!\!\text{ L}$ = $\frac{\text{4}}{\text{
}\!\!\omega\!\!\text{ C}}$ $\Leftrightarrow $
LC = $\frac{\text{1}}{\text{4}{{\text{ }\!\!\omega\!\!\text{
}}^{\text{2}}}}$ (1)
${{\text{U}}_{\text{R}}}$ = U (mạch cộng hưởng) $\Rightarrow
$ ${{\text{ }\!\!\omega\!\!\text{ }}_{0}}\text{L}$ = $\frac{\text{1}}{{{\text{
}\!\!\omega\!\!\text{ }}_{0}}\text{C}}$ $\Leftrightarrow $ LC = $\frac{\text{1}}{\text{
}\!\!\omega\!\!\text{ }_{0}^{2}}$ (2)
Từ (1), (2) suy ra $\frac{\text{1}}{\text{
}\!\!\omega\!\!\text{ }_{0}^{2}}$ = $\frac{\text{1}}{\text{4}{{\text{
}\!\!\omega\!\!\text{ }}^{\text{2}}}}$ $\Rightarrow $ \[{{\text{
}\!\!\omega\!\!\text{ }}_{0}}\] = $\text{2 }\!\!\omega\!\!\text{ }$
Ví
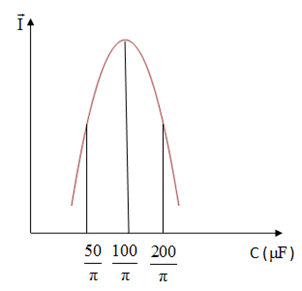
dụ 7: Đặt điệp áp xoay chiều u = 220$\text{cos100
}\!\!\pi\!\!\text{ t}$ (V) vào hai đầu đoạn mạch gồm điện trở thuần 100 $\Omega
$. Cuộn dây thuần cảm có độ tự cảm $\text{1/ }\!\!\pi\!\!\text{ }$ H và tụ điện
có điện dung C thay đổi mắc nối tiếp. Nếu thay đổi điện dung C từ $\text{200/
}\!\!\pi\!\!\text{ }$ $\text{ }\!\!\mu\!\!\text{ F}$ đến $\text{50/
}\!\!\pi\!\!\text{ }$ $\text{ }\!\!\mu\!\!\text{ F}$ thì cường độ dòng điện hiệu
dụng qua mạch bằng bao nhiêu?
Hướng dẫn
Khi mạch cộng hưởng: ${{\text{Z}}_{\text{L}}}$ = ${{\text{Z}}_{\text{C}}}$
$\Leftrightarrow $ ${{\text{C}}_{\text{0}}}$ = $\frac{\text{1}}{\text{L}{{\text{
}\!\!\omega\!\!\text{ }}^{\text{2}}}}$ = $\frac{\text{100}}{\text{
}\!\!\pi\!\!\text{ }}$ ($\text{ }\!\!\mu\!\!\text{ F}$)
Vì $\frac{\text{200}}{\text{ }\!\!\pi\!\!\text{
}}$ ($\text{ }\!\!\mu\!\!\text{ F}$)
> ${{\text{C}}_{\text{0}}}$ > $\frac{\text{50}}{\text{
}\!\!\pi\!\!\text{ }}$ ($\text{ }\!\!\mu\!\!\text{ F}$) nên I tăng rồi giảm
Ví
dụ 8: Hai đoạn mạch nối tiếp RLC khác nhau: mạch 1 và mạch
2. Cộng hưởng với dòng điện xoay chiều có tần số góc lần lượt là ${{\text{
}\!\!\omega\!\!\text{ }}_{\text{0}}}$ và $\text{2}{{\text{
}\!\!\omega\!\!\text{ }}_{\text{0}}}$. Biết độ tự cảm của mạch 2 gấp ba lần độ
tự cảm của mạch 1. Mắc nối tiếp hai đoạn mạch đó với nhau thành một mạch thì nó
sẽ cộng hưởng với dòng điện xoay chiều có tần số góc là bao nhiêu?
Hướng dẫn
$\text{ }\!\!\omega\!\!\text{
}_{\text{1}}^{\text{2}}{{\text{L}}_{\text{1}}}{{\text{C}}_{\text{1}}}$ = 1 $\Rightarrow
$ $\frac{\text{1}}{{{\text{C}}_{\text{1}}}}$ = $\text{ }\!\!\omega\!\!\text{
}_{\text{1}}^{\text{2}}{{\text{L}}_{\text{1}}}$
$\text{ }\!\!\omega\!\!\text{
}_{2}^{\text{2}}{{\text{L}}_{2}}{{\text{C}}_{2}}$ = 1 $\Rightarrow $ $\frac{\text{1}}{{{\text{C}}_{2}}}$
= $\text{ }\!\!\omega\!\!\text{ }_{2}^{\text{2}}{{\text{L}}_{2}}$
$\text{ }\!\!\omega\!\!\text{
}{{\text{L}}_{\text{1}}}$ + $\text{ }\!\!\omega\!\!\text{
}{{\text{L}}_{\text{2}}}$ = $\frac{\text{1}}{\text{ }\!\!\omega\!\!\text{
}{{\text{C}}_{\text{1}}}}$ + $\frac{\text{1}}{\text{ }\!\!\omega\!\!\text{
}{{\text{C}}_{\text{2}}}}$
$\Rightarrow $ ${{\text{ }\!\!\omega\!\!\text{
}}^{\text{2}}}\left( {{\text{L}}_{\text{1}}}\text{+}{{\text{L}}_{\text{2}}}
\right)$ = $\text{ }\!\!\omega\!\!\text{
}_{\text{1}}^{\text{2}}{{\text{L}}_{\text{1}}}$ + $\text{ }\!\!\omega\!\!\text{
}_{\text{2}}^{\text{2}}{{\text{L}}_{\text{2}}}$
$\Leftrightarrow $ ${{\text{ }\!\!\omega\!\!\text{
}}^{\text{2}}}$.$\text{4}{{\text{L}}_{\text{1}}}$ = $\text{
}\!\!\omega\!\!\text{ }_{\text{0}}^{\text{2}}{{\text{L}}_{\text{1}}}$ + $\text{4
}\!\!\omega\!\!\text{ }_{\text{0}}^{\text{2}}$.$\text{3}{{\text{L}}_{\text{1}}}$
$\Rightarrow $ $\text{ }\!\!\omega\!\!\text{ }$ = $\text{0,5}\sqrt{\text{13}}{{\text{
}\!\!\omega\!\!\text{ }}_{\text{0}}}$
Ví
dụ 9: Mạch xoay chiều ${{\text{R}}_{\text{1}}}$, ${{\text{L}}_{\text{1}}}$,
${{\text{C}}_{\text{1}}}$ mắc nối tiếp có tần số cộng hưởng ${{\text{f}}_{\text{1}}}$.
Mạch xoay chiều ${{\text{R}}_{2}}$, ${{\text{L}}_{2}}$, ${{\text{C}}_{2}}$ mắc
nối tiếp có tần số cộng hưởng ${{\text{f}}_{2}}$. Biết ${{\text{C}}_{\text{1}}}$
= $\text{2}{{\text{C}}_{\text{2}}}$ và ${{\text{f}}_{\text{2}}}$ =$\text{2}{{\text{f}}_{\text{1}}}$.
Mắc nối tiếp hai mạch đó với nhau thì tần số cộng hưởng là bao nhiêu?
Hướng dẫn
$\text{ }\!\!\omega\!\!\text{
}_{\text{1}}^{\text{2}}{{\text{L}}_{\text{1}}}{{\text{C}}_{\text{1}}}$ = 1 $\Rightarrow
$ ${{\text{L}}_{\text{1}}}$ = $\frac{\text{1}}{\text{ }\!\!\omega\!\!\text{
}_{\text{1}}^{\text{2}}{{\text{C}}_{\text{1}}}}$
$\text{ }\!\!\omega\!\!\text{
}_{\text{2}}^{\text{2}}{{\text{L}}_{\text{2}}}{{\text{C}}_{\text{2}}}$ = 1 $\Rightarrow
$ ${{\text{L}}_{\text{2}}}$ = $\frac{\text{1}}{\text{ }\!\!\omega\!\!\text{
}_{\text{2}}^{\text{2}}{{\text{C}}_{\text{2}}}}$ = $\frac{\text{1}}{\text{
}\!\!\omega\!\!\text{ }_{\text{1}}^{\text{2}}{{\text{C}}_{\text{1}}}}$
Mạch xảy ra cộng hưởng
$\Leftrightarrow $ $\text{ }\!\!\omega\!\!\text{
}{{\text{L}}_{\text{1}}}$ + $\text{ }\!\!\omega\!\!\text{
}{{\text{L}}_{\text{2}}}$ = $\frac{\text{1}}{\text{ }\!\!\omega\!\!\text{
}{{\text{C}}_{\text{1}}}}$ + $\frac{\text{1}}{\text{ }\!\!\omega\!\!\text{
}{{\text{C}}_{\text{2}}}}$
$\Rightarrow $ ${{\text{ }\!\!\omega\!\!\text{
}}^{\text{2}}}$\[\left( \frac{\text{1}}{\text{ }\!\!\omega\!\!\text{
}_{\text{1}}^{\text{2}}{{\text{C}}_{\text{1}}}}+\frac{\text{1}}{\text{2
}\!\!\omega\!\!\text{ }_{\text{1}}^{\text{2}}{{\text{C}}_{\text{1}}}} \right)\]
= $\frac{\text{1}}{{{\text{C}}_{\text{1}}}}$ + $\frac{\text{2}}{{{\text{C}}_{\text{1}}}}$
$\Rightarrow $ $\text{ }\!\!\omega\!\!\text{ }$ = ${{\text{
}\!\!\omega\!\!\text{ }}_{\text{1}}}\sqrt{\text{2}}$
III. Bài tập tự luyện
Bài 1: Một đoạn mạch
xoay chiều tần số 50 Hz nối tiếp RLC, điện dung của tụ $\text{50/
}\!\!\pi\!\!\text{ }$ $\text{ }\!\!\mu\!\!\text{ F}$. Nếu điện áp trên C lệch
pha $\text{ }\!\!\pi\!\!\text{ /2}$ so với điện áp hai đầu đoạn mạch thì cuộn cảm
thuần có độ tự cảm bằng:
A. $\text{0,1/ }\!\!\pi\!\!\text{ }$
H B. $\text{2/
}\!\!\pi\!\!\text{ }$ H B. $\text{0,2/ }\!\!\pi\!\!\text{ }$ H D. $\text{1/
}\!\!\pi\!\!\text{ }$ H
Bài 2: Đoạn mạch
xoay chiều RLC mắc nối tiếp tần số 50 Hz. Điện trở thuần R = 10 $\Omega $, cuộn
dây thuần cảm có độ tự cảm L = $\text{0,1/ }\!\!\pi\!\!\text{ }$ H, tụ điện có
điện dung C. Nếu điện áp hai đầu đoạn mạch cùng pha với điện áp hai đầu điện trở
R thì giá trị điện dung của tụ điện là
A. 3,18 $\text{ }\!\!\mu\!\!\text{
F}$ B. $\text{50/
}\!\!\pi\!\!\text{ }$ $\text{ }\!\!\mu\!\!\text{ F}$ C. $\text{1/
}\!\!\pi\!\!\text{ }$ mF D. $\text{0,1/ }\!\!\pi\!\!\text{ }$ mF
Bài 3: Mạch xoay chiều
RLC nối tiếp. Trường hợp nào sau đầy điện áp hai đầu đoạn mạch cùng pha với điện
áp hai đầu điện trở R
A. Thay đổi C để ${{\text{U}}_{\text{Rmax}}}$ B. Thay đổi
R để ${{\text{U}}_{\text{Cmax}}}$
C. Thay đổi L để ${{\text{U}}_{\text{Lmax}}}$
D. Thay đổi
f để ${{\text{U}}_{\text{Cmax}}}$
Bài 4: Đặt vào hai đầu
một đoạn mạch xoay chiều RLC không phân nhánh điện áp u = ${{\text{U}}_{\text{0}}}\text{cos100
}\!\!\pi\!\!\text{ t}$ V thì hiệu điện thế hai đầu mạch lệch pha $\text{
}\!\!\pi\!\!\text{ /3}$ so với cường độ dòng điện. Biết cuộn cảm thuần có cảm
kháng 20 $\Omega $ còn tụ điện có điện dung thay đổi được. Cho điện dung C tăng
lên hai lần so với giá trị ban đầu thì trong mạch có cộng hưởng điện. Điện trở
thuần của mạch có giá trị bằng
A. $20/\sqrt{3}$ $\Omega
$ B. $20\sqrt{3}$
$\Omega $ C. $10\sqrt{3}$
$\Omega $ D. $5\sqrt{3}$ $\Omega $
Bài 5: Một đoạn mạch
AB gồm hai đoạn mạch AM và MB mắc nối tiếp. Đoạn mạch AM gồm điện trở thuần ${{\text{R}}_{\text{1}}}$
mắc nối tiếp với tụ điện có điện dung C, đoạn mạch MB gồm điện trở thuần ${{\text{R}}_{\text{2}}}$
mắc nối tiếp với cuộn cảm thuần có độ tự cảm L. Đặt điệp áp xoay chiều u = ${{\text{U}}_{\text{0}}}\text{cos
}\!\!\omega\!\!\text{ t}$ (${{\text{U}}_{\text{0}}}$ và $\text{
}\!\!\omega\!\!\text{ }$ không đổi) vào hai đầu đoạn mạch AB thì công suất tiêu
thụ của đoạn mạch AB là 100 W. Khi đó $\text{LC}{{\text{ }\!\!\omega\!\!\text{
}}^{\text{2}}}$ = 1 và độ lệch pha giữa ${{\text{u}}_{\text{AM}}}$ và ${{\text{u}}_{\text{MB}}}$
là $\text{9}{{\text{0}}^{\text{0}}}$. Nếu đặt điện áp trên vào hai đầu đoạn mạch
MB thì đoạn mạch này tiêu thụ công suất bằng
A. 100 W B. 50 W C. 200 W D. 25 W
Bài 6: Một đoạn mạch
xoay chiều nối tiếp AB gồm điện trở thuần R, cuộn cảm thuần L và tụ điện có điện
dung C. Điện áp hai đầu AB là u = $\text{2}{{\text{U}}_{\text{0}}}\text{cos
}\!\!\omega\!\!\text{ t}$ V thì điện áp trên C là ${{\text{u}}_{\text{C}}}$ = ${{\text{U}}_{\text{0}}}$cos($\text{
}\!\!\omega\!\!\text{ t}$ - $\text{2 }\!\!\pi\!\!\text{ /3}$) V. Muốn mạch xảy
ra cộng hưởng thì điện dung của tụ bằng
A. $\text{C}\sqrt{\text{3}}$
B. $\text{C}\sqrt{\text{2}}$
C. 0,5C D. 2C
Bài 7: Một mạch điện
xoay chiều gồm một tụ điện C nối tiếp với một cuộn dây. Đặt vào hai đầu đoạn mạch
một điện áp u = $\text{U}\sqrt{\text{8}}\text{cos }\!\!\omega\!\!\text{ t}$ V
thì điện áp hai đầu tụ điện C là ${{\text{u}}_{\text{C}}}$ = Ucos($\text{
}\!\!\omega\!\!\text{ t}$ - $\text{3 }\!\!\pi\!\!\text{ /4}$) V. Tỷ số dung
kháng và cảm kháng bằng
A. 3/4 B. 1/3 C. 4/3 D. 2
Bài 8: Đặt vào hai đầu
đoạn mạch RLC nối tiếp vào một điệp áp xoay chiều có giá trị hiệu dụng trên các
phần tử R, L, C lần lượt là 30 V, 50 V và 90 V. Khi thay tụ C bởi tụ C’ để mạch
có cộng hưởng thì điện áp hiệu dụng hai đầu điện trở R bằng
A. 50 V B. 45 V C. 60 V D. 40 V
Bài 9: Một đoạn mạch
nối tiếp gồm cuộn cảm thuần,tụ điện và điện trở R. Đặt vào hai đầu đoạn mạch điệp
áp xoay chiều có giá trị hiệu dụng U thì cảm kháng cuộn cảm gấp bốn lần dung
kháng của tụ. Nếu chỉ giảm tần số dòng điện k lần thì điện áp hiệu dụng hai đầu
điện trở R là U. Giá trị k bằng
A. 0,5 B. 2 C. 4 D. 0,25
Bài 10: Một đoạn mạch
AB mắc nối tiếp gồm điện trở thuần R, tụ điện có điện dung C và cuộn cảm thuần
có độ tự cảm L thay đổi được. Đặt vào hai đầu đoạn mạch AB điệp áp xoay chiều
100 V – 50 Hz. Điều chỉnh L = $\text{0,25C}{{\text{R}}^{\text{2}}}$ và điện áp ở
hai đầu cuộn cảm lệch pha so với điện áp
ở hai đầu đoạn mạch AB góc ${{90}^{0}}$. Điện áp hiệu dụng ở hai đầu tụ điện là
A. 40 V B. 30 V C. 50 V D. 20 V
Bài 11: Đoạn
mạch xoay chiều nối tiếp gồm điện trở thuần R, tụ điện C và cuộn cảm Lr. Đặt
vào hai đầu đoạn mạch một điệp áp xoay chiều 120 V – 50 Hz thì điện áp giữa hai
đầu đoạn R-C và điện áp giữa giữa đầu đoạn C-Lr có cùng một giá trị hiệu dụng
90 V và trong mạch đang có cộng hưởng điện. Điện áp hiệu dụng giữa hai đầu cuộn
cảm là
A. $30\sqrt{17}$
V B. $60\sqrt{2}$
V C. $30\sqrt{3}$
V D. 30 V
Bài 12: Đoạn
mạch gồm điện trở thuần, cuộn dây thuần cảm có độ tự cảm $\text{4/ }\!\!\pi\!\!\text{
}$ H và tụ điện có điện dung $\text{0,1/ }\!\!\pi\!\!\text{ }$ mF nối tiếp. Mắc
đoạn mạch vào nguồn điện xoay chiều có điện áp hiệu dụng không đổi, tần số f
thay đổi được. Khi cho f thay đổi từ 20 Hz đến 30 Hz thì cường độ hiệu dụng của
dòng điện trong mạch
A. tăng rồi giảm B. giảm C. tăng D. giảm rồi tăng
Bài 13: Dung kháng của
một đoạn mạch RLC nối tiếp đang có giá trị nhỏ hơn cảm kháng. Thay đổi chỉ một
thong số trong các thong số của đoạn mạch bằng các cách nêu sau, cách nào có thể
làm cho hiện tượng cộng hưởng điện xảy ra?
A. Tăng điện dung của tụ
điện B. Tăng hệ
số tự cảm của cuộn dây
C. Giảm điện trở thuần
của đoạn mạch D. Giảm
tần số dòng điện
Bài 14: Chọn câu sai
trong các câu sau: Mạch điện xoay chiều RLC nối tiếp đang xảy ra cộng hưởng. Nếu
thay đổi tần số của điện áp đặt vào hai đầu đoạn mạch thì
A. Điện áp hiệu dụng
trên L tăng
B. Công suất trung bình
trên đoạn mạch giảm
C. Hệ số công suất của
mạch giảm
D. Cường độ hiệu dụng
qua mạch giảm
Bài 15: Đoạn mạch
xoay chiều tần số f gồm điện trở thuần R, cuộn dây có cảm kháng ${{\text{Z}}_{\text{L}}}$
và tụ điện có dung kháng ${{\text{Z}}_{\text{C}}}$ mắc nối tiếp. Nếu tăng dần tần
số từ giá trị f thì điện áp hiệu dụng trên R tăng rồi giảm.Chọn kết luận đúng.
A. ${{\text{Z}}_{\text{L}}}$
> ${{\text{Z}}_{\text{C}}}$ B. \[{{\text{Z}}_{\text{L}}}\] < ${{\text{Z}}_{\text{C}}}$
C. ${{\text{Z}}_{\text{L}}}$
= ${{\text{Z}}_{\text{C}}}$ D. cuộn dây có điện trở bằng 0
Bài 16: Trong mạch điện
xoay chiều RLC nối tiếp đang có cộng hưởng điện thì kết luận nào sau đây sai?
A. Điện áp hiệu dụng ở
hai đầu cuộn cảm bằng điện áp hiệu dụng hai đầu tụ điện.
B. Cường độ hiệu dụng
trong mạch cực đại.
C. Điện áp hiệu dụng ở
hai đầu đoạn mạch lớn hơn điện áp hiệu dụng ở hai đầu điện trở R.
D. Điện áp hai đầu đoạn
mạch cùng pha với điện áp hai đầu điện trở R.
Bài 17: Hai đoạn mạch
nối tiếp RLC khác nhau: mạch 1 và mạch 2., cộng hưởng với dòng điện xoay chiều
có tần số lần lượt là f và 2f. Biết độ tự cảm của mạch 2 gấp đôi độ tự cảm của
mạch 1. Nếu mắc nối tiếp hai đoạn mạch đó với nhau thành một mạch thì nó xẽ cộng
hưởng với dòng điện xoay chiều có tần số
A. $\text{f}\sqrt{\text{3}}$
B. $\text{3f}$
C. f D. $\text{f}\sqrt{\text{2}}$
Bài 18: Mạch điện X gồm
3 phần tử ${{\text{R}}_{\text{1}}}$, ${{\text{L}}_{\text{1}}}$, ${{\text{C}}_{\text{1}}}$
mắc nối tiếp có tần số góc khi cộng hưởng là ${{\text{ }\!\!\omega\!\!\text{
}}_{\text{1}}}$ và mạch điện Y gồm 3 phần tử ${{\text{R}}_{\text{2}}}$, ${{\text{L}}_{\text{2}}}$,
${{\text{C}}_{\text{2}}}$ mắc nối tiếp có tần số góc khi cộng hưởng là ${{\text{
}\!\!\omega\!\!\text{ }}_{\text{2}}}$. Biết ${{\text{ }\!\!\omega\!\!\text{
}}_{\text{1}}}$ $\ne $ ${{\text{ }\!\!\omega\!\!\text{ }}_{\text{2}}}$ và ${{\text{L}}_{\text{1}}}$
= $\text{2}{{\text{L}}_{\text{2}}}$. Mắc nối tiếp hai mạch X và Y với nhau thì
tần số góc khi cộng hưởng của mạch này là
A. $\sqrt{{{\text{
}\!\!\omega\!\!\text{ }}_{\text{1}}}{{\text{ }\!\!\omega\!\!\text{
}}_{\text{2}}}}$ B. $\sqrt{\frac{\text{2
}\!\!\omega\!\!\text{ }_{\text{1}}^{\text{2}}\text{+ }\!\!\omega\!\!\text{
}_{\text{2}}^{\text{2}}}{\text{3}}}$ C. $\sqrt{\frac{\text{ }\!\!\omega\!\!\text{ }_{\text{1}}^{\text{2}}\text{+2
}\!\!\omega\!\!\text{ }_{\text{2}}^{\text{2}}}{\text{3}}}$ D. $\sqrt{{{\text{
}\!\!\omega\!\!\text{ }}_{\text{1}}}\text{+}{{\text{ }\!\!\omega\!\!\text{
}}_{\text{2}}}}$
Bài 19: Hai đoạn mạch
nối tiếp RLC khác nhau: mạch 1 và mạch 2, cộng hưởng với dòng điện xoay chiều
có tần số góc lần lượt là ${{\text{ }\!\!\omega\!\!\text{ }}_{\text{0}}}$ và ${{\text{
}\!\!\omega\!\!\text{ }}_{\text{0}}}\text{/2}$. Biết điện dung của mạch 2 bằng
một nửa điện dung mạch 1. Nếu mắc nối tiếp hai đoạn mạch đó với nhau thành một
mạch thì nó sẽ cộng hưởng với dòng điện xoay chiều có tần số
A. ${{\text{
}\!\!\omega\!\!\text{ }}_{\text{0}}}\sqrt{\text{3}}$ B. $\text{1,5}{{\text{
}\!\!\omega\!\!\text{ }}_{\text{0}}}$ C. $\text{2}{{\text{ }\!\!\omega\!\!\text{
}}_{\text{0}}}\sqrt{\text{3}}$ D. ${{\text{ }\!\!\omega\!\!\text{
}}_{\text{0}}}\text{/}\sqrt{\text{3}}$
Bài 20: Khi nói về hệ
số công suất $\text{cos }\!\!\varphi\!\!\text{ }$ của đoạn mạch xoay chiều,
phát biểu nào sai?
A. Với đoạn mạch chỉ có
tụ điện hoặc chỉ có cuộn cảm thuần thì $\text{cos }\!\!\varphi\!\!\text{ }$ = 0
B. Với đoạn mạch RLC mắc
nối tiếp đang xảy ra hiện tượng cổng hưởng thì $\text{cos
}\!\!\varphi\!\!\text{ }$ = 0
C. Với đoạn mạch chỉ có
điện trở thuần thì $\text{cos }\!\!\varphi\!\!\text{ }$ = 1
D. Với đoạn mạch gồm tụ
điện và điện trở thuần mắc nối tiếp thì 0 < $\text{cos
}\!\!\varphi\!\!\text{ }$ < 1
Bài 21: Khi có cộng
hưởng điện trong đoạn mạch điện xoay chiều RLC không phân nhánh thì
A. cường độ dòng điện tức
thời trong mạch cùng pha với điện áp tức thời đặt vào hai đầu đoạn mạch.
B. điện áp tức thời giữa
hai đầu điện trở thuần cùng pha với điện áp tức thời giữa hai đầu cuộn cảm.
C. điện áp tức thời giữa
hai đầu điện trở thuần cùng pha với điện áp tức thời giữa hai bản tụ điện.
D. công suất tiêu thụ
trên đoạn mạch đạt giá trị nhỏ nhất
Bài 22: Gọi u, ${{\text{u}}_{\text{R}}}$,
${{\text{u}}_{\text{L}}}$, ${{\text{u}}_{\text{C}}}$ lần lượt là điện áp tức thời
hai đầu đoạn mạch, hai đầu điện trở R, hai đầu cuộn cảm thuần L và hai đầu tụ
điện C của đoạn mạch nối tiếp RLC. Thay đổi tần số dòng điện qua mạch sao cho
trong mạch xảy ra cộng hưởng điện thì
A. u = ${{\text{u}}_{\text{C}}}$
B. u = ${{\text{u}}_{\text{R}}}$
C. ${{\text{u}}_{\text{L}}}$
= ${{\text{u}}_{\text{C}}}$ D. ${{\text{u}}_{\text{R}}}$ = ${{\text{u}}_{\text{L}}}$
* Đáp án
|
1 B |
2 C |
3
A |
4
A |
5
A |
6 B |
7 B |
8
A |
9 B |
10 C |
|
11 B |
12
A |
13 D |
14
A |
15 B |
16 C |
17 A |
18 B |
19 D |
20 B |
|
21 A |
22 B |
|
|
|
|
|
|
|
|







