I.
LÝ THUYẾT
Cho
mạch RLC mắc nối tiếp được đặt vào điệp áp xoay chiều u = $\text{U}\sqrt{\text{2}}$cos\[\text{
}\!\!\omega\!\!\text{ t}\] với U không đổi, $\text{ }\!\!\omega\!\!\text{ }$ có
thể thay đổi.
*
Để P, I, ${{\text{U}}_{\text{R}}}$ max
Ta có: I = $\frac{\text{U}}{\sqrt{{{\text{R}}^{\text{2}}}\text{+}{{\left(
{{\text{Z}}_{\text{L}}}\text{-}{{\text{Z}}_{\text{C}}} \right)}^{\text{2}}}}}$
= $\frac{\text{U}}{\sqrt{{{\text{R}}^{\text{2}}}\text{+}{{\left( \text{
}\!\!\omega\!\!\text{ L-}\frac{\text{1}}{\text{ }\!\!\omega\!\!\text{ C}}
\right)}^{\text{2}}}}}$
P = ${{\text{I}}^{\text{2}}}$R = $\frac{{{\text{U}}^{2}}}{{{\text{R}}^{\text{2}}}\text{+}{{\left(
\text{ }\!\!\omega\!\!\text{ L-}\frac{\text{1}}{\text{ }\!\!\omega\!\!\text{
C}} \right)}^{\text{2}}}}$.R
${{\text{U}}_{\text{R}}}$ = IR = $\frac{\text{U}}{\sqrt{{{\text{R}}^{\text{2}}}\text{+}{{\left(
\text{ }\!\!\omega\!\!\text{ L-}\frac{\text{1}}{\text{ }\!\!\omega\!\!\text{
C}} \right)}^{\text{2}}}}}$R
+ Khi $\text{
}\!\!\omega\!\!\text{ }$ = 0 thì $\frac{\text{1}}{\text{ }\!\!\omega\!\!\text{
C}}$ $\to $ $\infty $ làm cho P = 0
+ Khi $\text{
}\!\!\omega\!\!\text{ }$ = ${{\text{ }\!\!\omega\!\!\text{ }}_{\text{0}}}$ = $\frac{\text{1}}{\sqrt{\text{LC}}}$
thì mạch cộng hưởng làm cho P = ${{\text{P}}_{\text{max}}}$
+ Khi $\text{
}\!\!\omega\!\!\text{ }$ $\to $ $\infty $ thì $\text{ }\!\!\omega\!\!\text{ L}$
$\to $ $\infty $ làm cho P = 0
Ta có:

Đồ thị:
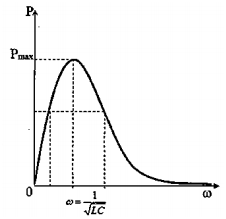
$\mapsto $ Khi $\text{ }\!\!\omega\!\!\text{ }$ thay đổi
thì I, P, ${{\text{U}}_{\text{R}}}$ đạt giá cực đại khi mạch điện xảy ra hiện
tượng cộng hưởng.
${{\text{Z}}_{\text{L}}}$
= ${{\text{Z}}_{\text{C}}}$ $\Leftrightarrow $ $\text{ }\!\!\omega\!\!\text{ }$L
= $\frac{\text{1}}{\text{ }\!\!\omega\!\!\text{ C}}$ $\Rightarrow $ $\text{
}\!\!\omega\!\!\text{ }$ = ${{\text{ }\!\!\omega\!\!\text{ }}_{0}}$ = $\frac{\text{1}}{\sqrt{\text{LC}}}$
${{\text{I}}_{\text{max}}}$
= $\frac{\text{U}}{\text{R}}$ ; ${{\text{P}}_{\text{max}}}$ = $\frac{{{\text{U}}^{\text{2}}}}{\text{R}}$
; ${{\left( {{\text{U}}_{\text{R}}} \right)}_{\text{max}}}$ = U
*
Để ${{\text{U}}_{\text{L}}}$ max
${{\text{U}}_{\text{L}}}$
= I.${{\text{Z}}_{\text{L}}}$ = $\frac{\text{U}\text{.}{{\text{Z}}_{\text{L}}}}{\text{Z}}$
= $\frac{\text{U}\text{.}{{\text{Z}}_{\text{L}}}}{\sqrt{{{\text{R}}^{\text{2}}}\text{+}{{\left(
{{\text{Z}}_{\text{L}}}\text{-}{{\text{Z}}_{\text{C}}} \right)}^{\text{2}}}}}$
= $\frac{\text{U}}{\sqrt{\frac{{{\text{R}}^{\text{2}}}}{\text{Z}_{\text{L}}^{\text{2}}}\text{+}\frac{\text{Z}_{\text{C}}^{\text{2}}}{\text{Z}_{\text{L}}^{\text{2}}}\text{-}\frac{\text{2}{{\text{Z}}_{\text{C}}}}{{{\text{Z}}_{\text{L}}}}+1}}$
= \[\frac{\text{U}}{\sqrt{\frac{\text{1}}{{{\text{L}}^{\text{2}}}{{\text{C}}^{\text{2}}}}\text{.}\frac{\text{1}}{{{\text{
}\!\!\omega\!\!\text{ }}^{\text{4}}}}\text{+}\left( \frac{{{\text{R}}^{\text{2}}}}{{{\text{L}}^{\text{2}}}}\text{-}\frac{\text{2}}{\text{LC}}
\right)\text{.}\frac{\text{1}}{{{\text{ }\!\!\omega\!\!\text{
}}^{\text{2}}}}\text{+1}}}\]
Đặt 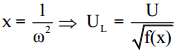 với f(x) = \[\frac{\text{1}}{{{\text{L}}^{\text{2}}}{{\text{C}}^{\text{2}}}}\text{.}{{\text{x}}^{\text{2}}}\text{+}\left(
\frac{{{\text{R}}^{\text{2}}}}{{{\text{L}}^{\text{2}}}}\text{-}\frac{\text{2}}{\text{LC}}
\right)\text{.x+1}\]
với f(x) = \[\frac{\text{1}}{{{\text{L}}^{\text{2}}}{{\text{C}}^{\text{2}}}}\text{.}{{\text{x}}^{\text{2}}}\text{+}\left(
\frac{{{\text{R}}^{\text{2}}}}{{{\text{L}}^{\text{2}}}}\text{-}\frac{\text{2}}{\text{LC}}
\right)\text{.x+1}\]
Để ${{\text{U}}_{\text{L}}}$
max thì f(x) min tại
x = $\frac{\text{1}}{{{\text{
}\!\!\omega\!\!\text{ }}^{\text{2}}}}$ = - $\frac{\text{b}}{\text{2a}}$ = - $\frac{\frac{{{\text{R}}^{\text{2}}}}{{{\text{L}}^{\text{2}}}}\text{-}\frac{\text{2}}{\text{LC}}}{\text{2}\text{.}\frac{\text{1}}{{{\text{L}}^{\text{2}}}{{\text{C}}^{\text{2}}}}}$
= $\frac{\text{2LC-}{{\text{R}}^{\text{2}}}{{\text{C}}^{\text{2}}}}{\text{2}}$
$\Rightarrow
$ $\text{ }\!\!\omega\!\!\text{ }$ = ${{\text{ }\!\!\omega\!\!\text{
}}_{\text{L}}}$ = $\sqrt{\frac{\text{2}}{\text{2LC-}{{\text{R}}^{\text{2}}}{{\text{C}}^{\text{2}}}}}$ $\Rightarrow $ $\text{f}{{\left( \text{x}
\right)}_{\text{min}}}$ = $\frac{\text{4}{{\text{R}}^{\text{2}}}\text{LC-}{{\text{R}}^{\text{4}}}{{\text{C}}^{\text{2}}}}{\text{4}{{\text{L}}^{\text{2}}}}$
$\Rightarrow
$ ${{\left( {{\text{U}}_{\text{L}}} \right)}_{\text{max}}}$ = $\frac{\text{U}}{\sqrt{\text{f(x}{{\text{)}}_{\text{min}}}}}$
= $\frac{\text{U}}{\sqrt{\frac{\text{4}{{\text{R}}^{\text{2}}}\text{LC-}{{\text{R}}^{\text{4}}}{{\text{C}}^{\text{2}}}}{\text{4}{{\text{L}}^{\text{2}}}}}}$
= $\frac{\text{2UL}}{\text{R}\sqrt{\text{4LC-}{{\text{R}}^{\text{2}}}{{\text{C}}^{\text{2}}}}}$
O Phát triển:
$\frac{\text{1}}{\text{
}\!\!\omega\!\!\text{ }_{\text{L}}^{\text{2}}}$ = LC - $\frac{{{\text{R}}^{\text{2}}}{{\text{C}}^{\text{2}}}}{\text{2}}$
$\Rightarrow $ $\frac{\text{1}}{{{\text{ }\!\!\omega\!\!\text{
}}^{\text{2}}}{{\text{C}}^{\text{2}}}}$ = $\frac{\text{L}}{\text{C}}$ - $\frac{{{\text{R}}^{\text{2}}}}{\text{2}}$
$\Leftrightarrow
$ 2$\text{Z}_{\text{C}}^{\text{2}}$ = 2${{\text{Z}}_{\text{L}}}$.${{\text{Z}}_{\text{C}}}$
- ${{\text{R}}^{\text{2}}}$ $\Rightarrow $ ${{\text{R}}^{\text{2}}}$ = 2${{\text{Z}}_{\text{C}}}$(${{\text{Z}}_{\text{L}}}$
- ${{\text{Z}}_{\text{C}}}$)
$\Rightarrow
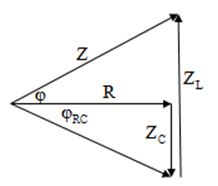
$ $\frac{{{\text{Z}}_{\text{C}}}}{\text{R}}$.$\frac{{{\text{Z}}_{\text{L}}}\text{-}{{\text{Z}}_{\text{C}}}}{\text{R}}$
= $\frac{1}{2}$ $\Leftrightarrow $ tan${{\text{ }\!\!\varphi\!\!\text{ }}_{\text{RC}}}$.tan$\text{
}\!\!\varphi\!\!\text{ }$ = $\frac{1}{2}$
$\mapsto $ ${{\text{U}}_{\text{Lmax}}}$
= $\frac{\text{U}}{\sqrt{\text{1-}\frac{\text{Z}_{\text{C}}^{\text{2}}}{\text{Z}_{\text{L}}^{\text{2}}}}}$
= $\frac{\text{U}}{\sqrt{\text{1-}\left(
\frac{{{\text{U}}_{\text{C}}}}{{{\text{U}}_{\text{Lmax}}}} \right)}}$
$\Rightarrow $ ${{\text{U}}^{\text{2}}}$
= $\text{U}_{\text{Lmax}}^{\text{2}}$ - $\text{U}_{\text{C}}^{\text{2}}$ ; ${{\text{Z}}^{\text{2}}}$
= $\text{Z}_{\text{L}}^{\text{2}}$ - $\text{Z}_{\text{C}}^{\text{2}}$
*
Để ${{\text{U}}_{\text{C}}}$ max
${{\text{U}}_{\text{C}}}$
= I.${{\text{Z}}_{\text{C}}}$ = $\frac{\text{U}\text{.}{{\text{Z}}_{\text{C}}}}{\text{Z}}$
= $\frac{\text{U}\text{.}{{\text{Z}}_{\text{C}}}}{\sqrt{{{\text{R}}^{\text{2}}}\text{+}{{\left(
{{\text{Z}}_{\text{L}}}\text{-}{{\text{Z}}_{\text{C}}} \right)}^{\text{2}}}}}$
= $\frac{\text{U}}{\sqrt{\frac{{{\text{R}}^{\text{2}}}}{\text{Z}_{\text{C}}^{\text{2}}}\text{+}\frac{\text{Z}_{\text{L}}^{\text{2}}}{\text{Z}_{\text{C}}^{\text{2}}}\text{-}\frac{\text{2}{{\text{Z}}_{\text{L}}}}{{{\text{Z}}_{\text{C}}}}\text{+1}}}$
= $\frac{\text{U}}{\sqrt{{{\text{L}}^{\text{2}}}{{\text{C}}^{\text{2}}}{{\text{
}\!\!\omega\!\!\text{ }}^{\text{4}}}\text{+}\left(
{{\text{R}}^{\text{2}}}{{\text{C}}^{\text{2}}}\text{-2LC} \right){{\text{
}\!\!\omega\!\!\text{ }}^{\text{2}}}\text{+1}}}$
Đặt x = ${{\text{
}\!\!\omega\!\!\text{ }}^{\text{2}}}$ $\Rightarrow $ ${{\text{U}}_{\text{C}}}$
= $\frac{\text{U}}{\sqrt{\text{f(x)}}}$ với f(x) = ${{\text{L}}^{\text{2}}}{{\text{C}}^{\text{2}}}{{\text{x}}^{\text{2}}}\text{+}\left(
{{\text{R}}^{\text{2}}}{{\text{C}}^{\text{2}}}\text{-2LC} \right)\text{x+1}$
Để ${{\text{U}}_{\text{C}}}$
max thì f(x) min tại
x = ${{\text{
}\!\!\omega\!\!\text{ }}^{\text{2}}}$ = - $\frac{\text{b}}{\text{2a}}$ = - $\frac{{{\text{R}}^{\text{2}}}{{\text{C}}^{\text{2}}}\text{-2LC}}{\text{2}{{\text{L}}^{\text{2}}}{{\text{C}}^{\text{2}}}}$
= $\frac{\text{2LC-}{{\text{R}}^{\text{2}}}{{\text{C}}^{\text{2}}}}{\text{2}{{\text{L}}^{\text{2}}}{{\text{C}}^{\text{2}}}}$
$\Rightarrow
$ $\text{ }\!\!\omega\!\!\text{ }$ = ${{\text{ }\!\!\omega\!\!\text{
}}_{\text{C}}}$ = $\sqrt{\frac{\text{2LC-}{{\text{R}}^{\text{2}}}{{\text{C}}^{\text{2}}}}{\text{2}{{\text{L}}^{\text{2}}}{{\text{C}}^{\text{2}}}}}$ $\Rightarrow $ $\text{f}{{\left( \text{x}
\right)}_{\text{min}}}$ = $\frac{\text{4}{{\text{R}}^{\text{2}}}\text{LC-}{{\text{R}}^{\text{4}}}{{\text{C}}^{\text{2}}}}{\text{4}{{\text{L}}^{\text{2}}}}$
$\Rightarrow
$ ${{\left( {{\text{U}}_{\text{C}}} \right)}_{\text{max}}}$ = $\frac{\text{U}}{\sqrt{\text{f(x}{{\text{)}}_{\text{min}}}}}$
= $\frac{\text{U}}{\sqrt{\frac{\text{4}{{\text{R}}^{\text{2}}}\text{LC-}{{\text{R}}^{\text{4}}}{{\text{C}}^{\text{2}}}}{\text{4}{{\text{L}}^{\text{2}}}}}}$
= $\frac{\text{2UL}}{\text{R}\sqrt{\text{4LC-}{{\text{R}}^{\text{2}}}{{\text{C}}^{\text{2}}}}}$
O Phát triển:
$\text{
}\!\!\omega\!\!\text{ }_{\text{C}}^{\text{2}}$ = $\frac{\text{2LC-}{{\text{R}}^{\text{2}}}{{\text{C}}^{\text{2}}}}{\text{2}{{\text{L}}^{\text{2}}}{{\text{C}}^{\text{2}}}}$
$\Rightarrow $ ${{\text{ }\!\!\omega\!\!\text{
}}^{\text{2}}}{{\text{L}}^{\text{2}}}$ = $\frac{\text{L}}{\text{C}}$ - $\frac{{{\text{R}}^{\text{2}}}}{\text{2}}$
$\Leftrightarrow
$ 2$\text{Z}_{\text{L}}^{\text{2}}$ = 2${{\text{Z}}_{\text{L}}}$.${{\text{Z}}_{\text{C}}}$
- ${{\text{R}}^{\text{2}}}$ $\Rightarrow $ ${{\text{R}}^{\text{2}}}$ = 2${{\text{Z}}_{\text{L}}}$(${{\text{Z}}_{\text{C}}}$
- ${{\text{Z}}_{\text{L}}}$)
$\Rightarrow
$ $\frac{{{\text{Z}}_{\text{L}}}}{\text{R}}$.$\frac{{{\text{Z}}_{\text{C}}}\text{-}{{\text{Z}}_{\text{L}}}}{\text{R}}$
= $\frac{1}{2}$ $\Leftrightarrow $ tan${{\text{ }\!\!\varphi\!\!\text{
}}_{\text{RL}}}$.tan$\text{ }\!\!\varphi\!\!\text{ }$ = $\frac{1}{2}$

$\mapsto $ ${{\text{U}}_{\text{Cmax}}}$
= $\frac{\text{U}}{\sqrt{\text{1-}\frac{\text{Z}_{\text{L}}^{\text{2}}}{\text{Z}_{\text{C}}^{\text{2}}}}}$
= $\frac{\text{U}}{\sqrt{\text{1-}\left(
\frac{{{\text{U}}_{\text{L}}}}{{{\text{U}}_{\text{Cmax}}}} \right)}}$
$\Rightarrow $ ${{\text{U}}^{\text{2}}}$
= $\text{U}_{\text{Cmax}}^{\text{2}}$ - $\text{U}_{\text{L}}^{\text{2}}$ ; ${{\text{Z}}^{\text{2}}}$
= $\text{Z}_{\text{C}}^{\text{2}}$ - $\text{Z}_{\text{L}}^{\text{2}}$
$\mapsto $Tóm lại khi khảo sát sự biến thiên của ${{\text{U}}_{\text{L}}}$, ${{\text{U}}_{\text{C}}}$ theo $\text{ }\!\!\omega\!\!\text{ }$ ta có:
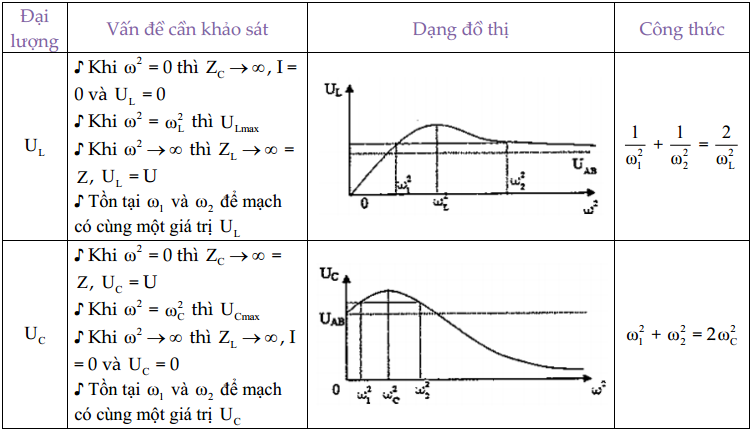
*
Mối liên hệ giữa ${{\text{ }\!\!\omega\!\!\text{ }}_{\text{L}}}$ và ${{\text{
}\!\!\omega\!\!\text{ }}_{\text{C}}}$:
${{\text{
}\!\!\omega\!\!\text{ }}_{\text{L}}}$.${{\text{ }\!\!\omega\!\!\text{
}}_{\text{C}}}$ = $\sqrt{\frac{\text{2}}{\text{2LC-}{{\text{R}}^{\text{2}}}{{\text{C}}^{\text{2}}}}}$.$\sqrt{\frac{\text{2LC-}{{\text{R}}^{\text{2}}}{{\text{C}}^{\text{2}}}}{\text{2}{{\text{L}}^{\text{2}}}{{\text{C}}^{\text{2}}}}}$
= $\frac{\text{1}}{\text{C}}$ .$\sqrt{\frac{\text{2}}{\frac{\text{2L}}{\text{C}}\text{-}{{\text{R}}^{\text{2}}}}}$
.$\frac{\text{1}}{\text{L}}$ .$\sqrt{\frac{\frac{\text{2L}}{\text{C}}\text{-}{{\text{R}}^{\text{2}}}}{2}}$
= $\frac{\text{1}}{\text{LC}}$ = ${{\text{ }\!\!\omega\!\!\text{
}}^{\text{2}}}$
Vậy ${{\text{ }\!\!\omega\!\!\text{
}}_{\text{L}}}$.${{\text{ }\!\!\omega\!\!\text{ }}_{\text{C}}}$ = $\frac{\text{1}}{\text{LC}}$ = ${{\text{
}\!\!\omega\!\!\text{ }}^{\text{2}}}$
II.
VÍ DỤ MINH HỌA
Ví dụ 1: Đặt u = ${{\text{U}}_{\text{0}}}\text{cos
}\!\!\omega\!\!\text{ t}$ V (${{\text{U}}_{\text{0}}}$ không đổi, $\text{
}\!\!\omega\!\!\text{ }$ thay đổi) vào hai đầu đoạn mạch gồm R, L = $\text{4/}\left(
\text{5 }\!\!\pi\!\!\text{ } \right)$ H và C mắc nối tiếp. Khi $\text{
}\!\!\omega\!\!\text{ }$ = ${{\text{ }\!\!\omega\!\!\text{ }}_{\text{0}}}$ thì
cường độ dòng điện hiệu dụng đạt giá trị cực địa ${{\text{I}}_{\text{m}}}$. Khi
$\text{ }\!\!\omega\!\!\text{ }$ = ${{\text{ }\!\!\omega\!\!\text{
}}_{\text{1}}}$ và $\text{ }\!\!\omega\!\!\text{ }$ = ${{\text{ }\!\!\omega\!\!\text{
}}_{\text{2}}}$ thì cường độ dòng điện cực đại qua mạch có giá trị bằng nhau và
bằng ${{\text{I}}_{\text{m}}}$. Biết ${{\text{ }\!\!\omega\!\!\text{
}}_{\text{1}}}$ - ${{\text{ }\!\!\omega\!\!\text{ }}_{\text{2}}}$ = $\text{200
}\!\!\pi\!\!\text{ }$ rad/s (${{\text{ }\!\!\omega\!\!\text{ }}_{\text{1}}}$
> ${{\text{ }\!\!\omega\!\!\text{ }}_{\text{2}}}$). Tính giá trị R.
Hướng
dẫn
${{\text{
}\!\!\omega\!\!\text{ }}_{\text{0}}}$ = $\frac{\text{1}}{\sqrt{\text{LC}}}$ $\Rightarrow
$ ${{\text{I}}_{\text{m}}}$ = $\frac{\text{U}}{\text{R}}$
Khi $\text{
}\!\!\omega\!\!\text{ }$ = ${{\text{ }\!\!\omega\!\!\text{ }}_{\text{1}}}$ và $\text{
}\!\!\omega\!\!\text{ }$ = ${{\text{ }\!\!\omega\!\!\text{ }}_{\text{2}}}$ thì
I = $\frac{{{\text{I}}_{\text{m}}}}{\sqrt{\text{2}}}$ = $\frac{\text{U}}{{{\text{Z}}_{1}}}$
= $\frac{\text{U}}{{{\text{Z}}_{\text{2}}}}$
$\Rightarrow
$ ${{\text{Z}}_{\text{1}}}$ = ${{\text{Z}}_{\text{2}}}$ = $\text{R}\sqrt{\text{2}}$
$\Rightarrow
$ ${{\text{R}}^{\text{2}}}$ + ${{\left(
{{\text{Z}}_{\text{L1}}}\text{-}{{\text{Z}}_{\text{C1}}} \right)}^{2}}$ = ${{\text{R}}^{\text{2}}}$
+ ${{\left( {{\text{Z}}_{\text{L2}}}\text{-}{{\text{Z}}_{\text{C2}}}
\right)}^{2}}$ = 2.${{\text{R}}^{\text{2}}}$
$\Rightarrow
$ ${{\text{Z}}_{\text{L1}}}$ - ${{\text{Z}}_{\text{C1}}}$ = ${{\text{Z}}_{\text{C2}}}$
- ${{\text{Z}}_{\text{L2}}}$ = R (1)
$\Rightarrow
$ ${{\text{ }\!\!\omega\!\!\text{ }}_{\text{1}}}$L - $\frac{\text{1}}{{{\text{
}\!\!\omega\!\!\text{ }}_{\text{1}}}\text{C}}$ = $\frac{\text{1}}{{{\text{
}\!\!\omega\!\!\text{ }}_{2}}\text{C}}$
- ${{\text{ }\!\!\omega\!\!\text{ }}_{\text{2}}}$L

$\Rightarrow
$ L = $\frac{\text{1}}{\text{C}{{\text{ }\!\!\omega\!\!\text{
}}_{\text{1}}}{{\text{ }\!\!\omega\!\!\text{ }}_{\text{2}}}}$ $\Rightarrow $ ${{\text{Z}}_{\text{L1}}}$
= ${{\text{Z}}_{\text{C2}}}$ ; ${{\text{Z}}_{\text{L2}}}$ = ${{\text{Z}}_{\text{C1}}}$ (2)
Ví dụ 2: Đặt điệp áp xoay chiều u = ${{\text{U}}_{\text{0}}}\text{cos
}\!\!\omega\!\!\text{ t}$ V (${{\text{U}}_{\text{0}}}$ không đổi, $\text{
}\!\!\omega\!\!\text{ }$ thay đổi) vào hai đầu đoạn mạch RLC với $\text{C}{{\text{R}}^{\text{2}}}$
> 2L. Khi $\text{ }\!\!\omega\!\!\text{ }$ = ${{\text{ }\!\!\omega\!\!\text{
}}_{\text{1}}}$ hoặc $\text{ }\!\!\omega\!\!\text{ }$ = ${{\text{
}\!\!\omega\!\!\text{ }}_{\text{2}}}$ thì điện áp hiệu dụng hai đầu tụ như
nhau. Khi $\text{ }\!\!\omega\!\!\text{ }$ = ${{\text{ }\!\!\omega\!\!\text{
}}_{\text{0}}}$ thì điện áp hai đầu tụ điện đạt giá trị cực đại. Tìm hệ thức
liên hệ giữa ${{\text{ }\!\!\omega\!\!\text{ }}_{\text{1}}}$, ${{\text{
}\!\!\omega\!\!\text{ }}_{\text{2}}}$ và ${{\text{ }\!\!\omega\!\!\text{
}}_{\text{0}}}$.
Hướng
dẫn
${{\text{U}}_{\text{C}}}$
= I.${{\text{Z}}_{\text{C}}}$ = $\frac{\text{U}\text{.}{{\text{Z}}_{\text{C}}}}{\text{Z}}$
= $\frac{\text{U}\text{.}{{\text{Z}}_{\text{C}}}}{\sqrt{{{\text{R}}^{\text{2}}}\text{+}{{\left(
{{\text{Z}}_{\text{L}}}\text{-}{{\text{Z}}_{\text{C}}} \right)}^{\text{2}}}}}$
= $\frac{\text{U}}{\sqrt{\frac{{{\text{R}}^{\text{2}}}}{\text{Z}_{\text{C}}^{\text{2}}}\text{+}\frac{\text{Z}_{\text{L}}^{\text{2}}}{\text{Z}_{\text{C}}^{\text{2}}}\text{-}\frac{\text{2}{{\text{Z}}_{\text{L}}}}{{{\text{Z}}_{\text{C}}}}\text{+1}}}$
= $\frac{\text{U}}{\sqrt{{{\text{L}}^{\text{2}}}{{\text{C}}^{\text{2}}}{{\text{
}\!\!\omega\!\!\text{ }}^{\text{4}}}\text{+}\left(
{{\text{R}}^{\text{2}}}{{\text{C}}^{\text{2}}}\text{-2LC} \right){{\text{
}\!\!\omega\!\!\text{ }}^{\text{2}}}\text{+1}}}$
Đặt x = ${{\text{
}\!\!\omega\!\!\text{ }}^{\text{2}}}$ $\Rightarrow $ ${{\text{U}}_{\text{C}}}$
= $\frac{\text{U}}{\sqrt{\text{f(x)}}}$ với f(x) = ${{\text{L}}^{\text{2}}}{{\text{C}}^{\text{2}}}{{\text{x}}^{\text{2}}}\text{+}\left(
{{\text{R}}^{\text{2}}}{{\text{C}}^{\text{2}}}\text{-2LC} \right)\text{x+1}$
Để ${{\text{U}}_{\text{C}}}$
max thì f(x) min tại
x = ${{\text{x}}_{\text{0}}}$
= $\text{ }\!\!\omega\!\!\text{ }_{0}^{2}$ = - $\frac{\text{b}}{\text{2a}}$( =
- $\frac{{{\text{R}}^{\text{2}}}{{\text{C}}^{\text{2}}}\text{-2LC}}{\text{2}{{\text{L}}^{\text{2}}}{{\text{C}}^{\text{2}}}}$
= $\frac{\text{2LC-}{{\text{R}}^{\text{2}}}{{\text{C}}^{\text{2}}}}{\text{2}{{\text{L}}^{\text{2}}}{{\text{C}}^{\text{2}}}}$)
Khi $\text{
}\!\!\omega\!\!\text{ }$ = ${{\text{ }\!\!\omega\!\!\text{ }}_{\text{1}}}$ hoặc
$\text{ }\!\!\omega\!\!\text{ }$ = ${{\text{ }\!\!\omega\!\!\text{
}}_{\text{2}}}$ thì như nhau:
${{\text{x}}_{\text{1}}}$ + ${{\text{x}}_{\text{2}}}$ = $\text{-}\frac{\text{b}}{\text{a}}$ = $\text{2}{{\text{x}}_{\text{0}}}$ $\Rightarrow $ $\text{ }\!\!\omega\!\!\text{ }_{\text{1}}^{\text{2}}$ + $\text{ }\!\!\omega\!\!\text{ }_{\text{2}}^{\text{2}}$ = 2$\text{ }\!\!\omega\!\!\text{ }_{\text{0}}^{\text{2}}$
Ví dụ 3: Đặt u =$\text{120}\sqrt{\text{2}}$cos$\text{2
}\!\!\pi\!\!\text{ ft}$ V (f thay đổi) vào hai đầu đoạn mạch RLC mắc nối tiếp với
$\text{C}{{\text{R}}^{\text{2}}}$ > 2L. Khi f = ${{\text{f}}_{\text{1}}}$
thì điện áp hai đầu tụ điện đạt giá trị cực đại. Khi f = ${{\text{f}}_{\text{1}}}\sqrt{\text{2}}$
thì điện áp hai đầu điện trở đạt giá trị cực đại. Khi f = ${{\text{f}}_{\text{2}}}$
thì điện áp hai đầu cuộn cảm đạt giá trị cực đại ${{\text{U}}_{\text{Lmax}}}$ .
Tính giá trị ${{\text{U}}_{\text{Lmax}}}$.
Hướng
dẫn
Áp dụng
công thức: ${{\text{ }\!\!\omega\!\!\text{ }}_{\text{L}}}$.${{\text{
}\!\!\omega\!\!\text{ }}_{\text{C}}}$ = $\text{ }\!\!\omega\!\!\text{
}_{\text{0}}^{\text{2}}$ $\Rightarrow $ ${{\text{f}}_{\text{L}}}$.${{\text{f}}_{\text{C}}}$
= ${{\text{f}}^{\text{2}}}$
$\Leftrightarrow
$ ${{\text{f}}_{\text{2}}}$.${{\text{f}}_{\text{1}}}$ = ${{\left(
{{\text{f}}_{\text{1}}}\sqrt{\text{2}} \right)}^{\text{2}}}$ $\Rightarrow $ ${{\text{f}}_{\text{2}}}$ = $\text{2}{{\text{f}}_{\text{1}}}$
${{\text{U}}_{\text{Lmax}}}$
= $\frac{\text{2UL}}{\text{R}\sqrt{\text{4LC-}{{\text{R}}^{\text{2}}}{{\text{C}}^{\text{2}}}}}$=
$\frac{\text{U}}{\sqrt{\text{1-}{{\left( \frac{{{\text{ }\!\!\omega\!\!\text{
}}_{\text{C}}}}{{{\text{ }\!\!\omega\!\!\text{ }}_{\text{L}}}}
\right)}^{\text{2}}}}}$ = $\frac{\text{U}}{\sqrt{\text{1-}\left(
\frac{{{\text{f}}_{\text{1}}}}{\text{2}{{\text{f}}_{\text{1}}}} \right)}}$ = $\frac{\text{2U}}{\sqrt{\text{3}}}$
= $\frac{2.120}{\sqrt{3}}$ = $80\sqrt{3}$ (V)
Ví dụ 4: Đặt u =$\text{U}\sqrt{\text{2}}$cos$\text{2
}\!\!\pi\!\!\text{ ft}$ V (U không đổi, f thay đổi) vào hai đầu đoạn mạch RLC mắc
nối tiếp với $\text{C}{{\text{R}}^{\text{2}}}$ > 2L. Chỉnh f để điện áp hai
đầu cuộn cảm đạt giá trị cực đại ${{\text{U}}_{\text{Lmax}}}$. Khi đó ${{\text{U}}_{\text{Lmax}}}$
= $\frac{41}{40}$U. Tính hệ số công suất của đoạn mạch.
Hướng
dẫn
${{\text{U}}_{\text{Lmax}}}$
= $\frac{\text{U}}{\sqrt{\text{1-}{{\left( \frac{{{\text{ }\!\!\omega\!\!\text{
}}_{\text{C}}}}{{{\text{ }\!\!\omega\!\!\text{ }}_{\text{L}}}}
\right)}^{\text{2}}}}}$ = $\frac{41}{40}$U $\Rightarrow $ $\sqrt{\text{1-}{{\left(
\frac{{{\text{ }\!\!\omega\!\!\text{ }}_{\text{C}}}}{{{\text{
}\!\!\omega\!\!\text{ }}_{\text{L}}}} \right)}^{\text{2}}}}$ = $\frac{40}{41}$
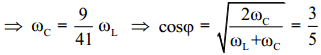
Ví dụ 5: Đặt u =$\text{U}\sqrt{\text{2}}$cos$\text{2
}\!\!\pi\!\!\text{ ft}$ V (U không đổi, f thay đổi) vào hai đầu đoạn mạch RLC mắc
nối tiếp với $\text{C}{{\text{R}}^{\text{2}}}$ > 2L. Khi f = ${{\text{f}}_{\text{1}}}$
thì điện áp dai đầu tụ điện đạt giá trị cực đại và công suất tiêu thụ trên đoạn
mạch bằng 3/4 công suất tiêu thụ cực đại. Khi f = ${{\text{f}}_{\text{2}}}$ = (${{\text{f}}_{\text{1}}}$
+ 100) Hz thì điện áp hai đầu cuộn cảm đạt giá trị cực đại. Tính tần số f = ${{\text{f}}_{\text{3}}}$
để điện áp hai đầu điện trở đạt giá trị cực đại.
Hướng
dẫn
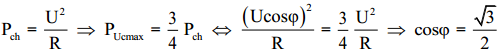
$\Leftrightarrow
$ $\sqrt{\frac{\text{2}{{\text{f}}_{\text{1}}}}{{{\text{f}}_{\text{1}}}\text{+100}}}$
= $\frac{\sqrt{3}}{2}$ $\Rightarrow $ ${{\text{f}}_{\text{1}}}$ = 150 (Hz)
${{\text{f}}_{\text{2}}}$
= ${{\text{f}}_{\text{1}}}$ + 100 = 250 (Hz)
$\text{f}_{\text{3}}^{\text{2}}$
= ${{\text{f}}_{\text{1}}}$.${{\text{f}}_{\text{2}}}$ $\Rightarrow $ ${{\text{f}}_{\text{3}}}$
= $\sqrt{150.250}$ = $50\sqrt{15}$ (Hz)
III.
BÀI TẬP TỰ LUYỆN
Bài
1: Đặt điện áp xoay chiều u = $200\sqrt{2}$cos$\text{2
}\!\!\pi\!\!\text{ ft}$ V (f thay đổi được) vào hai đầu đoạn mạch có R = 50 $\text{
}\!\!\Omega\!\!\text{ }$, cuộn cảm thuần L = $\text{2/ }\!\!\pi\!\!\text{ }$ H
và tụ điện C = 2.$\text{1}{{\text{0}}^{\text{-4}}}\text{/ }\!\!\pi\!\!\text{ }$
F mắc nối tiếp. Khi điều chỉnh tần số f để cường độ dòng điện hiệu dụng qua đoạn
mạch bằng 4 A thì giá trị của f là
A. 100 Hz B. 25 Hz C. 50 Hz D. 40 Hz
Bài
2: Đặt điện áp xoay chiều u = $\text{U}\sqrt{\text{2}}$cos$\text{2
}\!\!\pi\!\!\text{ ft}$ V ($\text{U}$ không đổi và f thay đổi được) vào hai đầu
đoạn mạch có R, L, C mắc nối tiếp. Khi f = ${{\text{f}}_{\text{0}}}$ thì trong
đoạn mạch có cộng hưởng điện. Giá trị của ${{\text{f}}_{\text{0}}}$ là
A. $\frac{\text{2}}{\sqrt{\text{LC}}}$ B. $\frac{\text{2 }\!\!\pi\!\!\text{ }}{\sqrt{\text{LC}}}$ C. $\frac{\text{1}}{\sqrt{\text{LC}}}$ D. $\frac{\text{1}}{\text{2 }\!\!\pi\!\!\text{
}\sqrt{\text{LC}}}$
Bài
3: Đặt điện áp xoay chiều u = $\text{U}\sqrt{\text{2}}$cos$\text{
}\!\!\omega\!\!\text{ t}$ V ($\text{U}$ không đổi và $\text{
}\!\!\omega\!\!\text{ }$ thay đổi được) vào hai đầu đoạn mạch có R, L, C mắc nối
tiếp. Khi $\text{ }\!\!\omega\!\!\text{ }$ = ${{\text{ }\!\!\omega\!\!\text{
}}_{\text{0}}}$ thì công suất tiêu thụ của mạch đạt cực đại ${{\text{P}}_{\text{max}}}$.
Khi đó ${{\text{P}}_{\text{max}}}$ được xác định bởi biểu thức
A.
${{\text{P}}_{\text{max}}}$
= $\frac{{{\text{U}}^{\text{2}}}}{\text{R}}$ B. ${{\text{P}}_{\text{max}}}$ = $\text{I}_{\text{0}}^{\text{2}}\text{R}$
C. ${{\text{P}}_{\text{max}}}$
= $\frac{{{\text{U}}^{\text{2}}}}{{{\text{R}}^{2}}}$ D. ${{\text{P}}_{\text{max}}}$
= $\frac{{{\text{U}}^{\text{2}}}}{\text{2R}}$
Bài
4: Đặt điện áp xoay chiều u = ${{\text{U}}_{\text{0}}}$cos$\text{
}\!\!\omega\!\!\text{ t}$ V (${{\text{U}}_{\text{0}}}$ không đổi và $\text{
}\!\!\omega\!\!\text{ }$ thay đổi được) vào hai đầu đoạn mạch có R, L, C mắc nối
tiếp. Khi $\text{ }\!\!\omega\!\!\text{ }$ = ${{\text{ }\!\!\omega\!\!\text{
}}_{1}}$ thì cảm kháng của cuộn cảm thuần bằng 4 lần dung kháng của tụ điện.
Khi $\text{ }\!\!\omega\!\!\text{ }$ = ${{\text{ }\!\!\omega\!\!\text{ }}_{2}}$
thì trong mạch xảy ra hiện tượng cộng hưởng điện. Hệ thức đúng là
A.
${{\text{ }\!\!\omega\!\!\text{ }}_{1}}$ = 2${{\text{ }\!\!\omega\!\!\text{ }}_{2}}$ B. 2${{\text{ }\!\!\omega\!\!\text{ }}_{1}}$ = ${{\text{
}\!\!\omega\!\!\text{ }}_{2}}$ C. ${{\text{ }\!\!\omega\!\!\text{ }}_{1}}$ = 4${{\text{
}\!\!\omega\!\!\text{ }}_{2}}$ D. 4${{\text{ }\!\!\omega\!\!\text{ }}_{1}}$ = ${{\text{
}\!\!\omega\!\!\text{ }}_{2}}$
Bài
5: Đặt điện áp xoay chiều u = ${{\text{U}}_{\text{0}}}$cos$\text{
}\!\!\omega\!\!\text{ t}$ V (${{\text{U}}_{\text{0}}}$ không đổi và $\text{
}\!\!\omega\!\!\text{ }$ thay đổi được) vào hai đầu đoạn mạch có R, L, C mắc nối
tiếp. Thay đổi $\text{ }\!\!\omega\!\!\text{ }$ thì cường độ dòng điện hiệu dụng
trong mạch khi $\text{ }\!\!\omega\!\!\text{ }$ = ${{\text{
}\!\!\omega\!\!\text{ }}_{\text{1}}}$ bằng cường độ dòng điện hiệu dụng trong mạch
khi $\text{ }\!\!\omega\!\!\text{ }$ = ${{\text{ }\!\!\omega\!\!\text{
}}_{\text{2}}}$. Chọn hệ thức đúng.
A. ${{\text{ }\!\!\omega\!\!\text{ }}_{\text{1}}}$ + ${{\text{ }\!\!\omega\!\!\text{ }}_{\text{2}}}$ = $\frac{\text{2}}{\sqrt{\text{LC}}}$ B. ${{\text{ }\!\!\omega\!\!\text{ }}_{\text{1}}}$.${{\text{ }\!\!\omega\!\!\text{ }}_{\text{2}}}$ = $\frac{\text{1}}{\text{LC}}$ C. ${{\text{ }\!\!\omega\!\!\text{ }}_{\text{1}}}$ + ${{\text{ }\!\!\omega\!\!\text{ }}_{\text{2}}}$ = $\frac{\text{2}}{\text{LC}}$ D. ${{\text{ }\!\!\omega\!\!\text{ }}_{\text{1}}}$.${{\text{ }\!\!\omega\!\!\text{ }}_{\text{2}}}$ = $\frac{\text{1}}{\sqrt{\text{LC}}}$
Bài
6: Đặt điện áp xoay chiều u = ${{\text{U}}_{\text{0}}}$cos$\text{
}\!\!\omega\!\!\text{ t}$ V (${{\text{U}}_{\text{0}}}$ không đổi và $\text{
}\!\!\omega\!\!\text{ }$ thay đổi được) vào hai đầu đoạn mạch có R, L, C mắc nối
tiếp. Khi $\text{ }\!\!\omega\!\!\text{ }$ = ${{\text{ }\!\!\omega\!\!\text{
}}_{\text{1}}}$ = $\text{100}\sqrt{\text{2}}\text{ }\!\!\pi\!\!\text{ }$ rad/s thì
công suất tiêu thụ của đoạn mạch cực đại. Khi $\text{ }\!\!\omega\!\!\text{ }$
= ${{\text{ }\!\!\omega\!\!\text{ }}_{\text{2}}}$ thì cảm kháng của cuộn cảm bằng
15 $\Omega $ và dung kháng của tụ bằng
30 $\Omega $. Độ tự cảm L có giá trị
A. $\frac{\text{0,45}}{\text{
}\!\!\pi\!\!\text{ }}$ H B. $\frac{\text{0,6}}{\text{
}\!\!\pi\!\!\text{ }}$ H C. $\frac{\text{0,15}}{\text{
}\!\!\pi\!\!\text{ }}$ H D. $\frac{\text{0,3}}{\text{
}\!\!\pi\!\!\text{ }}$ H
Bài
7: Đặt điện áp xoay chiều u = ${{\text{U}}_{\text{0}}}$cos$\text{
}\!\!\omega\!\!\text{ t}$ V (${{\text{U}}_{\text{0}}}$ không đổi và $\text{
}\!\!\omega\!\!\text{ }$ thay đổi được) vào hai đầu đoạn mạch RLC mắc nối tiếp.
Khi f = ${{\text{f}}_{\text{1}}}$ thì mạch có cảm kháng là 36 $\Omega $ và dung
kháng là 144 $\Omega $. Khi f = ${{\text{f}}_{\text{2}}}$ = 120 Hz thì cường độ
dòng điện cùng pha với điện áp ở hai đầu đoạn mạch. Giá trị của tần số ${{\text{f}}_{\text{1}}}$
là
A. 50 Hz B. 60 Hz C. 85 Hz D. 100 Hz
Bài
8: Đoạn mạch xoay chiều RLC, cuộn dây thuần
cảm, biết L = $\text{C}{{\text{R}}^{\text{2}}}$. Đặt vào hai đầu đoạn mạch điện
áp xoay chiều ổn định, với tần số góc $\text{ }\!\!\omega\!\!\text{ }$ thay đổi,
trong mạch có cùng hệ số công suất với hai tần số góc là ${{\text{
}\!\!\omega\!\!\text{ }}_{\text{1}}}$ = $\text{50 }\!\!\pi\!\!\text{ }$ rad/s
và ${{\text{ }\!\!\omega\!\!\text{ }}_{\text{2}}}$ = $\text{200
}\!\!\pi\!\!\text{ }$ rad/s. Hệ số công suất của mạch là
A.
$\frac{8}{17}$
B. $\frac{2}{\sqrt{13}}$ C. $\frac{3}{\sqrt{11}}$
D. $\frac{5}{\sqrt{57}}$
Bài
9: Đặt u = ${{\text{U}}_{\text{0}}}\text{cos
}\!\!\omega\!\!\text{ t}$ V (${{\text{U}}_{\text{0}}}$ không đổi, $\text{
}\!\!\omega\!\!\text{ }$ có thể thay đổi) vào hai đầu đoạn mạch gồm R, L = $\text{4/}\left(
\text{5 }\!\!\pi\!\!\text{ } \right)$ H và C mắc nối tiếp. Khi $\text{
}\!\!\omega\!\!\text{ }$ = ${{\text{ }\!\!\omega\!\!\text{ }}_{\text{0}}}$ thì
cường độ dòng điện hiệu dụng đạt giá trị cực địa ${{\text{I}}_{\text{m}}}$. Khi
$\text{ }\!\!\omega\!\!\text{ }$ = ${{\text{ }\!\!\omega\!\!\text{
}}_{\text{1}}}$ và $\text{ }\!\!\omega\!\!\text{ }$ = ${{\text{
}\!\!\omega\!\!\text{ }}_{\text{2}}}$ thì cường độ dòng điện cực đại qua mạch
có giá trị bằng nhau và bằng ${{\text{I}}_{\text{m}}}$. Biết ${{\text{
}\!\!\omega\!\!\text{ }}_{\text{1}}}$ - ${{\text{ }\!\!\omega\!\!\text{
}}_{\text{2}}}$ = $\text{200 }\!\!\pi\!\!\text{ }$ rad/s (${{\text{
}\!\!\omega\!\!\text{ }}_{\text{1}}}$ > ${{\text{ }\!\!\omega\!\!\text{
}}_{\text{2}}}$). Tính giá trị R.
A.
160 $\Omega $ B. 200 $\Omega $ C. 50 $\Omega $ D. 150 $\Omega $
Bài
10: Đặt vào hai đầu đoạn mạch RLC nối tiếp
một điện áp xoay chiều có tần số f thay đổi được. Khi f = ${{\text{f}}_{\text{1}}}$
thì hệ số công suất $\text{cos}{{\text{ }\!\!\varphi\!\!\text{ }}_{\text{1}}}$
= 1. Khi f = 2${{\text{f}}_{\text{1}}}$ thì hệ số công suất là $\text{cos}{{\text{
}\!\!\varphi\!\!\text{ }}_{\text{2}}}$ = 0,707. Khi f = 1,5${{\text{f}}_{\text{1}}}$
thì hệ số công suất là
A.
0,625 B. 0,874 C. 0,486 D. 0,546
Bài
11: Đặt điệp áp xoay chiều u = $100\sqrt{2}$cos$\text{
}\!\!\omega\!\!\text{ t}$ $\text{ }\!\!\omega\!\!\text{ }$ thay đổi được) vào
hai đầu đoạn mạch có R = $50\sqrt{2}$ $\Omega $, cuộn cảm thuần L = $\text{1/
}\!\!\pi\!\!\text{ }$ H và tụ điện C = $\text{1}{{\text{0}}^{\text{-4}}}\text{/
}\!\!\pi\!\!\text{ }$ F mắc nối tiếp. Thay đổi $\text{ }\!\!\omega\!\!\text{ }$
thì điện áp hiệu dụng giữa hai đầu cuộn cảm đạt giá trị cực đại ${{\text{U}}_{\text{Lmax}}}$.
Giá trị của ${{\text{U}}_{\text{Lmax}}}$ là
A. $\frac{100}{\sqrt{7}}$ V B. $\frac{600}{\sqrt{7}}$ V C. $\frac{200}{\sqrt{7}}$
V D. $\frac{400}{\sqrt{7}}$ V
Bài
12: Đặt điện áp xoay chiều u = ${{\text{U}}_{\text{0}}}$cos$\text{
}\!\!\omega\!\!\text{ t}$ V (${{\text{U}}_{\text{0}}}$ không đổi và $\text{
}\!\!\omega\!\!\text{ }$ thay đổi được) vào hai đầu đoạn mạch gồm điện trở thuần
R, cuộn cảm thuần có độ tự cảm L và tụ điện có điện dung C mắc nối tiếp với $\text{C}{{\text{R}}^{\text{2}}}$
< 2L. Thay đổi $\text{ }\!\!\omega\!\!\text{ }$ đến giá trị mà điện áp hiệu
dụng giữa hai đầu cuộn cảm đạt cực đại là ${{\text{U}}_{\text{Lmax}}}$ khi đó,
cảm kháng và dung kháng của mạch là ${{\text{Z}}_{\text{L}}}$ và ${{\text{Z}}_{\text{C}}}$.
Giá trị ${{\text{U}}_{\text{Lmax}}}$ có biểu thức
A. ${{\text{U}}_{\text{Lmax}}}$ = \[\frac{\text{U}}{\sqrt{\text{1-}\frac{\text{Z}_{\text{C}}^{\text{2}}}{\text{Z}_{\text{L}}^{\text{2}}}}}\]
B. ${{\text{U}}_{\text{Lmax}}}$ = $\frac{\text{2UL}}{\sqrt{\text{4LC-}{{\text{R}}^{\text{2}}}{{\text{C}}^{\text{2}}}}}$
C. ${{\text{U}}_{\text{Lmax}}}$ = \[\frac{\text{U}}{\sqrt{\text{1-}\frac{\text{Z}_{\text{L}}^{\text{2}}}{\text{Z}_{\text{C}}^{\text{2}}}}}\] D. ${{\text{U}}_{\text{Lmax}}}$ = $\frac{\text{2UL}}{\text{R}\sqrt{\text{4LC-}{{\text{R}}^{\text{2}}}{{\text{C}}^{\text{2}}}}}$
Bài
13: Đặt điện áp xoay chiều u = ${{\text{U}}_{\text{0}}}$cos$\text{
}\!\!\omega\!\!\text{ t}$ V (${{\text{U}}_{\text{0}}}$ không đổi và $\text{
}\!\!\omega\!\!\text{ }$ thay đổi được) vào hai đầu đoạn mạch gồm điện trở thuần
R, cuộn cảm thuần có độ tự cảm L và tụ điện có điện dung C mắc nối tiếp với $\text{C}{{\text{R}}^{\text{2}}}$
< 2L. Khi $\text{ }\!\!\omega\!\!\text{ }$ = ${{\text{ }\!\!\omega\!\!\text{
}}_{\text{1}}}$ = 45 rad/s hoặc $\text{ }\!\!\omega\!\!\text{ }$ = ${{\text{
}\!\!\omega\!\!\text{ }}_{\text{2}}}$ = 60 rad/s thì điện áp hiệu dụng giữa hai
bản tụ điện có cùng một giá trị. Để điện áp hiệu dụng giữa hai đầu tụ điện đạt
cực đại thì tần số giá trị bằng
A. 8,44 Hz B. 8,1 Hz C. $36\sqrt{2}$ Hz D. 75 Hz
Bài
14: Đặt điện áp xoay chiều u = 200 cos$\text{
}\!\!\omega\!\!\text{ t}$ V vào hai đầu đoạn mạch gồm điện trở thuần R = $50\sqrt{3}$
$\Omega $, cuộn cảm thuần có độ tự cảm L = $\text{1/2 }\!\!\pi\!\!\text{ }$ H
và tụ điện có điện dung C = $\text{1}{{\text{0}}^{\text{-4}}}\text{/2
}\!\!\pi\!\!\text{ }$ F mắc nối tiếp. Thay đổi tần số để điện áp hiệu dụng giữa
hai bản tụ điện đạt cực đại. Khi đó, hệ số công suất của đoạn mạch là
A. 0,6 B. 0,8 C. 0,5 D. 0,7
Bài
15: Đặt điện áp xoay chiều u = ${{\text{U}}_{\text{0}}}$cos$\text{
}\!\!\omega\!\!\text{ t}$ V (${{\text{U}}_{\text{0}}}$ không đổi và $\text{
}\!\!\omega\!\!\text{ }$ thay đổi được) vào hai đầu đoạn mạch gồm điện trở thuần
R, cuộn cảm thuần có độ tự cảm L và tụ điện có điện dung C mắc nối tiếp. Khi ${{\text{
}\!\!\omega\!\!\text{ }}_{\text{1}}}$ = $\text{50 }\!\!\pi\!\!\text{ }$ rad/s
hoặc ${{\text{ }\!\!\omega\!\!\text{ }}_{\text{2}}}$ = $\text{200
}\!\!\pi\!\!\text{ }$ rad/s thì công suất của mạch có cùng giá trị. Giá trị của
$\text{ }\!\!\omega\!\!\text{ }$ để công suất trên mạch đạt cực đại là
A.
$\text{100 }\!\!\pi\!\!\text{ }$ rad/s B. $\text{150 }\!\!\pi\!\!\text{ }$ rad/s C. $\text{125 }\!\!\pi\!\!\text{
}$ rad/s D. $\text{175
}\!\!\pi\!\!\text{ }$ rad/s
Bài
16: Cho mạch xoay chiều không phân nhánh
RLC có tần số dòng điện thay đổi được. Gọi ${{\text{f}}_{\text{0}}}$, ${{\text{f}}_{\text{1}}}$
và ${{\text{f}}_{\text{2}}}$ lần lượt là các giá trị của tần số dòng điện làm
cho ${{\text{U}}_{\text{Rmax}}}$, ${{\text{U}}_{\text{Lmax}}}$ và ${{\text{U}}_{\text{Cmax}}}$.
Khi đó
A.
$\frac{{{\text{f}}_{\text{1}}}}{{{\text{f}}_{\text{0}}}}$ = $\frac{{{\text{f}}_{\text{0}}}}{{{\text{f}}_{\text{2}}}}$
B. ${{\text{f}}_{\text{0}}}$
+ ${{\text{f}}_{\text{1}}}$ = ${{\text{f}}_{\text{2}}}$ C. ${{\text{f}}_{\text{0}}}$ = $\frac{{{\text{f}}_{\text{1}}}}{{{\text{f}}_{\text{2}}}}$
D. $\text{f}_{0}^{2}$
= $\frac{{{\text{f}}_{\text{1}}}}{{{\text{f}}_{\text{2}}}}$
Bài
17: Đặt điện áp xoay chiều u = 200 cos$\text{
}\!\!\omega\!\!\text{ t}$ V vào hai đầu đoạn mạch gồm điện trở thuần R = $50\sqrt{3}$
$\Omega $, cuộn cảm thuần có độ tự cảm L = $\text{1/2 }\!\!\pi\!\!\text{ }$ H
và tụ điện có điện dung C = $\text{1}{{\text{0}}^{\text{-4}}}\text{/2
}\!\!\pi\!\!\text{ }$ F mắc nối tiếp. Khi $\text{ }\!\!\omega\!\!\text{ }$ = ${{\text{
}\!\!\omega\!\!\text{ }}_{\text{L}}}$ thì điện áp hiệu dụng giữa hai đầu cuộn cảm
đạt cực đại. Giá trị của ${{\text{ }\!\!\omega\!\!\text{ }}_{\text{L}}}$ là
A.
$\text{300 }\!\!\pi\!\!\text{ }$ rad/s B. $\text{200 }\!\!\pi\!\!\text{ }$ rad/s C. $\text{400 }\!\!\pi\!\!\text{
}$ rad/s D. $\text{100
}\!\!\pi\!\!\text{ }$ rad/s
Bài 18: Đặt điện áp xoay chiều u = ${{\text{U}}_{\text{0}}}$cos$\text{ }\!\!\omega\!\!\text{ t}$ V (${{\text{U}}_{\text{0}}}$ không đổi và $\text{ }\!\!\omega\!\!\text{ }$ thay đổi được) vào hai đầu đoạn mạch gồm điện trở thuần R = $20\sqrt{2}$ $\Omega $, cuộn cảm thuần có độ tự cảm L = $\text{4/}\left( \text{5 }\!\!\pi\!\!\text{ } \right)$ H và tụ điện có điện dung C = $\text{1}{{\text{0}}^{\text{-3}}}\text{/}\left( \text{2 }\!\!\pi\!\!\text{ } \right)$ F mắc nối tiếp. Khi $\text{ }\!\!\omega\!\!\text{ }$ = ${{\text{ }\!\!\omega\!\!\text{ }}_{\text{1}}}$ thì ${{\text{U}}_{\text{Lmax}}}$; $\text{ }\!\!\omega\!\!\text{ }$ = ${{\text{ }\!\!\omega\!\!\text{ }}_{\text{2}}}$ thì ${{\text{U}}_{\text{Cmax}}}$. Khi $\text{ }\!\!\omega\!\!\text{ }$ = ${{\text{ }\!\!\omega\!\!\text{ }}_{\text{1}}}$ + ${{\text{ }\!\!\omega\!\!\text{ }}_{\text{2}}}$ thì hệ số công suất của mạch bằng
A. 0,8 B. 0,58 C. 0,08 D. 0,057
Bài
19: Đoạn mạch xoay chiều RLC nối tiếp, cuộn
dây thuần cảm với $\text{C}{{\text{R}}^{\text{2}}}$ < 2L; điện áp hai đầu đoạn
mạch là u = ${{\text{U}}_{\text{0}}}$cos$\text{ }\!\!\omega\!\!\text{ t}$ V (${{\text{U}}_{\text{0}}}$
không đổi và $\text{ }\!\!\omega\!\!\text{ }$ thay đổi được). Khi $\text{
}\!\!\omega\!\!\text{ }$ = ${{\text{ }\!\!\omega\!\!\text{ }}_{\text{C}}}$ thì
điện áp hai đầu tụ điện đạt cực đại và điện áp hiệu dụng hai đầu cuộn dây ${{\text{U}}_{\text{L}}}$
= $\frac{{{\text{U}}_{\text{R}}}}{10}$. Hệ số công suất tiêu thụ của cả đoạn mạch
là
A. 0,6 B. $\frac{1}{\sqrt{15}}$ C. $\frac{1}{\sqrt{26}}$
D. 0,8
Bài
20: Đoạn mạch xoay chiều RLC nối tiếp, cuộn
dây thuần cảm với $\text{C}{{\text{R}}^{\text{2}}}$ < 2L; điện áp hai đầu đoạn
mạch là u = ${{\text{U}}_{\text{0}}}$cos$\text{2 }\!\!\pi\!\!\text{ ft}$ V (${{\text{U}}_{\text{0}}}$
không đổi và f thay đổi được). Khi f = ${{\text{f}}_{\text{1}}}$ thì ${{\text{U}}_{\text{Cmax}}}$
và công suất của mạch là P = 0,75${{\text{P}}_{\text{max}}}$. Khi f = ${{\text{f}}_{\text{2}}}$
= ${{\text{f}}_{\text{1}}}$ + 100 Hz thì ${{\text{U}}_{\text{Lmax}}}$. Giá trị ${{\text{f}}_{\text{1}}}$,
${{\text{f}}_{\text{2}}}$ lần lượt là
A. 150Hz, 250Hz B. 50Hz, 150Hz C. 250Hz, 350Hz D. 50Hz, 250Hz
Bài
21: Cho mạch điện xoay chiều AB theo thứ tự
gồm điện trở thuần R, cuộn dây thuần cảm L, tụ điện C mắc nối tiếp. N là điểm nằm
giữa cuộn dây và tụ điện. Đặt vào hai đầu đoạn mạch điện áp xoay chiều có biểu
thức u = ${{\text{U}}_{\text{0}}}$cos$\text{ }\!\!\omega\!\!\text{ t}$ V (${{\text{U}}_{\text{0}}}$
không đổi và $\text{ }\!\!\omega\!\!\text{ }$ thay đổi được). Điểu chỉnh $\text{
}\!\!\omega\!\!\text{ }$ để điện áp hiệu dụng trên tụ có giá trị cực đại, khi
đó ${{\text{u}}_{\text{AN}}}$ lệch pha $\text{2
}\!\!\pi\!\!\text{ /5}$ rad so với ${{\text{u}}_{\text{AB}}}$, công suất tiêu
thụ của mạch khi đó là 100 W và hệ số công suất của đoạn mạch AN lớn hơn hệ số
công suất của đoạn mạch AB. Khi điều chỉnh $\text{ }\!\!\omega\!\!\text{ }$ để
công suất tiêu thụ của mạch đạt cực đại và giá trị cực đại đó bằng
A. $100\sqrt{2}$ W B. 100 W C. 215 W D. $200\sqrt{3}$ W
Bài
22: Đặt một điện áp u = $\text{U}\sqrt{\text{2}}$cos$\text{2
}\!\!\pi\!\!\text{ ft}$ V vào hai đầu đọan mạch RLC mắc nối tiếp. Khi tần số f
= ${{\text{f}}_{\text{1}}}$, f = ${{\text{f}}_{\text{1}}}$ + 150 Hz, f = ${{\text{f}}_{\text{1}}}$
+ 50 Hz thì hệ số công suất của mạch tương ứng là 1; 0,6 và 15/17. Tần số để mạch
cộng hưởng gần giá trị nào sau đây nhất?
A. 180Hz B. 150 Hz C. 120 Hz D. 100 Hz
Bài
23: Đặt một điện áp u = $\text{U}\sqrt{\text{2}}$cos$\text{2
}\!\!\pi\!\!\text{ ft}$ V vào hai đầu đọan mạch RLC mắc nối tiếp với $\text{C}{{\text{R}}^{\text{2}}}$
< 2L. Khi f = ${{\text{f}}_{\text{1}}}$ thì ${{\text{U}}_{\text{L}}}$ = U và
công suất tiêu thụ bằng 0,75 lần công suất cực đại. Khi f = ${{\text{f}}_{\text{2}}}$
= ${{\text{f}}_{\text{1}}}$ - 100 Hz thì ${{\text{U}}_{\text{C}}}$ = U. Khi f =
${{\text{f}}_{\text{L}}}$ thì ${{\text{U}}_{\text{Lmax}}}$ và dòng điện trễ pha
hơn u góc $\text{ }\!\!\varphi\!\!\text{ }$. Giá trị $\text{
}\!\!\varphi\!\!\text{ }$ là
A. 0,668 rad B. 0,686 rad C. 0,686 rad D. 0,886 rad
Bài
24: Đặt vào hai đầu AB điện áp xoay chiều
u = $\text{U}\sqrt{\text{2}}$cos$\text{2 }\!\!\pi\!\!\text{ ft}$ V vào hai đầu
đoạn mạch AB theo thứ tự điện trở thuần, cuộn dây thuần cảm,tụ C mắc nối tiếp.
N là điểm giữa cuộn dây và tụ điện. Điều chỉnh $\text{ }\!\!\omega\!\!\text{ }$
để điện áp hiệu dụng trên tụ có giá trị cực đại, khi đó ${{\text{u}}_{\text{AN}}}$
lệch pha 1,2373 rad so với ${{\text{u}}_{\text{AB}}}$, công suất tiêu thụ khi đó
là 300 W. Khi điều chỉnh $\text{ }\!\!\omega\!\!\text{ }$ để công suất tiêu thụ
của mạch đạt giá trị cực đại thì giá trị đó bằng:
A. 300 W B. 4500 W C. 250 W D. 525 W.
Bài
25: Đoạn mạch xoay chiều AB có RLC nối tiếp,
cuộn dây thuần cảm với $\text{C}{{\text{R}}^{\text{2}}}$ < 2L, điện áp hai đầu
đoạn mạch là ${{\text{u}}_{\text{AB}}}$ = $\text{U}\sqrt{\text{2}}$cos$\text{
}\!\!\omega\!\!\text{ t}$ V, U ổn định và $\text{ }\!\!\omega\!\!\text{ }$ thay
đổi. Khi $\text{ }\!\!\omega\!\!\text{ }$ = ${{\text{ }\!\!\omega\!\!\text{
}}_{\text{C}}}$ thì điện áp hai đầu tụ C cực đại, khi đó điện áp tức hai đầu đoạn
mạch AN (gồm RL) và AB lệch pha nhau là $\text{ }\!\!\alpha\!\!\text{ }$. Giá
trị nhỏ nhất của tan$\text{ }\!\!\alpha\!\!\text{ }$ là
A. $2\sqrt{2}$ B. $\frac{\sqrt{2}}{2}$ C. 2,5 D. $\sqrt{3}$
Bài
26: Cho mạch điện xoay chiều mắc nối tiếp
gồm các phần tử điện trở thuần R, cuộn dây thuần cảm có độ tự cảm L và tụ điện
có điện dung C. Mạch chỉ có tần số góc thay đổi được. Khi $\text{
}\!\!\omega\!\!\text{ }$ = ${{\text{ }\!\!\omega\!\!\text{ }}_{\text{1}}}$ = $\text{100
}\!\!\pi\!\!\text{ }$ rad/s thì điện áp hiệu dụng hai đầu cuộn cảm cực đại. Khi
$\text{ }\!\!\omega\!\!\text{ }$ = ${{\text{ }\!\!\omega\!\!\text{
}}_{\text{2}}}$ = 2${{\text{ }\!\!\omega\!\!\text{ }}_{\text{1}}}$ thì điện áp
hai đầu tụ điện cực đại. Biết khi $\text{ }\!\!\omega\!\!\text{ }$ = ${{\text{
}\!\!\omega\!\!\text{ }}_{\text{1}}}$ thì ${{\text{Z}}_{\text{L}}}$ + 3${{\text{Z}}_{\text{C}}}$
= 400 $\Omega $. Giá trị L bằng
A. $\frac{\text{4}}{\text{7
}\!\!\pi\!\!\text{ }}$ H B. $\frac{\text{4}}{\text{3
}\!\!\pi\!\!\text{ }}$ H C. $\frac{\text{3}}{\text{4
}\!\!\pi\!\!\text{ }}$ H D. $\frac{\text{7}}{\text{4
}\!\!\pi\!\!\text{ }}$ H
Bài
27: Mạch điện AB gồm R, L, C nối tiếp, ${{\text{u}}_{\text{AB}}}$
= $\text{U}\sqrt{\text{2}}$cos$\text{ }\!\!\omega\!\!\text{ t}$ V, U ổn định và
$\text{ }\!\!\omega\!\!\text{ }$ thay đổi. Giá trị hiệu dụng của điện áp ở hai
đầu các phần tử lần lượt là ${{\text{U}}_{\text{R}}}$, ${{\text{U}}_{\text{L}}}$,
${{\text{U}}_{\text{C}}}$. Cho $\text{ }\!\!\omega\!\!\text{ }$ tăng dần từ 0 đến
$\infty $ thì thứ thự đạt cực đại của các điện áp trên là
A. ${{\text{U}}_{\text{C}}}$, ${{\text{U}}_{\text{R}}}$,
${{\text{U}}_{\text{L}}}$ B. ${{\text{U}}_{\text{C}}}$, ${{\text{U}}_{\text{L}}}$, ${{\text{U}}_{\text{C}}}$
C. ${{\text{U}}_{\text{L}}}$,
${{\text{U}}_{\text{R}}}$, ${{\text{U}}_{\text{C}}}$ D. ${{\text{U}}_{\text{R}}}$, ${{\text{U}}_{\text{L}}}$,
${{\text{U}}_{\text{C}}}$
*
Đáp án
|
1 B |
2 D |
3 A |
4 A |
5 B |
6 C |
7 B |
8 B |
9 A |
10 B |
|
11 D |
12 A |
13 A |
14 C |
15 A |
16 A |
17 C |
18 D |
19 C |
20 A |
|
21 C |
22 A |
23 D |
24 D |
25 D |
26 A |
27 A |
|
|
. |







