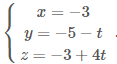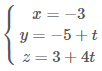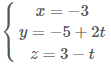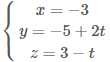Các xác định nhanh Phương Trình Hình Chiếu Vuông Góc Của Đường Thẳng Lên Mặt Phẳng trong không gian Oxyz

(1). Phương trình hình chiếu vuông góc của $d$ lên $(P),$ với $d$ cắt $(P).$

Gọi $Q$ là mặt phẳng chứa $d$ và $Q\bot (P),$ do đó $\Delta =(P)\cap (Q)$ và

$\overrightarrow{{{u}_{\Delta }}}=\left[ \overrightarrow{{{n}_{P}}},\overrightarrow{{{n}_{Q}}} \right]=\left[ \overrightarrow{{{n}_{P}}},\left[ \overrightarrow{{{u}_{d}}},\overrightarrow{{{n}_{P}}} \right] \right],$ tìm một điểm thuộc $\Delta $ là $A=d\cap (P).$

(2). Nếu đường thẳng $d//(P),$ thì $\overrightarrow{{{u}_{\Delta }}}=\overrightarrow{{{u}_{d}}}$ và điểm $B\in \Delta $ là hình chiếu của điểm $A\in d$ lên mặt phẳng $(P).$

Ví dụ 1.Trong không gian với hệ toạ độ $Oxyz,$ cho đường thẳng $d:\frac{x-1}{2}=\frac{y+5}{-1}=\frac{z-3}{4}.$ Phương trình nào dưới đây là phương trình của hình chiếu vuông góc của $d$ lên mặt phẳng $x+3=0?$

Gọi $Q$ là mặt phẳng chứa $d$ và $Q\bot (P),$ do đó $\Delta =(P)\cap (Q)$ và

$\overrightarrow{{{u}_{\Delta }}}=\left[ \overrightarrow{{{n}_{P}}},\overrightarrow{{{n}_{Q}}} \right]=\left[ \overrightarrow{{{n}_{P}}},\left[ \overrightarrow{{{u}_{d}}},\overrightarrow{{{n}_{P}}} \right] \right]=(0;1;-4)$ và dễ có $d\cap (P)=A(-3;-3;-5)\in \Delta ,$

Vậy $d\cap (P)=A(-3;-3;-5)\in \Delta ,$ đối chiếu đáp án nhận D.

Bài tập tự luyện:

Trong không gian với hệ toạ độ $Oxyz,$ cho mặt phẳng $(P):x+y-3z-3=0$ và đường thẳng $d:\frac{x-1}{2}=\frac{y}{-3}=\frac{z+2}{1}.$ Gọi ${d}'$ là hình chiếu vuông góc của $d$ lên mặt phẳng $(P).$ Tìm một véctơ chỉ phương của ${d}'.$

Bài viết gợi ý: