CẤU TẠO HẠT NHÂN VÀ NĂNG LƯƠNG LIÊN KẾT HẠT NHÂN
I .TÓM TẮT LÍ THUYẾT :
1. Cấu tạo hạt nhân :
a) Hạt nhân nguyên tử được cấu tạo từ các nuclôn gồm :
+ prôtôn ( p ) có mp = \[1,{{67262.10}^{-27}}\] kg , điện tích : +e .
+ nơtrôn (n ) có mn =\[1,{{67493.10}^{-27}}\] kg , không mang điện tích .
- Kí hiệu hạt nhân : \[{}_{Z}^{A}X\] . Trong đó :
+Z là số hiệu nguyên tử , chính là số thứ tự trong bảng HTTH .
+ A gọi là số khối , là tổng số các nuclon trong hạt nhân .
\[\Rightarrow \] số nơtron = A – Z .
b) Kích thước hạt nhân :
Nếu coi hạt nhân nguyên tử là một khối cầu bán kính R thì ta có sự phụ thuộc giữa R và số khối A là :
R = 1,2.\[{{10}^{-15}}.{{A}^{\frac{1}{3}}}\] (m) .
2. Đồng vị : là những nguyên tử mà hạt nhân chứa cùng số proton nhưng có số nơtron khác nhau .
- Các đồng vị phóng xạ được chia làm hai loại :
+ đồng vị bền : trong thiên nhiên có khoảng 300 đồng vị loại này .
+ đồng vị phóng xạ ( không bền) : có khoảng vài nghìn đồng vị phóng xạ tự nhiên và nhân tạo .
3. Đơn vị khối lượng nguyên tử :
- Kí hiệu là u và có trị số bằng 1 / 12 khối lượng của đồng vị \[{}_{6}^{12}C\]. Khi đó : 1u = \[1,{{66055.10}^{-27}}\]kg .
Từ hệ thức Anh-xtanh : E= mc2 \[\Rightarrow \] 1u = 931,5 MeV /c2
4. Độ hụt khối và năng lượng liên kết :
a) Lực hạt nhân : là lực tương tác giữa các nuclon trong hạt nhân. Lực này có đặc điểm là lực hút , có bán kính tác dụng rất nhỏ - cỡ 10-15 m và có cường độ rẩt lớn nên còn gọi là lự tương tác mạnh .
b) Độ hụt khối : là hiệu số khối lượng giữa khối lượng hạt nhân và tổng khối lượng các nuclon cấu tạo nên hạt nhân đó .
Ta có công thức tính độ hụt khối của hạt nhân : Δm = ∑ mp + ∑ mn ─ m ( chú ý đơn vị là u ).
c) Năng lượng liên kết :
- Từ hệ thức Anh-xtanh : E = mc2 . Ta thấy 1 phần khối lượng của các hạt nuclon đã chuyển thành năng lượng liên kết các hạt nhân trong nguyên tử với nhau ( vì thế nên m < m0 ) : năng lượng đó được gọi là năng lượng liên kết của hạt nhân và có trị số : Wlk = Δm.c2 .
Năng lượng liên kết càng lớn thì lực liên kết giữa các nuclôn càng mạnh .
─ Để đặc trưng cho độ bền vững của hạt nhân ta có đại lượng năng lượng liên kết riêng là : \[\frac{{{W}_{lk}}}{A}\]. Hạt
nhân có năng lượng liên kết riêng càng lớn thì càng bền vững
II . PHƯƠNG PHÁP GIẢI BÀI TẬP .
Loại 1 : Tìm độ hụt khối và năng lượng liên kết của hạt nhân :
a) Độ hụt khối : của một hạt nhân \[{}_{Z}^{A}X\]
Δm = ∑ mp + ∑ mn ─ m = Zmp + (A – Z)mn ─ m . (1.1)
b) Năng lượng liên kết :
- tính độ hụt khối và suy ra năng lượng liên kết của hạt nhân : Wlk = Δm.c2 = Δm.931 (MeV) (1.2)
Chú ý : thường thì đề bài cho 1u = 931 MeV/c2 nhưng nếu đề không cho thì cứ lấy giá trị chuẩn ( theo cách lấy của đề thi đại học ) là 1u = 931,5 MeV/c2 .
có thể đề yêu cầu tính năng lượng cần thiết để tách ( năng lượng toả ra) của N hạt nhân \[{}_{Z}^{A}X\] . Chính là năng lượng liên kết của 1 hạt nhân đó
Và N hạt nhân thì có năng lượng là : E = N.Wlk ( MeV)
Ví dụ 1: [07A] Cho mC = 12 u, mp= 1.00728u, mn = 1,00867u , 1u = 1.66058.10-27 kg , 1eV = 1,6.10-19 J, c = 3.10-8 m/s. Năng lượng tối thiểu để tách hạt nhân \[{}_{6}^{12}C\] thành các nuclon riêng biệt bằng :
A. 8,94 MeV B. 44,7 MeV C. 89,4 MeV D. 72,7 MeV
Giải:
Ta phải tính 1u bằng bao nhiêu MeV ?
Năng lượng của 1u ( tính theo đơn vị J ) bằng : 1u = mc2/c2 = (1,66058.10 – 27 .9.1016 )/ c2
= 1,494522.10-10 J / c2.
Mà 1,6.10 – 13 J thì bằng 1 MeV .
Suy ra 1,494522.10-10 J bằng \[\Rightarrow \] \[\frac{1,{{494522.10}^{-10}}}{1,{{6.10}^{-13}}}=934,07\] MeV
Vậy 1u = 934,07 MeV/ c2
Năng lượng cần thiết để tách hạt nhân \[{}_{6}^{12}C\]thành các nuclôn riêng biệt chính là năng lượng liên kết của hạt nhân \[{}_{6}^{12}C\] :
E = Wlk = Δm.c2 = (6.mp +6.mn – mC).c2 = (6.1.00728 +6.1,00867 – 12).934,07 = 8489,4 MeV Đáp án : C
Ví dụ 2: Xem ban đầu hạt nhân \[{}_{6}^{12}\]C đứng yên .Cho bieát mC =12,0000u ; mα = 4,0015u. Năng lượng tối thiểu để tách hạt nhân \[{}_{6}^{12}\]C thành 3 hạt nhân α là?
A. 6,7.10 – 13 J B. 7,7.10 – 13 J C. 8,2.10 – 13 J D. 5,6.10 – 13 J
Giải:
- Năng lượng tối thiểu để tách hạt nhân 12C thành 3 hạt nhân α chính là năng lượng cần cung cấp cho
do độ hụt khối của 1C tạo 3α.Năng lượng đó bằng:
Q = (mC – mα ).c2 = – 0,0045u.c2 = – 4,1895 MeV = – 6,7.10–13 J
Dấu trừ chứng tỏ phản ứng cần cung cấp năng lượng .
 Chọn đáp án A
Chọn đáp án A
Ví dụ 3: Cho phản ứng phân hạch Uran 235 : \[{}_{0}^{1}\]n +235\[{}_{92}^{235}\]U → \[{}_{56}^{144}\]Ba + \[{}_{36}^{89}\]Kr + 3\[{}_{0}^{1}\]n + 200 MeV. Bieát 1u = 931 MeV/c2. Năng lượng hụt khối của phản ứng là? A.0,3148u B.0,2248u C. 0,2848u D. 0,2148u
Giải:
Ta có năng lượng toả ra của phản ứng trên là : Q = (m0 – m ).c2 = Δm.c2 = 200 MeV
Suy ra độ hụt khối của phản ứng bằng:
Δm = \[\frac{Q}{931}=\frac{200}{931}=0,2148\] u
\[\Rightarrow \] Chọn đáp án D
Loại 2 : Tính năng lượng liên kết riêng và so sánh tính bền vững của các hạt nhân.
- Ta tính năng lượng liên kết riệng bằng : \[\frac{{{W}_{lk}}}{A}\] MeV/nuclon.
- Rồi so sánh năng lượng liên kết riêng của các hạt nhân với nhau : hạt nhân có năng lượng liên kết riêng càng lớn thì càng bền vững .
Chú ý : hạt nhân có số khối từ 50 – 70 trong bảng HTTH thường bền hơn các nguyên tử của các hạt nhân còn lại
Ví dụ 1:[08A] Hạt nhân \[{}_{4}^{10}Be\]có khối lượng 10,0135u. Khối lượng của nơtrôn (nơtron) mn = 1,0087u, khối lượng của prôtôn (prôton) mP = 1,0073u, 1u = 931 MeV/c2. Năng lượng liên kết riêng của hạt nhân 10 là \[{}_{4}^{10}Be\]
A. 0,6321 MeV. B. 63,2152 MeV. C. 6,3215 MeV. D. 632,1531 MeV
Giải:
Năng lượng liên kết của hạt nhân \[{}_{4}^{10}Be\] là
Wlk = Δm.c2 = (4.mP +6.mn – mBe).c2 = 0,0679.c2 = 63,215 MeV
Suy ra năng lượng liên kết riêng của hạt nhân \[{}_{4}^{10}Be\] là : \[\frac{{{W}_{lk}}}{A}=\frac{63,125}{10}=6,3215\]MeV/nuclôn.Chọn đáp án : C
Ví dụ 2: Tính năng lượng liên kết hạt nhân Đơtêri \[{}_{1}^{2}D\]? Cho mp = 1,0073u, mn = 1,0087u, mD = 2,0136u;
1u = 931 MeV/c2.
A) 2,431 MeV. B) 1,122 MeV. C) 1,243 MeV. D)2,234MeV
Giải:
Độ hụt khối của hạt nhân D
Δm = ∑ mp + ∑ mn ─ mD = 1.mp +1.mn – mD = 0,0024 u
Năng lượng liên kết cảu hạt nhân D là
Wlk = Δm.c2 = 0,0024.uc2 = 2,234 MeV
\[\Rightarrow \] Chọn đáp án D
Ví dụ 3 : Cho biết mα = 4,0015u; \[{{m}_{O}}=15,999\]u; \[{{m}_{p}}=1,007276u\], \[{{m}_{n}}=1,008667u\]. Hãy sắp xếp các hạt nhân \[{}_{2}^{4}He\], \[{}_{6}^{12}C\], \[{}_{8}^{16}O\] theo thứ tự tăng dần độ bền vững :
Câu trả lời đúng là:
A. \[{}_{6}^{12}C\],\[{}_{2}^{4}He,\]\[{}_{8}^{16}O\].
B. \[{}_{6}^{12}C\], \[{}_{8}^{16}O\], \[{}_{2}^{4}He,\]
C. \[{}_{2}^{4}He,\] \[{}_{6}^{12}C\], \[{}_{8}^{16}O\].
D. \[{}_{2}^{4}He,\]\[{}_{8}^{16}O\],\[{}_{6}^{12}C\].
Giải:
- Ta thấy đề bài không cho khối lượng của 12C nhưng chú ý vì ở đây dùng đơn vị u, mà theo định nghĩa đon vị u bằng 1/12 khối lượng đồng vị 12C \[\Rightarrow \] do đó có thể lấy khối lượng 12C là 12 u.
Suy ra năng lượng liên kết riêng của từng hạt nhân là
He : Wlk = (2.mp + 2.mn – m α )c2 = 28,289366 MeV \[\Rightarrow \] Wlk riêng = 7,0723 MeV / nuclon.
C : Wlk = (6.mp + 6.mn – mC )c2 = 89,057598 MeV \[\Rightarrow \] Wlkriêng = 7,4215 MeV/ nuclon.
O : Wlk = (8.mp + 8.mn – mO )c2 = 119,674464 meV \[\Rightarrow \] Wlk riêng = 7,4797 MeV/ nuclon.
Hạt nhân có năng lượng liên kết riêng càng lớn thì càng bền vững. Vậy chiều bền vững hạt nhân tăng dần là : He < C < O.
\[\Rightarrow \] Chọn đáp án C
Loại 3 : Tính số hạt nhân nguyên tử và suy ra số nơtron, proton có trong lượng chất hạt nhân .
- Cho khối lượng m hoặc số mol của hạt nhân\[{}_{Z}^{A}X\] . Tìm số hạt p , n có trong mẫu hạt nhân đó .
Nếu có khối lượng m suy ra số hạt hạt nhân X là : N = \[\frac{m}{A}.{{N}_{A}}\] (hạt) .
Nếu có số mol suy ra số hạt hạt nhân X là : N = n.NA (hạt) . với NA = \[6,{{022.10}^{-23}}mo{{l}^{-1}}\]
Khi đó : 1 hạt hạt nhân X có Z hạt p và (A – Z ) hạt n . Do đó trong N hạt hạt nhân X có :
N.Z hạt p
(A-Z). N hạt n
Ví dụ 1: [07A] Biết số Avôgađrô là 6,02.10 23 mol-1, khối lượng mol của hạt nhân urani \[{}_{92}^{238}U\] là 238 gam / mol. Số nơtron trong 119 gam urani \[{}_{92}^{238}U\]là :
A. \[2,{{2.10}^{25}}\] hạt B.\[1,{{2.10}^{25}}\] hạt
C \[8,{{8.10}^{25}}\] hạt D. \[4,{{4.10}^{25}}\] hạt
Giải:
- Số hạt nhân có trong 119 gam urani \[{}_{92}^{238}U\]là :
N = \[\frac{m}{A}.{{N}_{A}}\] \[=\frac{119}{238}.6,{{02.10}^{23}}={{3.01.10}^{23}}\] hạt
- Suy ra số hạt nơtron có trong N hạt nhân urani \[{}_{92}^{238}U\] là :
(A-Z). N = ( 238 – 92 ).3,01.1023 = 4,4.1025 hạt
\[\Rightarrow \] Đáp án : D
II.PHÓNG XẠ
I. TÓM TẮT LÍ THUYẾT
1. Định nghĩa và tính chất phóng xạ :
- Phóng xạ là hiện tượng một hạt nhân không bền vững tự phát phân rã, phát ra các tia phóng xạ và biến đổi thành hạt nhân khác gọi là hiện tượng phóng xạ .
- Đặc điểm của hiện tượng phóng xạ :
+ quá trình phân rã phóng xạ chính là quá trình dẫn đến sự biến đổi hạt nhân.
+quá trình phân rã phóng xạ chỉ do các nguyên nhân bên trong gây ra và hoàn toàn không chịu tác động của các yếu tố thuộc môi trường ngoài .
2. Các loại tia phóng xạ :
Quá trình phân rã phóng xạ phát ra gồm 3 loại tia phóng xạ : tia α , tia β và tia γ
Các tia phóng xạ là tia không nhìn thấy được và có tính chất là : kích thích một số phản ứng hoá học, ion hoá không khí, làm đen kính ảnh, xuyên thấu lớp vật chất mỏng, phá huỷ tế bào…
a) Tia α :
- bản chất là chùm hạt nhân nguyên tử heli\[{}_{2}^{4}He\]
- tính chất : bị lệch về phía bản âm của điện trường, có vận tốc khoảng 2.10 -7 m/s. Có tính ion hoá mạnh nên mất năng lượng rất nhanh trên đường đi, khả năng đâm xuyên yếu.
b) Tia β :
- gồm 2 loại và có đặc điểm chung là phóng ra với tốc độ rất lớn xấp xỉ tốc độ ánh sáng . Làm ion hoá môi trường nhưng yếu hơn tia α nên truyền đi với quãng đường dài hơn, khả năng đâm xuyên mạnh hơn tia α ( có thể đâm xuyên qua lá nhôm dày cỡ mm).
- tia β- : là chùm các hạt e- ( là loại phóng xạ phổ biến hơn β+ ) và bị lệch về bản dương của điện trường.
- tia β+ : là chùm các hạt pozitron e+ có điện tích +e ( là phản hạt của electron – sẽ đề cập rõ ở chương các loại hạt sơ cấp ) nên bị lệch về phía bản âm của điện trường .
c) Tia γ :
- là sóng điện từ có bước sóng cực ngắn < 10 -11 m ( chính là chùm phôtôn mang có năng lượng cao ).
- tính chất : không bị lệch trong điện trường , có khả năng đâm xuyên mạnh hơn nhiều so với tia α , β .
Trong phân rã α , β tạo hạt nhân con ở trạng thái kích thích và hạt nhân con có thể phóng xạ ra tia γ để trở về trạng thái cơ bản.
3. Định luật phóng xạ:
a) Định luật phóng xạ :
- Trong quá trình phân rã , số hạt nhân phóng xạ giảm theo thời gian theo định luật hàm số mũ.
- Các hàm biễu diễn quá trình phân rã phóng xạ hạt nhân theo thời theo thời gian t :
+ theo khối lượng : m = \[{{m}_{0}}{{.2}^{-\frac{t}{T}}}={{m}_{0}}.{{e}^{-\lambda .t}}\].
+ theo số hạt hạt nhân nguyên tử : N = \[{{N}_{0}}{{.2}^{-\frac{t}{T}}}={{N}_{0}}.{{e}^{-\lambda .t}}\]
Trong đó : m0 ,m là khối lượng hạt nhân nguyên tử và N0, N là số hạt hạt nhân nguyên tử .
T là chu kì bán rã .
\[\lambda =\frac{\ln 2}{T}\] : là hằng số phóng xạ .
b) Độ phóng xạ :
- là đại lượng đặc trưng cho tính phóng xạ mạnh hay yếu của một lượng chất phóng xạ , được xác định là số phân rã trong một giây. Đặc trưng cho tốc độ phân rã .
- Kí hiệu là H và có đơn vị là Becơren (Bq) , với 1 Bq = 1 phân rã /s.
-Xác định độ phóng xạ : \[H=\lambda .N={{H}_{0}}.{{e}^{-\lambda .t}}\] , trong đó H0 = λ.N0 : được gọi là độ phóng xạ ban đầu của hạt nhân .
4. Đồng vị phóng xạ và ứng dụng :
a) Đồng vị phóng xạ : gồm có đồng vị phóng xạ tự nhiên và nhân tạo
- các đồng vị phóng xạ của một nguyên tố hoá học có cùng tính chất hoá học như đồng vị bền của nguyên tố đó.
b) Ứng dụng:
- trong khảo cổ học dùng đồng vị \[{}_{6}^{14}C\]có T = 5730 năm để xác định tuổi mẫu vật.
- trong y-sinh học : phương pháp đánh dấu nguyên tử và phẩu thuật chiếu xạ.
II. PHƯƠNG PHÁP GIẢI BÀI TẬP
Loại 1: Xác định lượng chất còn lại:
- Cho m0 hay N0 và T. Tìm khối lượng (số hạt nhân nguyên tử ) con lại sau thời gian t ?
Tính số hạt hạt nhân nguyên tử \[{}_{Z}^{A}X\] trong m (g) vật chất. \[{{N}_{0}}=\frac{{{m}_{0}}.{{N}_{A}}}{A}\] hạt.
Khối lượng còn lại của X sau thời gian t : m =\[{{m}_{0}}{{.2}^{-\frac{t}{T}}}={{m}_{0}}.{{e}^{-\lambda .t}}\]. (2.1)
Số hạt nhân X còn lại sau thời gian t : N = \[{{N}_{0}}{{.2}^{-\frac{t}{T}}}={{N}_{0}}.{{e}^{-\lambda .t}}\]. (2.2)
Chú ý: là t và T phải đưa về cùng đơn vị . Đối với khối lượng m thì không cần đổi đơn vị và ta cứ tính rồi lấy đơn vị của m theo m0 như đề bài.
Ví dụ 1:[08A] Một chất phóng xạ có chu kỳ bán rã là 3,8 ngày. Sau thời gian 11,4 ngày thì độ phóng xạ (hoạt độ phóng xạ) của lượng chất phóng xạ còn lại bằng bao nhiêu phần trăm so với độ phóng xạ của lượng chất phóng xạ ban đầu?
A. 25%. B. 75%. C. 12,5%. D. 87,5%
Giải:
- Ta có : T = 3,8 ngày ; t = 11,4 = 3T ngày . Do đó ta đưa về hàm mũ hai để giải nhanh như sau :
\[m={{m}_{0}}{{.2}^{-\frac{t}{T}}}\Leftrightarrow \frac{m}{{{m}_{0}}}={{2}^{-\frac{t}{T}}}\]\[\Leftrightarrow \]\[\frac{m}{{{m}_{0}}}={{2}^{-3}}=\frac{1}{8}\] = 12,5%
\[\Rightarrow \] Chọn đáp án : C
Ví dụ 2:[09A] Một chất phóng xạ ban đầu có N0 hạt nhân. Sau 1 năm, còn lại một phần ba số hạt nhân ban đầu chưa phân rã. Sau 1 năm nữa, số hạt nhân còn lại chưa phân rã của chất phóng xạ đó là
A. N0 /6 B. N0 /16. C. N0 /9. D. N0 /4.
Giải
- Ta có : t = 1năm thì số hạt nhân chưa phân rã (còn lại ) là : \[\frac{N}{{{N}_{0}}}=\frac{1}{{{2}^{\frac{t}{T}}}}=\frac{1}{3}\]
- Sau 1năm nữa tức là t’ = 2t năm thì số hạt nhân còn lại chưa phân rã là :
\[\frac{N}{{{N}_{0}}}=\frac{1}{{{2}^{\frac{t'}{T}}}}=\frac{1}{{{2}^{\frac{2t}{T}}}}\] \[\Leftrightarrow \]\[\frac{N}{{{N}_{0}}}=\left( \frac{1}{{{2}^{\frac{t}{T}}}} \right)={{\left( \frac{1}{3} \right)}^{2}}=\frac{1}{9}\].
\[\Rightarrow \] Chọn đáp án : C
Loại 2: Xác định lượng chất đã bị phân rã :
- Cho khối lượng hạt nhân ban đầu ( hoặc số hạt nhân ban đầu N0 ) và T . Tìm lượng hạt nhân đã bị phân rã trong thời gian t ?
Khối lượng hạt nhân bị phân rã : Δm = \[{{m}_{0}}-m={{m}_{0}}(1-{{2}^{-\frac{t}{T}}})={{m}_{0}}(1-{{e}^{-\lambda .t}})\] (2.3)
Số hạt nhân bị phân rã là : ΔN = \[{{N}_{0}}-N={{N}_{0}}(1-{{2}^{-\frac{t}{T}}})={{N}_{0}}(1-{{e}^{-\lambda .t}})\] (2.4)
Chú ý : là không được áp dụng định luật bảo toàn khối lươngj như trong phản ứng hoá học.
A -> B + C . mA ≠ mB + mC
Ví dụ 1:Tính số hạt nhân bị phân rã sau 1s trong 1g Rađi \[{}^{226}\]Ra . Cho biết chu kỳ bán rã của \[{}^{226}\]Ra là 1580 năm. Số Avôgađrô là NA = 6,02.1023 mol-1.
A). 3,55.1010 hạt. B). 3,40.1010 hạt. C). 3,75.1010 hạt. D).3,70.1010 hạt.
Giải
- Số hạt nhân nguyên tử có trong 1 gam 226Ra là : N0 = \[\frac{m}{A}.{{N}_{A}}=\frac{1}{226}.6,{{022.10}^{23}}=2,{{6646.10}^{21}}\] hạt .
- Suy ra số hạt nhân nguyên tử Ra phân rã sau 1 s là :
\[\Delta N={{N}_{0}}(1-{{2}^{-\frac{t}{T}}})=2,{{6646.10}^{21}}\left( 1-{{2}^{-\frac{1}{1580.365.86400}}} \right)=3,{{70.10}^{10}}\] hạt .
\[\Rightarrow \] Chọn đáp án D
Loại 3 : Xác định khối lượng của hạt nhân con :
- Cho phân rã : \[{}_{Z}^{A}X\to {}_{Z'}^{B}Y\]+ tia phóng xạ . Biết m0 , T của hạt nhân mẹ.
Ta có : 1 hạt nhân phóng xạ thì sẽ có 1 hạt nhân con tao thành. Do đó ΔNX (phóng xạ) = NY (tạo thành)
Mà \[\Delta {{N}_{X}}=\frac{\Delta {{m}_{X}}}{A}.{{N}_{A}}\] ( NA là số Avôgađrô ) .
Suy ra : \[{{m}_{Y}}=n.B=\frac{{{N}_{Y}}}{{{N}_{A}}}.B=\frac{\frac{\Delta {{m}_{X}}}{A}.{{N}_{A}}}{{{N}_{A}}}.B=\frac{\Delta {{m}_{X}}.B}{A}\] \[\Leftrightarrow \] \[{{m}_{Y}}=\frac{\Delta {{m}_{X}}.B}{A}\].
Tổng quát : mcon = \[\frac{\Delta {{m}_{me}}.{{A}_{con}}}{{{A}_{me}}}\] (2.5)
Ví dụ 1:[08A] Hạt nhân \[{}_{A.1}^{Z.1}X\] phóng xạ và biến thành một hạt nhân \[{}_{A.2}^{Z.2}Y\] bền. Coi khối lượng của hạt nhân X, Y bằng số khối của chúng tính theo đơn vị u. Biết chất phóng xạ \[{}_{A.1}^{Z{{.1}_{1}}}X\] có chu kì bán rã là T. Ban đầu có một khối lượng chất \[{}_{A.1}^{Z{{.1}_{1}}}X\], sau 2 chu kì bán rã thì tỉ số giữa khối lượng của chất Y và khối lượng của chất X là :
A. \[4\frac{{{A}_{1}}}{{{A}_{2}}}\] B. \[4\frac{{{A}_{2}}}{{{A}_{1}}}\]
C. \[3\frac{{{A}_{1}}}{{{A}_{2}}}\] D. \[3\frac{{{A}_{2}}}{{{A}_{1}}}\]
Giải
- Xem phản ứng trên như sau : X → Y + tia phóng xạ .
Khi đó X là hạt nhân mẹ và Y là hạt nhân con tao thành. Lúc này bài toán trở thành tìm mối liên hệ giữa X và hạt nhân con Y :
- Ta có khối lượng của hạt nhân X sau 2 chu kì ( t = 2T ):
+ m =\[{{m}_{0}}{{.2}^{-\frac{t}{T}}}={{m}_{0}}{{.2}^{-2}}=\frac{{{m}_{0}}}{4}\] .
- Khối lượng của hạt nhân con Y tạo thành sau 2 chu kì là :
mY = \[\frac{\Delta {{m}_{X}}.{{A}_{Y}}}{{{A}_{X}}}\] \[\Leftrightarrow \] mY = \[\frac{{{m}_{0}}(1-{{2}^{-2}}).{{A}_{2}}}{{{A}_{1}}}=\frac{{{m}_{0}}(1-\frac{1}{4}).{{A}_{2}}}{{{A}_{1}}}=\frac{3{{m}_{0}}{{A}_{2}}}{4{{A}_{1}}}\]
- Khi đó, tỉ lệ giữa khối lượng của hạt nhân Y và hạt nhân X là :
+ \[\frac{{{m}_{Y}}}{{{m}_{X}}}=\frac{\frac{3{{m}_{0}}}{4}\times \frac{{{A}_{2}}}{{{A}_{1}}}}{\frac{{{m}_{0}}}{4}}=\frac{3{{A}_{2}}}{{{A}_{1}}}\] \[\Rightarrow \] Chọn phương án D
Ví dụ 2: \[{}_{11}^{24}\] Na là chất phóng xạ β- tạo thành hạt nhân magiê \[{}_{12}^{24}\]Mg. Ban đầu có 12gam Na và chu kì bán rã là 15 giờ. Sau 45 h thì khối lượng Mg tạo thành là :
A. 10,5g B. 5,16 g C. 51,6g D. 0,516g
Giải
Nhận xét : t = 3.T nên ta dùng hàm mũ 2 để giải cho nhanh bài toán :
- khối lượng Na bị phân rã sau 45 = 3T giờ : Δm = \[={{m}_{0}}(1-{{2}^{-\frac{t}{T}}})=12(1-{{2}^{-\frac{1}{3}}})\]
\[\Leftrightarrow \]Δm = 10,5 g .
Suy ra khối lượng của mg tạo thành : mcon = \[\frac{\Delta {{m}_{me}}.{{A}_{con}}}{{{A}_{me}}}=\frac{10,5}{24}.24=10,5\]gam.
\[\Rightarrow \] Chọn đáp án A
Loại 4: Xác định độ phóng xạ của hạt nhân :
- Cho m0, T . Tìm độ phóng xạ của hạt nhân sau thời gian t ?
+ phải đưa khối lượng ban đầu về số hạt nhân ban đầu : \[{{N}_{0}}=\frac{{{m}_{0}}.{{N}_{A}}}{A}\] hạt .
+ đưa chu kì về đơn vị giây .
+ tính độ phóng xạ ban đầu : H0 = λ.N0 =\[\frac{\ln 2}{T}.{{N}_{0}}\] (Bq). (2.6)
+ tính độ phóng xạ sau thời gian t : \[H=\lambda .N=\lambda .{{N}_{0}}.{{e}^{-\lambda .t}}={{H}_{0}}.{{e}^{-\lambda .t}}\] (Bq). (2.7)
Chú ý: + ngoài đơn vị Bq , độ phóng xạ còn có đơn vị tính khác là Curi (Ci) , với 1Ci = 3,7.1010 Bq.
+ khi tính độ phóng xạ phải đổi T về s và nên lưu số này vào máy tính để tính nhanh trắc nghiệm :
1năm = 31,536.10 6 s .
Ví dụ 1:[09A] Lấy chu kì bán rã của pôlôni \[{}_{84}^{210}Po\] là 138 ngày và NA = 6,02.1023 mol-1. Độ phóng xạ của 42 mg pôlôni là
A. 7.1010 Bq. B. 7.1014 Bq. C. 7.1012 Bq. D. 7.109 Bq.
Giải
- Số hạt nhân nguyên tử \[{}_{84}^{210}Po\] có trong 42 mg là : \[{{N}_{0}}=\frac{{{m}_{0}}.{{N}_{A}}}{A}=\frac{{{42.10}^{-3}}.6,{{02.10}^{23}}}{210}=1,204.10{}^{20}\] hạt .
Độ phóng xạ của 42 mg pôlôni là : H0 = λ.N0 =\[\frac{\ln 2}{T}.{{N}_{0}}\] \[\Leftrightarrow \]H0 = \[\frac{\ln 2}{138.86400}.{{N}_{0}}\approx {{7.10}^{12}}\] Bq.
(Chú ý đổi về đúng đơn vị để tính vì bài này sai thường do không nhìn kĩ đơn vị khối lượng và chưa đổi T về giây ).
\[\Rightarrow \] Chọn đáp án C
Ví dụ 2: Sau mỗi giờ số nguyên tử của đồng vị phóng xạ cô ban giảm 3,8%. Hằng số phóng xạ cô ban
là:
- 0,783h-1 B. 0,239h-1 C. 0,0387h-1 D. 0,239h-1
Giải
- Số nguyên tử giảm mỗi giờ chính là lượng Co bị phóng xạ trong mỗi giờ , khi đó theo đề bài , ta có :
ΔN = \[{{N}_{0}}(1-{{e}^{-\lambda .t}})\] \[\Leftrightarrow \] \[1-{{e}^{-\lambda .t}}=\frac{\Delta N}{{{N}_{0}}}\] \[\Leftrightarrow \] \[{{e}^{-\lambda .t}}=1-\frac{\Delta N}{{{N}_{0}}}\] \[\Leftrightarrow \] \[\lambda =\frac{-\ln \left( 1-\frac{\Delta N}{{{N}_{0}}} \right)}{t}\].
- Hằng số phóng xạ của Co là : \[\lambda =\frac{-\ln \left( 1-\frac{\Delta N}{{{N}_{0}}} \right)}{t}=-\frac{\ln \left( 1-3,8% \right)}{1}\]= 0,0387 h-1 .
\[\Rightarrow \] Chọn đáp án D
Loại 5: Xác định thời gian phóng xạ , tuổi thọ vật chất.
- Cho m, m0 . Ta có : m \[={{m}_{0}}.{{e}^{-\lambda .t}}\] \[\Leftrightarrow \]\[-\lambda .t=\frac{-t\ln 2}{T}=\ln (\frac{m}{{{m}_{0}}})\] \[\Leftrightarrow \]\[t=\frac{-T}{\ln 2}.\ln \left( \frac{m}{{{m}_{0}}} \right)\] (2.7)
- Cho N, N0 . Lập luận tương tự , ta được :\[t=\frac{-T}{\ln 2}.\ln \left( \frac{N}{{{N}_{0}}} \right)\] (2.8)
- Cho H, H0 . Lập luận tương tự , ta được :\[t=\frac{-T}{\ln 2}.\ln \left( \frac{H}{{{H}_{0}}} \right)\] (2.9)
Chú ý :
-các đại lượng m – m0 , N - N0 , H – H0 phải cùng đơn vị . Và khi giải chỉ quan tâm có cùng đơn vị hay không chứ không cần phải đổi về đơn vị chuẩn để giải nhanh trắc nghiệm .
-các dạng đặc trưng :
+\[\frac{m}{{{m}_{0}}}\] = % lượng chất còn lại của hạt nhân sau khi phân rã trong thời gian t. Tương tự cho N/N0 và
H / H0 .
+ \[\frac{\Delta m}{{{m}_{0}}}\] = a% khối lượng hạt nhân đã bị phóng xạ . Tương tự cho ΔN/N0 và ΔH / H0 .Khi đó ta có thể suy ra khối lượng hạt nhân còn lại sau thời gian phân rã t là \[\frac{m}{{{m}_{0}}}\]= 100% - a% .
Ví dụ 1:[09A] Một đồng vị phóng xạ có chu kì bán rã T. Cứ sau một khoảng thời gian bằng bao nhiêu thì số hạt nhân bị phân rã trong khoảng thời gian đó bằng ba lần số hạt nhân còn lại của đồng vị ấy?
A. 2T. B. 3T. C. 0,5T. D. T.
Giải
- Sau thời gian phóng xạ t ( kể từ thời điểm ban đầu ) , ta có :
+ khối lượng hạt nhân còn lại : m \[={{m}_{0}}{{.2}^{-\frac{t}{T}}}\]
+ khối lượng hạt nhân bị phân rã : Δm = \[={{m}_{0}}\left( 1-{{2}^{-\frac{t}{T}}} \right)\].
- Theo đề , ta có : \[\frac{\Delta m}{m}=\frac{{{m}_{0}}(1-{{2}^{-\frac{t}{T}}})}{{{m}_{0}}{{.2}^{-\frac{t}{T}}}}=3\] \[\Leftrightarrow \]\[{{2}^{\frac{t}{T}}}-1=3\Leftrightarrow {{2}^{\frac{t}{T}}}=4\] \[\Leftrightarrow \] t = 2T.
Vậy cứ sau khoảng thời gian Δt = 2T thì khối lượng hạt nhân bị phóng xạ bằng 3 lần khối lượng hạt nhân còn lại .
\[\Rightarrow \] Chọn đáp án : A
Ví dụ 2: Một chất phóng xạ có chu kì bán rã là 360 giờ. Sau bao lâu thì khối lượng của nó chỉ còn 1/32 khối lượng ban đầu :
A. 75 ngày (24h) B. 11,25 giờ C. 11,25 ngày D. 480 ngày
Ví dụ 3: Độ phóng xạ của một tượng gỗ bằng 0,8 lần độ phóng xạ của mẫu gỗ cùng loại cùng khối lượng vừa mới chặt. Biết chu kì của 14C là 5600 năm. Tuổi của tượng gỗ đó là :
A. 1900 năm B. 2016 năm C. 1802 năm D. 1890 năm
Giải
- Đây là bài toán so sánh giữa độ phóng xạ do 14C phân rã trong vật cần xác định tuổi và vật đối chiếu .
- Theo đề ta có : \[\frac{H}{{{H}_{0}}}=0,8\].
- Áp dụng : từ công thức (2.9) ta được : \[t=\frac{-T}{\ln 2}.\ln \left( \frac{H}{{{H}_{0}}} \right)=\frac{-5600.\ln 0,8}{\ln 2}=1802\] năm .
\[\Rightarrow \] Chọn đáp án C
Loại 6: Xác định chu kì bán rã .
a) Cho m & m0 ( hoặc N & N0) :
- Biết sau thời gian t thì mẫu vật có tỉ lệ m/m0 ( hay N/N0 ) . Tìm chu kì bán rã của mẫu vật ?
Ta có : : m \[={{m}_{0}}.{{e}^{-\lambda .t}}\] \[\Leftrightarrow \]\[{{e}^{-\lambda .t}}=\frac{m}{{{m}_{0}}}\] \[\Leftrightarrow \]\[-\frac{t.\ln 2}{T}=\ln \left( \frac{m}{{{m}_{0}}} \right)\] \[\Leftrightarrow \]\[T=\frac{-t.\ln 2}{\ln \left( \frac{m}{{{m}_{0}}} \right)}\] (2.10)
Tương tự cho N , N0 : \[T=\frac{-t.\ln 2}{\ln \left( \frac{N}{{{N}_{0}}} \right)}\] (2.11)
- Có thể dùng công thức hàm mũ để đoán và giải nhanh với những câu có số liệu đẹp.
Nếu \[\frac{m}{{{m}_{0}}}\]= \[\frac{N}{{{N}_{0}}}\] = \[\frac{1}{{{2}^{n}}}\] (với n є N * ) \[\Rightarrow \] \[\frac{t}{T}=n.\Rightarrow T=\frac{t}{n}\]
b) Dùng máy đo xung phóng xạ phát ra :
- Một mẫu vật chất chứa phóng xạ. tại thời điểm t1 máy đo được H1 xung phóng xạ và sau đó 1 khoảng Δt tại t2 đo được H2 xung phóng xạ. Tìm chu kì bán rã của đồng vị phóng xạ đó là ?
Chọn thời điểm ban đầu tại t1. Khi đó : t0 ≡ t1 có H0 ≡ H1 và t ≡ t2 có H ≡ H2 .Suy ra được :
\[H={{H}_{0}}.{{e}^{-\lambda .t}}\] \[\Leftrightarrow \] \[{{e}^{-\lambda .t}}=\frac{H}{{{H}_{0}}}\] \[\Leftrightarrow \]\[T=\frac{-t.\ln 2}{\ln \left( \frac{H}{{{H}_{0}}} \right)}\] (2.12)
Ví dụ 1:[07A] Giả sử sau 3 giờ phóng xạ (kể từ thời điểm ban đầu ) số hạt nhân của một đồng vị phóng xạ còn lại bằng 25% số hạt nhân ban đầu. Chu kì bán rã của đồng vị phóng xạ đó bằng :
A. 1 giờ B. 1,5 giờ C. 0,5 giờ D. 2 giờ
Giải
- Ta có tỉ lệ : \[\frac{m}{{{m}_{0}}}\]= 25% = \[\frac{1}{4}=\frac{1}{{{2}^{2}}}\] mà \[\frac{m}{{{m}_{0}}}\]= \[\frac{1}{{{2}^{\frac{t}{T}}}}\] . Nên suy ra được : \[\frac{t}{T}\]= 2 .
Vậy chu lì bán rã của đồng vị phóng xạ đó bằng : T = \[\frac{t}{2}=\frac{3}{2}=1,5\] giờ.
\[\Rightarrow \] Chọn đáp án : B
Ví dụ 2: Độ phóng xạ của 3 mg \[{}_{27}^{60}\]Co là 3,41 Ci . Cho NA = 6,02.1023 mol-1, 1năm có 365 ngày. Tìm chu kì bán rã của Co là:
A.84 năm B. 5,24 năm C. 8,4 năm D. 4,8 năm
Giải
- Số hạt nhân nguyên tử của Na có trong 3 mg 60Co : \[{{N}_{0}}=\frac{m}{A}.{{N}_{A}}=\] 3,01.1019 hạt
Ta có : H0 = \[\frac{\ln 2}{T}.{{N}_{0}}\] \[\Leftrightarrow \] \[T=\ln 2.\frac{{{N}_{0}}}{{{H}_{0}}}\] .
Vậy chu kì bán rã của hạt nhân Co là : \[T=\ln 2.\frac{{{N}_{0}}}{{{H}_{0}}}=\frac{3,{{01.10}^{19}}.\ln 2}{3,41.3,{{7.10}^{10}}}\] \[\Leftrightarrow \]T = 5,24 năm .
\[\Rightarrow \] Chọn đáp án B
Ví dụ 3: \[{}_{11}^{24}\]Na là một chất phóng xạ . Sau thời gian 105 h thì độ phóng xạ của nó giảm đi 128 lần. Chu kì bán rã của \[{}_{11}^{24}\]Na là
A. 7,5h B. 15h C. 30h D. 3,75h
Giải
- Theo đề , ta có : \[\frac{H}{{{H}_{0}}}=\frac{1}{{{2}^{\frac{t}{T}}}}=\frac{1}{128}\] \[\Leftrightarrow \] \[\frac{t}{T}=7\] .
- Vậy chu kì bán rã bán rã của hạt nhân 23Na : T = \[\frac{t}{7}=15\] h .
\[\Rightarrow \] Chọn đáp án B
III.PHẢN ỨNG PHÂN HẠCH VÀ PHẢN ỨNG NHIỆT HẠCH
I. TÓM TẮT LÍ THUYẾT .
1. Phản ứng phân hạch :
a) Sự phân hạch :
- là sự vỡ một hạt nhân nặng thành hai hạt nhân nhẹ hơn và vài nơtron , sau khi hấp thụ một nơtron chậm.
- đặc điểm : mỗi phân hạch đều giải phóng ra năng lượng lớn.
b) Phản ứng phân hạch dây chuyền :
- Sau khi phân hạch một hạt nhân nặng (như U, Pu… ) thành các hạt nhân nhẹ hơn và kèm theo k hạt nơtron tiếp tục gây ra sự phân hạch cho các hạt nhân khác và số phân hạch tăng lên nhanh chóng : chính là phản ứng phân hạch dây chuyền.
- Điều kiện để xảy ra phản ứng phân hạch dây chuyền : gọi k là hệ số nhân nơtron ( là số nơtron trung bình còn lại sau mỗi phân hạch ).
+ nếu k < 1 thì phản ứng dây chuyền không xảy ra.
+ nếu k = 1 thì phản ứng dây chuyền xảy ra với mật độ nơtron không đổi : đây là phản ứng dây chuyền điều khiển được dùng trong nhà máy hạt nhân .
+ nếu k > 1 thì xảy ra phản ứng dây chuyền không điều khiển được , dẫn đến một vụ nổ bom nguyên tử.
Để giảm thiểu số nơtron bị mất mát ra bên ngoài để k ≥ 1 thì khối lượng nhiêu liệu hạt nhân phải có một giá trị tối thiểu được gọi là khối lượng tới hạn của hạt nhân đó ( mth ).
c) Ứng dụng :
- Lò phản ứng hạt nhân là thiết bị tạo ra phản ứng phân hạch dây chuyền điều khiển được .
+ nguyên liệu hạt nhân : \[{}^{235}U\] hay \[239Pu\]
+ thanh điều khiển có chứa Bo, Cd để hấp thụ nơtron thừa.
- Nhà máy điện nguyên tử : chứa lò phản ứng hạt nhân và thiết bị tua bin tao ra điện năng nhờ năng lượng toả ra từ phản ứng phân hạch hạt nhân .
2. Phản ứng nhiệt hạch :
a) phản ứng nhiệt hạch :
- là phản ứng tổng hợp hai hạt nhân nhẹ thành một hạt nhân nặng hơn ở nhiệt độ rất cao và toả ra một năng lượng cực lớn.
Các phản ứng hạt nhân phải có nhiệt độ cỡ 109 0K .
b) Thực hiện phản ứng nhiệt hạch :
- các phản ứng nhiệt hạch trong tự nhiên chỉ xảy ở trong lòng Mặt Trời và các ngôi sao vì ở đó mới có đủ các điều kiện để phản ứng xảy ra như : khí hiđro , heli là chủ yếu ( cấu tạo nên các mặt trời) và nhiệt độ đủ lớn , áp suất cao.
- phản ứng nhiệt hạch nhân tạo : ở trên Trái Đất mới chỉ thực hiện được phản ứng nhiệt hạch không kiểm soát được dưới dạng bom khinh khí ( bom H). Vấn đề kiểm soát được phản ứng nhiệt hạch có ý nghĩa to
lớn vì phản ứng nhiệt hạch toả ra một năng lượng rất lớn mà lại sạch với môi trường, nguyên liệu nhẹ như H xem như là vô tận .
Chú ý : Phản ứng phân hạch và phản ứng nhiệt hạch chính là hai dạng đặc biệt của phản ứng hạt nhân . Nhưng có những dạng bài tập riêng nên được tách riêng thành một phần !
II. PHƯƠNG PHÁP GIẢI BÀI TẬP
Loại 1: Tìm năng lượng toả ra của phản ứng phân hạch, nhiệt hạch khi biết khối lượng và tính năng lượng cho nhà máy hạt nhân hoặc năng lượng thay thế :
- cho khối lượng của các hạt nhân trước và sau phản ứng : M0 và M . Tìm năng lượng toả ra khi xảy 1 phản ứng ( phân hạch hoặc nhiệt hạch ):
Năng lượng toả ra : Q = ( M0 – M ).c2 MeV. (3.1)
- Suy ra năng lượng toả ra trong m gam phân hạch (nhiệt hạch ) : E = Q.N = Q.\[\frac{m}{A}.{{N}_{A}}\] MeV (3.2)
Ví dụ 1: Năng lượng tỏa ra trong quá trình phân chia hạt nhân của 1 kg nguyên tử \[{}_{92}^{235}U\]là 5,13.1026 MeV. Cần phải đốt một lượng than đá bao nhiêu để có một nhiệt lượng như thế. Biết năng suất tỏa nhiệt của than là 2,93.107 J/kg.
A.28 kg B. 28.105 kg C. 28.107 kg D. 28.106 kg
Giải
- Rất đơn giản : để có một năng lượng tương đương với năng lượng của 1 kg \[{}_{92}^{235}U\] thì nhiệt lượng toả ra từ việc đốt năng lượng thay thế phải bằng đúng Q toả ra của 235U.
- Ta có : 1kg \[{}_{92}^{235}U\] tạo Q = 5,13.1026 MeV = 8,208.1013 J.
Suy ra lượng than phải đốt là : m \[=\frac{Q}{2,{{93.10}^{7}}}\approx {{28.10}^{5}}\] kg .
\[\Rightarrow \] Chọn đáp án B.
Ví dụ 2: \[{}_{92}^{235}\]U + \[{}_{0}^{1}\]n → \[{}_{42}^{95}\]Mo + \[{}_{57}^{139}\]La +2\[{}_{0}^{1}\]n là một phản ứng phân hạch của Urani 235. Biết khối lượng hạt nhân : mU = 234,99 u ; mMo = 94,88 u ; mLa = 138,87 u ; mn = 1,0087 u.Cho năng suất toả nhiệt của xăng là 46.106 J/kg . Khối lượng xăng cần dùng để có thể toả năng lượng tương đương với 1 gam U phân hạch ?
- 1616 kg B. 1717 kg C.1818 kg D.1919 kg
Giải
- Số hạt nhân nguyên tử 235U trong 1 gam vật chất U là :
N = \[\frac{m}{A}.{{N}_{A}}\] =\[\frac{1}{235}.6,{{02.10}^{23}}=2,{{5617.10}^{21}}\] hạt .
- Năng lượng toả ra khi giải phóng hoàn toàn 1 hạt nhân 235U phân hạch là:
Q = ( M0 – M ).c2 = ( mU + mn – mMo– mLa – 2mn ).c2 = 215,3403 MeV
- Năng lượng khi 1 gam U phản ứng phân hạch :
E = Q.N = 5,5164.1023 MeV = 5,5164.1023 .1,6.10 –3 J = 8,8262 J
- Khối lượng xăng cần dùng để thu được năng lượng của 1 gam 235U phân hạch :
m \[=\frac{Q}{{{46.10}^{6}}}\approx 1919\] kg.
\[\Rightarrow \] Chọn đáp án D
Loại 2: Tìm năng lượng toả ra khi biết độ hụt khối hay năng lượng liên kết
- Xét phản ứng nhiệt hạch : \[{}_{1}^{3}H+{}_{1}^{2}H\to {}_{2}^{4}He+{}_{0}^{1}n\]. Cho biết năng lượng liên kết của \[{}_{1}^{3}H\],\[{}_{1}^{2}H\], \[{}_{2}^{4}H\] . Tìm năng lượng toả ra của phản ứng ?
Ta có : Wlk \[{}_{1}^{2}H\] = mp + mn – \[m({}_{1}^{2}H)\] \[\Rightarrow \] \[m({}_{1}^{2}H)\] = mp + mn – Wlk \[{}_{1}^{2}H\]
Wlk \[{}_{1}^{3}H\] = mp + 2mn – \[m({}_{1}^{3}H)\] \[\Rightarrow \]\[m({}_{1}^{3}H)\]= mp + 2mn – Wlk \[{}_{1}^{3}H\]
Wlk \[{}_{2}^{4}He\] = 2mp + 2mn – \[m({}_{2}^{4}He)\] \[\Rightarrow \]\[m({}_{2}^{4}He)\]= 2mp + 2mn – Wlk \[{}_{2}^{4}He\]
\[\Rightarrow \] năng lượng toả ra : Q = \[m({}_{1}^{2}H)\]+\[m({}_{1}^{3}H)\] – \[m({}_{2}^{4}He)\] – mn
= Wlk \[{}_{2}^{4}He\]– Wlk \[{}_{1}^{2}H\]– Wlk \[{}_{1}^{3}H\] = Wlk \[{}_{2}^{4}He\] – (Wlk \[{}_{1}^{2}H\]+ Wlk \[{}_{1}^{3}H\])
Tổng quát lên : Q = ∑ Wlk sau – ∑ Wlk trước . (3.3)
- Xét phản ứng : \[{}_{1}^{2}H+{}_{1}^{2}H\to {}_{2}^{3}He+{}_{0}^{1}n\] . Cho biết độ hụt khối của \[{}_{1}^{2}H\],\[{}_{2}^{3}He\]. Tìm năng lượng toả ra ?
Ta có : Δm \[{}_{1}^{2}H\]= mp + mn – \[m({}_{1}^{2}H)\] \[\Rightarrow \] \[m({}_{1}^{2}H)\] = mp + mn – Δm \[{}_{1}^{2}H\]
Δm \[{}_{2}^{3}He\]= 2mp + mn – \[m({}_{2}^{3}He)\] \[\Rightarrow \] \[m({}_{2}^{3}He)\]= 2mp + mn – Δm\[{}_{2}^{3}He\]
\[\Rightarrow \] năng lượng toả ra : Q = 2\[m({}_{1}^{2}H)\] - \[m({}_{2}^{3}He)\] - mn = Δm\[{}_{2}^{3}He\]–2Δm \[{}_{1}^{2}H\].
Tổng quát lên : Q = (∑ Δm sau – ∑ Δm trước)c2. (3.4)
Ví dụ 1:[09A] : Cho phản ứng hạt nhân:\[{}_{1}^{2}D+{}_{1}^{3}T\to {}_{2}^{4}He+X\]. Lấy độ hụt khối của hạt nhân T, hạt nhân D, hạt nhân He lần lượt là 0,009106 u; 0,002491 u; 0,030382 u và 1u = 931,5 MeV/c2 . Năng lượng tỏa ra của phản ứng xấp xỉ bằng :
A. 15,017 MeV. B. 17,498 MeV. C. 21,076 MeV. D. 200,025 MeV.
Giải
- Đây là phản ứng nhiệt hạch toả năng lượng được tính theo độ hụt khối của các chất.
Phải xác định đầy đủ độ hụt khối các chất trước và sau phản ứng. Nên ta phải xác định hạt nhân X là :
X ≡ \[{}_{0}^{1}n\] là một nơtron nên có Δm = 0.
- Vậy năng lượng toả ra cảu phản ứng bằng :
Q = ( ∑ Δm sau – ∑ Δm trước)c2 = (ΔmHe + Δmn – ΔmH + ΔmT ).c2 = 17,498 MeV .
\[\Rightarrow \] Chọn đáp án : B
Ví dụ 2: Tìm năng lượng tỏa ra khi một hạt nhân ${}_{92}^{234}\text{U}$ phóng xạ tia α và tạo thành đồng vị Thôri ${}_{90}^{230}\text{Th}$. Cho các năng lượng liên kết riêng của hạt α là 7,1 MeV, của 234U là 7,63 MeV, của 230Th là 7,7 MeV.
- 10,82 MeV. B. 13,98 MeV. C. 11,51 MeV. D. 17,24 MeV.
Giải
- Đây là bài toán tính năng lượng toả ra của một phân rã phóng xạ khi biết Wlk của các hạt nhân trong phản ứng .
- Do đó ta phải xác định được Wlk từ dữ kiện Wlk riêng của đề bài.
Ta có sự phóng xạ diễn ra như sau : ${}_{92}^{234}\text{U}$ → ${}_{90}^{230}\text{Th}$ + α .
Năng lượng liên kết của các hạt nhân là :
Wlk U = 7,63.234 = 1785,42 MeV , Wlk Th = 7,7.230 = 1771 MeV , Wlk α = 7,1.4= 28,4 MeV
- Áp dụng công thức ta có năng lượng toả ra phân rã trên là:
Q = ∑ Wlk sau – ∑ Wlk trước = Wlk Th + Wlk α – Wlk U = 13,98 MeV
\[\Rightarrow \] Chọn đáp án : B
IV.PHẢN ỨNG HẠT NHÂN
I. TÓM TẮT LÍ THUYẾT
1. Phản ứng hạt nhân :
- là mọi quá trình dẫn đến sự biến đổi hạt nhân .
- Phản ứng hạt nhân thương được chia thành hai loại :
Phản ứng tương tác : giữa hai hạt nhân dẫn đến sự biến đổi của chúng thành các hạt nhân khác .
Phản ứng tự phân rã của một hạt nhân không bền (hạt nhân mẹ) thành các hạt nhân khác (hạt nhân con) và kèm theo các tia phóng xạ .
2. Các định luật bảo toàn trong phản ứng hạt nhân :
A + B → C + D.
a) Định luật bảo toàn số nuclôn ( số khối) :
Trong phản ứng hạt nhân, tổng số nuclon của các hạt tương tác bằng tổng số nuclon của các hạt sản phẩm.
Ta có : AA + AB = AC + AD.
b) Định luật bảo toàn điện tích :
Tổng đại số các điện tích của các hạt tương tác bằng tổng đại số các điện tích của các hạt sản phẩm.
Ta có : ZA +ZB = ZC + ZD
c) Định luật bảo toàn năng lượng toàn phần : gồm cả động năng và năng lượng nghỉ.
Tổng năng lượng toàn phần của các hạt tương tác bằng tổng năng lượng toàn phần của các hạt sản phẩm .
Ta có : WA + WB + mA.c2 + mB.c2 = WC + WD + mC.c2 + mD.c2
\[\Leftrightarrow \] WA + WB + Q = WC + WD .
Với Q là năng lượng của phản ứng hạt nhân ( kể cả dấu để xem là thuộc loại phản ứng toả hay thu nhiệt mà sẽ đề cập ở phần dưới ).
d) Định luật bảo toàn động lượng :
Vector tổng động lượng của các hạt tương tác bằng vector tổng động lượng của các hạt sản phẩm.
Ta có : \[\overset{\to }{\mathop{{{p}_{A}}}}\,+\overset{\to }{\mathop{{{p}_{B}}}}\,=\overset{\to }{\mathop{{{p}_{C}}}}\,+\overset{\to }{\mathop{{{p}_{D}}}}\,\].
3. Năng lượng trong phản ứng hạt nhân :
Trong phản ứng hạt nhân có thể là phản ứng toả nhiệt hoặc thu nhiệt. Với M0 = mA + mB là tổng khối lượng nghỉ của các hạt nhân trước phản ứng . M = mC + mD là tổng khối lượng nghỉ của các hạt nhân sau phản ứng . Khi đó năng lượng của một phản ứng hạt nhân có giá trị :
Q = ( M0 – M ).c2 = Δm.c2
+ nếu Q > 0 : phản ứng toả nhiệt .
+nếu Q < 0 : phản ứng thu nhiệt .
II. PHƯƠNG PHÁP GIẢI BÀI TẬP
Loại 1: Xác định hạt nhân còn thiếu và số hạt ( tia phóng xạ ) trong phản ứng hạt nhân .
a) Xác định tên hạt nhân còn thiếu :
- Áp dụng định luật bảo toàn số khối và điện tích .
Chú ý : nên học thuộc một vài chất có số điện tích thường gặp trong phản ứng hạt nhân (không cần quan tâm đến số khối vì nguyên tố loại nào chỉ phụ thuộc vào Z : số thứ tự trong bảng HTTH .
- Một vài loại hạt phóng xạ và đặc trưng về điện tích, số khối của chúng :
hạt α ≡ \[{}_{2}^{4}\]He , hạt nơtron ≡ \[{}_{0}^{1}\]n , hạt proton ≡ \[{}_{1}^{1}\]p , tia β─ ≡ \[{}_{-1}^{0}\]e , tia β+ ≡ \[{}_{+.1}^{0}\]e , tia γ có bản chất là sóng điện từ.
b) Xác định số các hạt ( tia ) phóng xạ phát ra của một phản ứng :
- Thông thường thì loại bài tập này thuộc phản ứng phân hạch hạt nhân . Khi đó hạt nhân mẹ sau nhiều
lần phóng xạ tạo ra x hạt α và y hạt β ( chú ý là các phản ứng chủ yếu tạo loại β– vì nguồn phóng xạ β+ là rất hiếm ) . Do đó khi giải bài tập loại này cứ cho đó là β– , nếu giải hệ hai ẩn không có nghiệm thì mới giải với β+ - nhưng mà chắc không có đâu
Ví dụ 1 : Tìm hạt nhân X trong phản ứng hạt nhân sau :
\[{}_{5}^{10}\]Bo + X → α + \[{}_{4}^{8}\]Be
A. \[{}_{1}^{3}\]T B. \[{}_{1}^{2}\]D
C. \[{}_{0}^{1}\]n D.\[{}_{1}^{1}\]p
Giải:
- Trước tiên phải xác định đầy hạt α có Z và A bằng bao nhiêu . α ≡ \[{}_{2}^{4}\]He nên áp dụng định luật bảo toàn số khối và điện tích. Khi đó suy ra : X có điện tích Z = 2+ 4 – 5 =1
và số khối A = 4 + 8 – 10 = 2.
- Vậy X là hạt nhân \[{}_{1}^{2}\]D đồng vị phóng xạ của H.
\[\Rightarrow \] Chọn đáp án B
Ví dụ 2. Cho phản ứng hạt nhân : T + X → α + n . X là hạt nhân .
- nơtron B. proton C. Triti D. Đơtơri
Giải
- Ta phải biết cấu tạo của các hạt khác trong phản ứng : \[{}_{1}^{3}\]T , α ≡ \[{}_{2}^{4}\]He , \[{}_{0}^{1}\]n .
- Áp dụng định luật bảo toàn điện tích và số khối , ta được :
X có điện tích Z = 2 + 0 – 1 = 1 & số khối A = 4 + 1 – 3 = 2 . Vậy X là \[{}_{1}^{2}\]D
\[\Rightarrow \] Chọn đáp án : D
Loại 2. Xác định năng lượng của phản ứng hạt nhân .
- Xét phản ứng hạt nhân : A + B → C + D .
- Khi đó : + M0 = mA + mB là tổng khối lượng nghỉ của các hạt nhân trước phản ứng .
+ M = mC + mD là tổng khối lượng nghỉ của các hạt nhân sau phản ứng .
- Ta có năng lượng của phản ứng được xác định :
Q = ( M0 – M ).c2 = Δm.c2 .
+ nếu Q > 0 : phản ứng toả nhiệt .
+ nếu Q < 0 : phản ứng thu nhiệt .
- Với bài toán tìm năng lượng khi m (g) chất A tham gia phản ứng hạt nhân. Ta sẽ có tổng năng lượng của phản ứng là : \[E=Q.N=Q.\frac{m.{{N}_{A}}}{A}\] MeV.
Ví dụ 1. Thực hiện phản ứng hạt nhân sau : \[{}_{11}^{23}\]Na + \[{}_{1}^{2}\]D → \[{}_{2}^{4}\]He + \[{}_{10}^{20}\]Ne .
Biết mNa = 22,9327 u ; mHe = 4,0015 u ; mNe = 19,9870 u ; mD = 1,0073 u. Phản ứng trên toả hay thu một năng lượng bằng bao nhiêu J ?
- thu 2,2375 MeV B. toả 2,3275 MeV. C.thu 2,3275 MeV D. toả 2,2375 MeV
Giải
- Ta có năng lượng của phản ứng hạt nhân trên là :
Q = ( M0 – M ).c2 = ( mNa + mHe ─ mNe ─ mD )c2 = + 2,3275 MeV.
Dấu “ + ” chứng tỏ đây là phản ứng toả năng lượng .
\[\Rightarrow \] Chọn đáp án B.
Ví dụ 2: trong phản ứng phân hạch hạt nhânUrani \[{}_{92}^{235}\]U năng lượng trung bình toả ra khi phân chia một hạt nhân là 200 MeV. Tính năng lượng toả ra trong quá trình phân chia hạt nhân của 1 kg Urani trong lò phản ứng.
A. 8,2.1012 J B. 8,2.1013 J C. 7,6.1012 J D. 7,6.1013 J
Giải:
- Số hạt nhân Urani có trong 1kg Urani:
N =\[\frac{m.{{N}_{A}}}{A}\]=\[\frac{{{10}^{3}}6,{{023.10}^{23}}}{235}\]= 2,563.1024 hạt
- Năng lượng toả ra của 1kg Urani:
E0 = N. ΔE = 2,563.1024.200 = 5,126.1026 MeV = 8,2.1013 J
\[\Rightarrow \] Chọn đáp án B
Ví dụ 3: cho phản ứng hạt nhân: \[{}_{1}^{3}\]T + \[{}_{1}^{2}\]D \[\to \] \[{}_{2}^{4}\]He + X +17,6MeV . Tính năng lượng toả ra từ phản ứng trên khi tổng hợp được 2g Hêli.
A. 52,976.1023 MeV B. 5,2976.1023 MeV C. 2,012.1023 MeV D.2,012.1024 MeV
Giải:
- Số nguyên tử hêli có trong 2g hêli:
N =\[\frac{m.{{N}_{A}}}{A}\] = \[\frac{2.6,{{023.10}^{23}}}{4}\]= 3,01.1023 MeV
- Năng lượng toả ra gấp N lần năng lượng của một phản ứng nhiệt hạch:
E = N.Q = 3,01.1023.17,6 = 52,976.1023 MeV
\[\Rightarrow \] Chọn đáp án A.
Loại 3. Động năng và vận tốc của các hạt trong phản ứng hạt nhân .
- Xét phản ứng hạt nhân : A + B → C + D .
- Khi biết khối lượng đầy đủ của các chất tham gia phản ứng .
- Ta sẽ áp dụng định luật bảo toàn năng lượng :
M0c2 + WA +WB = Mc2 + WC +WD
\[\Leftrightarrow \] Q + WA +WB = WC +WD .
Chú ý : dấu của Q là toả năng lượng hay thu năng lượng để khỏi bị nhầm lúc làm toán.
- Khi biết khối lượng không đầy đủ và một vài điều kiện về động năng và vận tốc của hạt nhân .
- Ta sẽ áp dụng định luật bảo toàn động lượng :
\[\overset{\to }{\mathop{{{p}_{A}}}}\,+\overset{\to }{\mathop{{{p}_{B}}}}\,=\overset{\to }{\mathop{{{p}_{C}}}}\,+\overset{\to }{\mathop{{{p}_{D}}}}\,\].
Chú ý : \[{{\left( \overset{\to }{\mathop{p}}\, \right)}^{2}}={{\left( mv \right)}^{2}}=2m.W\]
Ví dụ 1. hạt α bắn vào hạt nhân Al đứng yên gây ra phản ứng : α + \[{}_{13}^{27}\]Al → \[{}_{15}^{30}\]P + n. phản ứng này thu năng lượng Q= 2,7 MeV. Biết hai hạt sinh ra có cùng vận tốc, tính động năng của hạt α . ( coi khối lượng hạt nhân bằng số khối của chúng).
A. 1,3 MeV B. 13 MeV C. 3,1 MeV D. 31 MeV
Giải
- Ta có \[\frac{{{K}_{p}}}{{{K}_{n}}}=\frac{{{m}_{P}}}{{{m}_{n}}}\] =30 \[\Rightarrow \] Kp = 30 Kn
Mà Q = Kα ─ Kp ─ Kn = Kα ─ 31 K n (1)
Áp dụng định luật bảo toàn động lượng: mα .vα = ( mp + mn)v\[\Rightarrow \] 2 mα Kα = 2( mp + mn)( Kp +Kn)
\[\Leftrightarrow \] 4 Kα = 31( Kp + Kn)= 961 Kn \[\Rightarrow \] Kn= \[\frac{4{{K}_{\alpha }}}{961}\]
Thay vào (1) ta có Q =\[\frac{27{{K}_{\alpha }}}{31}\] \[\Rightarrow \] Kα = \[\frac{31Q}{27}=\frac{31}{27}.2,7=3,1MeV\]
\[\Rightarrow \] Chọn đáp án C.
Ví dụ 2: người ta dùng hạt prôtôn có động năng Wp= 2,69 MeV bắn vào hạt nhân Liti đứng yên thu được 2 hạt α có cùng động năng . cho mp = 1,,0073u; mLi = 7,0144u; m α =4,0015u ; 1u = 931 MeV/c2 . tính động năng và vận tốc của mổi hạt α tạo thành?
A. 9,755 MeV ; 3,2.107m/s B.10,55 MeV ; 2,2.107 m/s
C. 10,55 MeV ; 3,2.107 m/s D. 9,755.107 ; 2,2.107 m/s.
Giải
Năng lượng của phản ứng hạt nhân là : Q = ( M0 – M ).c2 = 0,0187uc2 = 17,4097 MeV.
Áp dụng định luật bảo toàn năng lượng ta có Q +Wp= 2W α \[\Rightarrow \] W α =\[\frac{Q+{{W}_{p}}}{2}=10,05MeV\]
Vận tốc của mổi hạt α là: v = \[c\sqrt{\frac{2{{W}_{\alpha }}}{931.4,0015}}\]=2,2.107m/s.
\[\Rightarrow \] Chọn đáp án B.
Ví dụ 3: Một nơtơron có động năng Wn = 1,1 MeV bắn vào hạt nhân Liti đứng yên gây ra phản ứng:
\[{}_{0}^{1}\] n + \[{}_{3}^{6}\]Li → X+ \[{}_{2}^{4}\]He .
Biết hạt nhân He bay ra vuông góc với hạt nhân X. Động năng của hạt nhân X và He lần lượt là :?
Cho mn = 1,00866 u;mx = 3,01600u ; mHe = 4,0016u; mLi = 6,00808u.
A.0,12 MeV & 0,18 MeV B.0,1 MeV & 0,2 MeV
C.0,18 MeV & 0,12 MeV D. 0,2 MeV & 0,1 MeV
Giải
- Ta có năng lượng của phản ứng là : : Q = ( mn+ mLi─ m x ─ m He).c2 = - 0,8 MeV ( đây là phản ứng thu năng lượng )
- Áp dụng định luật bảo toàn động lượng: \[\overset{\to }{\mathop{pn}}\,=\overset{\to }{\mathop{{{p}_{He}}}}\,+\overset{\to }{\mathop{{{p}_{X}}}}\,\]\[\Leftrightarrow \] \[P_{n}^{2}=P_{He}^{2}+P_{X}^{2}\]
\[\Rightarrow \] 2mnWn= 2mHe .W He + 2mx Wx (1)
- Áp dụng định luật bảo toàn năng lượng :Q =Wx +W He ─Wn = -0,8 (2)
.png)
\[\Rightarrow \] Chọn đáp án B
BÀI TẬP VẬN DỤNG
Câu 1. Năng lượng nhỏ nhất để tách hạt nhân He thành hai phần giống nhau là bao nhiêu ? Cho mHe = 4,0015u; mn = 1,0087u; mp = 1,0073u; 1u.c2 = 931MeV
A. 3,2 MeV. B. 12,4 MeV. C. 16,5 MeV. D. 23,8 MeV.
Câu 2. Năng lượng liên kết cho một nuclon trong các hạt nhân 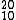 Ne ; He và
Ne ; He và 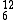 C tương ứng bằng 8,03 MeV ; 7,07 MeV và 7,68 MeV. Năng lượng cần thiết để tách một hạt nhân
C tương ứng bằng 8,03 MeV ; 7,07 MeV và 7,68 MeV. Năng lượng cần thiết để tách một hạt nhân 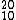 Ne thành hai hạt nhân
Ne thành hai hạt nhân 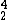 He và một hạt nhân
He và một hạt nhân  C là :
C là :
A. 11,9 MeV. B. 10,8 MeV. C. 15,5 MeV. D. 7,2 MeV.
Câu 3. Tính năng lượng liên kết tạo thành Cl37, cho biết: Khối lượng của nguyên tử \[{}_{17}^{37}\]Cl = 36,96590 u; khối lượng proton, mp = 1,00728 u; khối lượng electron, me = 0,00055 u; khối lượng nơtron, mn = 1,00867 u; 1u = 1,66043.10-27kg; c = 2,9979.108 m/s; 1J = 6,2418.1018 eV.
- A. 316,82 MeV B. 318,14 MeV C. 315,11 MeV D. 317,26 MeV
Câu 4. Hạt nhân Li có khối lượng 7,0144u. Năng lượng liên kết của hạt nhân là bao nhiêu ? Cho mn = 1,0087u ; mp = 1,0073u ; 1u.c2 = 931MeV .
- 45,6 MeV. B. 36,2 MeV. C. 39,4 MeV. D. 30,7 MeV.
Câu 5. Năng lượng cần thiết để bứt một nơtrôn khỏi hạt nhân  Na là bao nhiêu ? Cho mNa = 22,9837u ; mn = 1,0087u ; mp=1,0073u, 1u.c2 = 931MeV
Na là bao nhiêu ? Cho mNa = 22,9837u ; mn = 1,0087u ; mp=1,0073u, 1u.c2 = 931MeV
A. 3,5 MeV. B. .8,1 MeV. C. 12,4 MeV. D. 17,4 MeV
Câu 6: Chọn câu trả lời đúng. Tính số phân tử nitơ trong 1 gam khí niơ. Biết khối lượng nguyên tử lượng của nitơ là 13,999 u. Biết 1u =1,66.10-24 g.
A . 43.1020 hạt . B . 43.1021 hạt C. 215.1021 .hạt D. 215.1020 hạt
Câu 7. Năng lượng liên kết riêng của 235U là 7,7 MeV thì khối lượng hạt nhân U235 là bao nhiêu ? Biết mp=1,0073u; mn=1,0087u.
A . 234,0015 u. B. 236,0912 u. C. 234,9731 u. D. 234,1197 u.
Câu 8. Công thức gần đúng cho bán kính hạt nhân là R=R0A\[^{\frac{1}{3}}\] với R0=1,2 fecmi và A là số khối. Khối lượng riêng của hạt nhân là:
A. 0,26.1018 kg/m3. B. 0,35.1018 kg/m3. C. 0,23.1018 kg/m3. D. 0,25.1018 kg/m3
Câu 9. Một chất phóng xạ có hằng số phân rã λ = 1,44.10-3 (h-1). Trong thời gian bao lâu thì 75% hạt nhân ban đầu sẽ bị phân rã ?
- 36 ngày. B. 40,1 ngày. C. 39,2 ngày. D. 37,4 ngày.
Câu 10. Đồng vị phóng xạ đồng \[{}_{29}^{66}\]Cu có chu kì bán rã T = 4,3 phút. Sau thời gian 12,9 phút thì độ phóng xạ của đồng vị này giảm xuống còn bao nhiêu ?
A. 85% B. 87,5% C. 82,5% D. 80%
Câu 11. \[{}_{79}^{200}\]Au là một chất phóng xạ . Biết độ phóng xạ của 3.10 –9 kg chất đó là 58,9 Ci . Chu kì bán rã của Au 200 là bao nhiêu ?
A. 47,9 phút B.74,9 phút C.94,7 phút D. 97,4 phút .
Câu 12. Khi phân tích một mẫu gỗ, người ta thấy có 87,5% số nguyên tử đồng vị phóng xạ \[{}_{6}^{14}\]C đã bị phân rã thành các nguyên tử \[{}_{7}^{14}\]N . Biết chu kì bán rã của C là 5570 năm. Tuổi của mẫu gỗ này là :
A. 17610 năm B.11400năm C.16710năm D. 14100năm
Câu 13. Ban đầu 5 gam Radon Rn là chất phóng xạ với chu kì bán rã T = 3,8 ngày. Độ phóng xạ của lượng Rn trên sau thời gian 9,5 ngày là:
A. 1,22.105 Ci B.1,36.105 Ci C.1,84.105 Ci D.1,92.105 Ci
Câu 14a. Radon là chất phóng xạ có chu kì bán rã T= 3,6 ngày. Tại thời điểm ban đầu có 1,2 g \[{}_{86}^{222}\]Rn, sau khoảng thời gian t = 1,4T thì số nguyên tử Rn còn lại là bao nhiêu ?
A. 1,874.1018 B.2,165.1019 C.1,234.1021 D.2,465.1020
Câu 14b. Một chất phóng xạ có hằng số phóng xạ bằng 1,44.10 –3.h-1. Sau thời gian bao lâu thì 75% số hạt nhân ban đầu bị phân rã hết ?
A.36 ngày B. 37,4 ngày C.39,2 ngày D.40,1 ngày
Câu 15. \[{}_{92}^{238}\]U sau nhiều lần phóng xạ hạt α và β – biến thành hạt nhân \[{}_{82}^{206}\]Pb. Biết chu kì bán rã của sự biến đổi tổng hợp này là 4,6.109 năm. Giả sử ban đầu một loại đá chỉ chứa \[{}_{92}^{238}\]U không chứa \[{}_{82}^{206}\]Pb. Hiệnnay tỉ lệ khối lượng các chất \[{}_{92}^{238}\]U và \[{}_{82}^{206}\]Pb là 37 thì tuổi của mẫu đá là ?
A. 2.107 năm B.2.108 năm C.2.109 năm D.2.1010 năm
Câu 16. Một nguồn phóng xạ có chu kì bán rã T và tại thời điểm ban đầu có 32N0 hạt nhân . Sau các khoảng thời gian T/2, 2T và 3T thì số hạt nhân còn lại lần lượt là ?
- 24N0, 12N0, 6N0 B. 16\[\sqrt{2}\]N0, 8N0, 4N0
- C.16N0, 8N0, 4N0 D. 16\[\sqrt{2}\]N0, 8\[\sqrt{2}\]N0, 4\[\sqrt{2}\]N0
Câu 17. Có bao nhiêu hạt β – được giải phóng trong một giờ từ 1\[\mu g\] đồng vị \[{}_{11}^{23}\]Na. Biết đồng vị phóng xạ \[{}_{11}^{23}\]Na có chu kì bán rã là 15 h.
A. 2,134.1015 hạt B. 4,134.1015 hạt C. 3,134.1015 hạt D. 1,134.1015 hạt
Câu 18. Chất phóng xạ Po có chu kì bán rã là 138 ngày. Tính số hạt nhân Po để có độ phóng xạ là 1 Ci.
A. 1018 hạt B. 50,2.1015 hạt C. 63,65.1016 hạt D. 30,7.1014 hạt
Câu 19. Một gam chất phóng xạ trong 1s phát ra 4,2.1013 hạt β– . Khối lượng nguyên tử của chất phóng xạ này là 58,933 u; 1u = 1,66.10-27 kg . Chu kì bán rã của chất phóng xạ này là ?
A. 1,78.108 s B. 1,68.108 s C. 1,86.108 s D. 1,87.108 s
Câu 20. Chu kì bán rã \[{}_{84}^{211}\]Po là 138 ngày. Khi phóng ra tia anpha poloni biến thành chì. Sau 276 ngày, khối lượng chì được tạo thành từ 1mmg Po là :
A. 0,6391 g. B. 0,3679 g. C. 0,7360 g. D. 0,7810 g.
Câu 21. Một chất phóng xạ có chu kỳ bán rã T =10s. Lúc đầu có độ phóng xạ 2.107 Bq để cho độ phóng xạ giảm xuống còn 0,25.107 Bq thì phải mất một khoảng thời gian bao lâu:
A . 30 s. B. 20 s. C. 15 s. D. 25 s.
Câu 22. Phốtpho có chu kỳ bán rã là 14 ngày. Ban đầu có 300g chất phốt pho sau 70 ngày đêm, lượng phốt pho còn lại là :
A . 7,968 g. B. 7,933 g. C. 8,654 g. D. 9,735 g
Câu 23 Chọn câu đúng. Vho phản ứng hạt nhân sau: \[{}_{1}^{2}D+{}_{1}^{3}T\to {}_{2}^{4}He{}_{0}^{1}n\] .Biết độ hụt khối tạo thành các hạt nhân.\[{}_{1}^{2}D,{}_{1}^{3}T\] và lần lượt là:ΔmD= 0,0024u; ΔmT= 0,0087u; ΔmHe= 0,0305u;. Cho \[1u=931MeV/{{c}^{2}}\]. Năng lượng tỏa ra của phản ứng là:
A . 180,6 MeV. B18,06 eV. C.18,06 MeV. D . 1,806 MeV.
Câu 24.Dùng hạt prôton có động năng làWp = 5,58MeV bắn vào hạt nhân \[{}_{11}^{23}\]Na đang đứng yên ta thu được hạt α và hạt nhân Ne . cho rằng khồng có bức xạ γ kèm theo trong phản ứng và động năng hạt α là W α = 6,6 MeV của hạt Ne là 2,64MeV .Tính năng lượng toả ra trong phản ứng và góc giữa vectơ vận tốc của hạt α và hạt nhân Ne ?(xem khối lượng của hạt nhân bằng số khối của chúng)
A. 3,36 MeV; 1700 B. 6,36 MeV; 1700 C. 3,36 MeV; 300 D . 6,36 MeV; 300
Câu 25. Dùng hạt prôton có động năng làWp = 3,6MeV bắn vào hạt nhân\[{}_{3}^{7}\]Li đang đứng yên ta thu được2 hạt X giống hệt nhau có cùng động năng .tính động năng của mổi hạt nhân X?
Cho cho mp = 1,,0073u; mLi = 7,0144u; m X = 4,0015u ; 1u = 931 MeV/c2
A.8,5MeV B.9,5MeV C.10,5MeV D.7,5MeV
Câu 26.Đồng vị \[{}_{92}^{234}\]U phóng xạ α biến thành hạt nhân Th không kèm theo bức xạ γ .tính năng lượng của phản ứng và tìm động năng , vận tốc của Th? cho m α = 4,0015u; mU =233,9904u ; mTh=229,9737u; 1u = 931MeV/c2
A. thu 14,15MeV; 0,242MeV; 4,5.105 m/s B. toả 14,15MeV; 0,242 MeV; 4,5.105 m/s
C. toả 14,15MeV; 0,422MeV; 5,4.105 m/s D. thu 14,15MeV; 0,422MeV; 5,4.105 m/s
Câu 27Hạt α có động năng W α = 4MeV bắn vào hạt nhân Nitơ đang đứng yên gây ra phản ứng :
α + \[{}_{7}^{14}\]N ─> \[{}_{1}^{1}\]H + X
Tìm năng lượng của phản ứng hạt nhân và vận tốc của hạt nhân X . Biết hai hạt sinh ra có cùng động năng . Cho m α = 4,002603u ; mN = 14,003074u; mH = 1,0078252u; mX = 16,999133u;1u = 931,5 MeV/c2
A. toả 11,93MeV; 0,399.107 m/s B. thu 11,93MeV; 0,399.107 m/s
C. toả 1,193MeV; 0,339.107 m/s D. thu 1,193MeV; 0,399.107 m/s.
Câu 28. \[{}_{88}^{226}\]Ra là hạt nhân phóng xạ sau một thời gian phân rã thành một hạt nhân con và tia α .
Biết mRa = 225,977 u; mcon = 221,970 u ; m α = 4,0015 u; 1u = 931,5 MeV/c2
Tính động năng hạt α và hạt nhân con khi phóng xạ Radi
A. 5,00372MeV; 0,90062MeV B. 0,90062MeV; 5,00372MeV
C. 5,02938MeV; 0,09062MeV D. 0,09062MeV; 5,02938MeV.
Câu 29.Chọn câu trả lời đúng. Prôtôn bắn vào nhân bia đứng yên Liti ( \[{}_{3}^{7}Li\]). Phản ứng tạo ra hai hạt X giống hệt nhau bay ra. Hạt X là :
A. Đơtêri B. Prôtôn C. Nơtron. D. Hạt α
Câu 30.Chọn câu trả lời đúng. Hạt nhân \[{}_{92}^{238}U\] sau khi phát ra các bức xạ α và β cuối cùng cho đồng vị bền của chì \[{}_{82}^{206}Pb\]. Số hạt α và β phát ra là:
A . 8 hạt α và 10 hạt β+ B. 8 hạt α và 6 hạt β-. C .4 hạt α và 2 hạt β+. D. 8 hạt α và 8 hạt β-
Câu 31.Chọn câu đúng. Xét phóng xạ :\[{}_{Z}^{A}Y\to \alpha +{}_{{{Z}_{X}}}^{{{A}_{X}}}.X\]. Trong đó Zx và Ax.
A Zx = Z – 2 và Ax= A – 2. B . Zx = Z và Ax = A. C . Zx = Z – 2 và Ax= A– 4. D Zx = Z +1 và Ax= A.
Câu 32.Khi một hạt nhân nguyên tử phóng xạ lần lượt một tia a rồi một tia b- thì hạt nhân nguyên tử sẽ biến đổi như thế nào?
A. Số khối giảm 4, số prôtôn giảm 1. B. Số khối giảm 4, số prôtôn tăng 1.
C. Số khối giảm 4, số prôtôn giảm 2. D. Số khối giảm 2, số prôtôn giảm 1.
ĐÁP ÁN
1D 2A 3D 4C 5D 6B 7D 8C 9C 10B
11A 12C 13B 14aC 14bD 15B 16B 17D 18C 19B 20 C
21A 22D 23C 24A 25C 26B 27D 28C 29D 30B
31C 32A







