Câu 1: Một con lắc lò xo khối lượng vật nặng 100 g, độ cứng lò xo 10 N/m, treo thẳng đứng. Từ vị trí cân bằng kéo con lắc để lò xo giãn 20 cm rồi thả nhẹ. Chọn gốc thời gian lúc thả vật. Tìm thời điểm lần thứ hai lò xo giãn 5 cm.
A. 4,2 s B. 0,42 s C. 0,21 s D. 2,1 s
Hướng dẫn
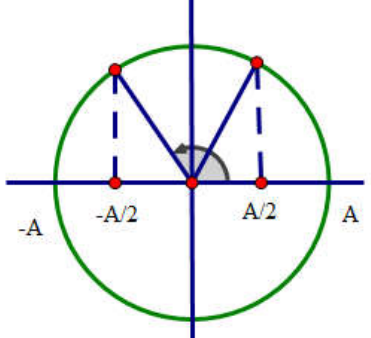
Chu kì dao động là \[T=2\pi \sqrt{\frac{m}{k}}=0,63s\]
Nhìn trên hình vẽ ta có \[\Delta \varphi =\frac{2\pi }{3}\to \Delta t=\frac{T}{3}=0,21s\]
Chọn đáp án C
Câu 2: Một vật dao động điều hòa trên trục Ox. Khoảng thời gian ngắn nhất từ khi gia tốc của vật đạt giá trị cực tiểu tới khi vận tốc của vật đạt giá trị cực đại là 0,5 s. Thời điểm ban đầu, lực kéo về có giá trị cực đại. Thời điểm vật có li độ x và vận tốc v thỏa mãn \[v=\omega x\] lần thứ 2016 là
A. 671,583 s. B. 503,875 s. C. 671,917 s. D. 503,725 s.
Hướng dẫn
Khoảng thời gian ngắn nhất từ khi gia tốc của vật đạt giá trị cực tiểu tới khi vận tốc của vật đạt giá trị cực đại là 0,5 s suy ra ta có \[\Delta t=\frac{T}{2}+\frac{T}{4}=0,5s\to T=\frac{2}{3}s\]
Thời điểm ban đầu, lực kéo có giá trị cực đại suy ra \[{{x}_{o}}=-A\]
Trong 1 chu kì có 2 vị trí thỏa mãn \[v=\omega x\]là \[x=\frac{A}{\sqrt{2}}\]theo chiều dương và \[x=-\frac{A}{\sqrt{2}}\] theo chiều âm.
suy ra \[{{t}_{2}}=\frac{7T}{8}\to {{t}_{2016}}={{t}_{2}}+\frac{2016-2}{2}T=671,917\]
Chọn đáp án C
Câu 3: Sóng cơ hình sin truyền từ M đến N, bước sóng 30 cm, chu kì 0,5s, biên độ 4 cm. Biết N cách M một khoảng bằng 10 cm. Ở thời ban đầu (t = 0), điểm M có li độ 2 cm và đang đi theo chiều dương. Thời điểm điểm N tới vị trí cân bằng lần thứ 2017 là
A.\[\frac{4033}{8}(s)\] B.\[\frac{4033}{2}(s)\] C.\[\frac{2996}{3}(s)\] D.\[\frac{2996}{6}(s)\]
Hướng dẫn
Ta có \[{{\varphi }_{MN}}=\frac{2\pi }{3}\]
Sử dụng vòng tròn lượng giác ta có: thời điểm từ t=0 tới vị trí N cân bằng lần đầu tiên là T/4.
Vậy khoảng thời gian để qua vị trí cân bằng lần thứ 2017 là: \[\Delta t={{t}_{1}}+\frac{2017-1}{2}T=\frac{T}{4}+1008T=\]\[\frac{4033}{8}(s)\]
Chọn đáp án A
Câu 4: Một sóng cơ học được truyền theo phương Ox với vận tốc v = 20 cm/s. Giả sử khi sóng truyền đi biên độ không thay đổi. Tại O dao động có phương trình \[{{u}_{O}}=4\sin \left( 4\pi \right)mm\] . Trong đó t đo bằng giây. Tại thời điểm \[{{t}_{1}}\] li độ tại điểm O là \[u=\sqrt{3}mm\] và đang giảm. Ở thời điểm \[{{t}_{2}}={{t}_{1}}+\frac{T}{2}\] điểm M cách O một đoạn d = 40 cm sẽ có li độ là
A.\[\sqrt{3}mm\] B.\[-\sqrt{3}mm\] C. 4mm. D. -4mm.
Hướng dẫn
Ta có: \[\lambda =vT=20.0,5=10cm\to OM=4\lambda \] nên M dao động cùng pha với O. Tại \[{{t}_{1}}\] li độ của M \[u=\sqrt{3}mm\] và đang giảm. Vậy tới \[{{t}_{2}}={{t}_{1}}+\frac{T}{2}\] thì điểm M sẽ có li độ là \[-\sqrt{3}mm\]
Chọn đáp án B
Câu 5: Trong một mạch dao động LC không có điện trở thuần, điện tích trên tụ biến thiên theo phương trình \[q=4\cos \left( 1000\pi t-\frac{\pi }{2} \right)\mu C\]. Kể từ thời điểm ban đầu, điện tích trên tụ có giá trị bằng 2\[\mu \]C lần thứ 2017 tại thời điểm
A.\[\frac{24175}{24}(s)\] B.\[\frac{967}{480}(s)\] C.\[\frac{12109}{6000}(s)\] D.\[\frac{12097}{6000}(s)\]
Hướng dẫn
Chu kì \[T=\frac{2}{1000}s\]
Vẽ trục thời gian ta xác định được khoảng thời gian từ t=0 tới \[{{t}_{1}}\] là \[{{t}_{1}}=\frac{T}{12}\]
\[t={{t}_{1}}+\frac{2017-1}{2}T=\]\[\frac{12097}{6000}(s)\]
Chọn đáp án D
Câu 6: Trong một mạch dao động LC không có điện trở thuần, dòng điện qua tụ biến thiên theo phương trình \[i=4\sqrt{2}\cos \left( 1000t-\frac{\pi }{2} \right)\](mA). Kể từ thời điểm ban đầu, điện tích trên tụ có độ lớn bằng \[4\mu C\] lần thứ 2016 tại thời điểm
A.\[\frac{4031\pi }{4000}(s)\] B.\[\frac{126\pi }{125}(s)\] C.\[\frac{504\pi }{125}(s)\] D.\[\frac{252\pi }{125}(s)\]
Hướng dẫn
Chu kì \[T=\frac{2\pi }{1000}s\]
Sử dụng vòng tròn lượng giác tính được khi t =0 thì \[q=-{{Q}_{o}}\]
Khoảng thời gian từ \[-{{Q}_{o}}\] tới vị trí có độ lớn 4 \[\mu \]C lần đầu tiên là \[q=-4\mu C=\frac{-{{Q}_{o}}}{\sqrt{2}}\to t=\frac{T}{8}\]
Trong 1 chu kì có 4 lần điện tích có độ lớn 4 \[\mu \]C nên ta có \[\Delta t=t+\frac{2016-1}{4}T=\frac{T}{8}+\frac{2015}{4}T=\frac{4031T}{8}\]=\[\frac{4031\pi }{4000}(s)\]
Chọn đáp án A
Câu 7: Một vật dao động điều hòa với phương trình \[x=Acos\left( 5\pi t+\frac{\pi }{4} \right)cm\]. Véc tơ vận tốc hướng theo chiều âm, véc tơ gia tốc hướng theo chiều dương của trục Ox trong khoảng thời gian nào sau đây? (kể từ t = 0)
A. 0, 2 s < t < 0,3 s
B. 0, 05 s < t < 0,15 s
C. 0, 3 s < t < 0,4 s
D. 0, 1 s < t < 0,2 s
Hướng dẫn
Vẽ trục thời gian ta dễ thấy véc tơ vận tốc hướng theo chiều âm, véc tơ gia tốc hướng theo chiều dương của trục Ox khi vật đi từ vị trí cân bằng theo chiều âm đến biên âm.
\[\Rightarrow \frac{\pi }{2}+k2\pi \le 5\pi t+\frac{\pi }{4}\le \pi +k2\pi \Leftrightarrow 0,05+0,4k\le t\le 0,15+0,4k\]
Ta thấy đáp án B thỏa mãn.
Chọn đáp án B
Câu 8: Một vật dao động điều hòa với chu kỳ T và biên độ 5 cm. Trong một chu kỳ, khoảng thời gian để tốc độ của vật không vượt quá 20πcm/s là 2T/3. Chu kỳ dao động của vật bằng
A. 0,433 s B. 0,15 s C. 0,25 s D. 0,5 s
Hướng dẫn
Ta có \[{{v}_{\max }}=A\omega \].Dựng đường tròn ứng với vận tốc

Cung tròn ứng với tốc độ của vật không vượt quá 20\[\pi \]cm/s là QaM và NbP
Suy ra thời gian để tốc độ không vượt quá 20\[\pi \]cm/s là \[t=\frac{2\varphi }{\omega }=\frac{2T}{3}\to \varphi =\frac{2\pi }{3}\to MOH=\frac{\varphi }{2}=\frac{\pi }{3}\]
Ta có:\[\cos MOH=\frac{1}{2}=\frac{20\pi }{A\omega }\to \omega =8\pi \to T=0,25s\]
Chọn đáp án C
Câu 9: Một vật dao động điều hòa với phương trình \[x=4\cos \left( \omega t-\frac{\pi }{3} \right)cm\].Trong một chu kỳ dao động, khoảng thời gian mà vật có độ lớn gia tốc \[a>\frac{{{a}_{\max }}}{2}\] là 0,4 s. Tìm khoảng thời gian ngắn kể từ khi vật dao động đến khi vật qua vị trí có tốc độ \[v=\frac{{{v}_{\max }}}{2}\] lần thứ ba?
A. 0,3 s B. 0,4 s C. 0,5 s D. 0,35 s
Hướng dẫn
Trong một chu kỳ dao động, khoảng thời gian mà vật có độ lớn gia tốc \[a>\frac{{{a}_{\max }}}{2}\] là 0,4 s
\[\Rightarrow t=\frac{4T}{6}=\frac{2T}{3}=0,4\Leftrightarrow T=\frac{3}{5}s\]
Khoảng thời gian ngắn kể từ khi vật dao động đến khi vật qua vị trí có tốc độ \[v=\frac{{{v}_{\max }}}{2}\] lần thứ ba là :
\[t=\frac{T}{12}+\frac{T}{6}+\frac{T}{3}=\frac{7T}{12}=0,35s\]
Chọn đáp án D
Câu 10: Một vật dao động điều hòa với phương trình \[x=5\cos \left( \omega t+\frac{\pi }{3} \right)cm\] . Trong một chu kỳ dao động, khoảng thời gian mà tốc độ của vật \[v>\frac{\sqrt{3}{{v}_{\max }}}{2}\]là 0,6 s. Tìm khoảng thời gian ngắn kể từ khi vật dao động đến khi vật qua vị trí có độ lớn gia tốc cực đại?
A. 0,3 s B. 1/15 s C. 1/30 s D. 0,6 s
Hướng dẫn
Trong một chu kỳ dao động, khoảng thời gian mà vật có độ lớn vận tốc \[v>\frac{\sqrt{3}{{v}_{\max }}}{2}\]
là 0,6 s
\[\Rightarrow t=\frac{T}{6}+\frac{T}{6}=\frac{T}{3}=0,6\Leftrightarrow T=1,8s\]
Khoảng thời gian ngắn kể từ khi vật dao động đến khi vật qua vị trí có độ lớn gia tốc \[a={{a}_{\max }}\] là: \[t=\frac{T}{3}=0,6s\]
Chọn đáp án D
Câu 11: Một chất điểm dao động điều hòa với phương trình \[x=4\cos \left( 2\pi t+\frac{\pi }{3} \right)cm\]. Từ thời điểm 1/12 s đến thời điểm 6,25 s khoảng thời gian vật dao động có li độ thỏa mãn \[\left| x \right|\ge 2cm\]xấp xỉ
A. 4,08 s. B. 3 s. C. 5 s. D. 3,58 s.
Hướng dẫn
Thời điểm t=1/12s thì x= 0, v<0.
Thời điểm t=6,25s thì \[x=\frac{-4\sqrt{3}}{2},v<0\]
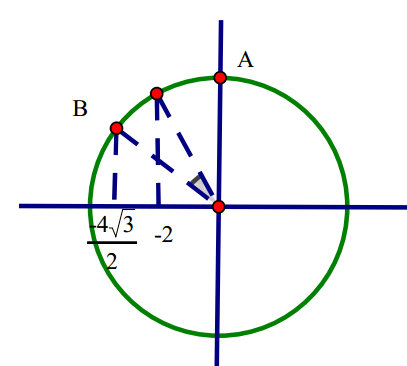
Sử dụng vòng tròn lượng giác ta thấy thời gian để \[\left| x \right|\ge 2cm\] từ A tới B là \[\Delta t=\frac{T}{12}\]
Trong 1 chu kì thời gian để \[\left| x \right|\ge 2cm\] là \[\frac{2T}{3}\]
Vậy từ t=1/12 đến t=6,25s thời gian để \[\left| x \right|\ge 2cm\] là \[\Delta t=2.6.\frac{T}{3}+\frac{T}{12}=\]4,08 s
Chọn đáp án A
Câu 12: Một chất điểm dao động điều hòa với phương trình \[x=4\cos \left( 2\pi t-\frac{\pi }{6} \right)cm\]. Từ thời điểm 1/3 s đến thời điểm 5,5 s khoảng thời gian vật dao động có tốc độ thỏa mãn \[v\le 4\pi \sqrt{3}cm/s\]xấp xỉ
A. 4,18 s. B. 3,42 s. C. 5,15 s. D. 3,85 s
Hướng dẫn
Thời điểm t=1/3s thì \[v=-8\pi \]
Thời điểm t=5,5s thì \[v=\frac{-8\pi }{2}\]
Sử dụng vòng tròn lượng giác ta thấy từ \[{{v}_{1}}=-8\pi \] \[\to {{v}_{2}}=\frac{-{{v}_{\max }}}{2}\] có khoảng thời gian để \[v\le 4\pi \sqrt{3}cm/s\] là \[t=\frac{T}{12}\]
Vậy từ t=1/3s đến t=5,5s thời gian để \[v\le 4\pi \sqrt{3}cm/s\]là \[\Delta t=2.5.\frac{T}{3}+\frac{T}{12}=3,42s\]
Chọn đáp án B
Câu 13: Một sợi dây đàn hồi căng ngang, đầu A cố định. Trên dây đang có sóng dừng ổn định. Gọi B là điểm bụng thứ hai tính từ A, C là điểm nằm giữa A và B. Biết AB = 30 cm, \[AC=\frac{20}{3}cm\], tốc độ truyền sóng trên dây là v = 50 cm/s. Khoảng thời gian ngắn nhất giữa hai lần mà li độ của phần tử tại B bằng biên độ dao động của phần tử tại C là:
A.\[\frac{4}{15}s\] B.\[\frac{1}{15}s\] C.\[\frac{2}{15}s\] D.\[\frac{2}{5}s\]
Hướng dẫn
Ta có: \[AB=\frac{3\lambda }{4}\to \lambda =40cm\to T=0,8s\]
Gọi phương trình sóng tại nguồn là \[u=a\cos \omega t\]
Phương trình sóng tại C là
\[u=2a\cos \frac{2\pi d}{\lambda }\cos \left( \omega t+\frac{\pi }{2} \right)=\sqrt{3}\cos \left( \omega t+\frac{3\pi }{2} \right)\]
Khoảng thời gian ngắn nhất giữa 2 lần liên tiếp mà li độ của phần tử tại B bằng biên độ dao động của phần tử tại C là \[t=\frac{T}{6}=\frac{2}{15}s\]
Chọn đáp án C
Câu 14: Một sợi dây đàn hồi căng ngang, đầu A cố định. Trên dây đang có sóng dừng ổn định với bước sóng 30 cm. Gọi B là điểm bụng gần A nhất, C là điểm nằm giữa A và B. Biết AC = 2BC. Khoảng thời gian ngắn nhất giữa hai lần liên tiếp mà li độ dao động của phần tử tại B bằng biên độ dao động của phần tử tại C là 0,05 s. Tính tốc độ truyền sóng?
A. 100 cm/s B. 60 cm/s C. 120 cm/s D. 80 cm/s
Hướng dẫn
Ta có: \[AB=\frac{\lambda }{4}\to AC=\frac{\lambda }{6}=\]
Biên độ tại C: \[{{A}_{C}}={{A}_{\max }}\left| \sin \frac{2\pi AC}{\lambda } \right|=\frac{{{A}_{\max }}\sqrt{3}}{2}\]
Khoảng thời gian ngắn nhất giữa hai lần liên tiếp li độ của phần tử tại B bằng \[\frac{{{A}_{\max }}\sqrt{3}}{2}\] là \[\frac{T}{6}=0,05s\Rightarrow T=0,3s\]
\[\Rightarrow v=\frac{\lambda }{T}=100cm/s\]
Chọn đáp án A







