
Ví dụ minh họa:

Hướng dẫn:
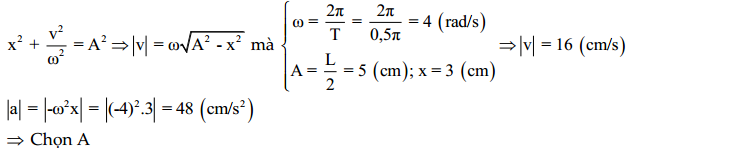

Hướng dẫn:
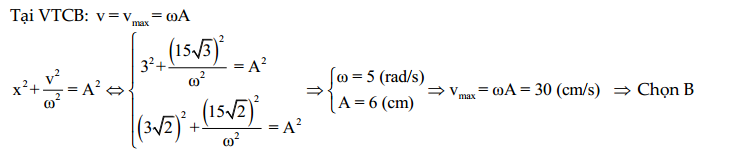

Hướng dẫn:
\[\frac{{{v}^{2}}}{{{\text{ }\!\!\omega\!\!\text{ }}^{2}}}+\frac{{{a}^{2}}}{{{\text{ }\!\!\omega\!\!\text{ }}^{4}}}={{A}^{2}}\xrightarrow{\text{ }\!\!\omega\!\!\text{ }=\sqrt{\frac{k}{m}}=\sqrt{\frac{20}{0,2}}=10}A=\sqrt{\frac{0,{{2}^{2}}}{1{{0}^{2}}}+\frac{{{\left( 2\sqrt{3} \right)}^{2}}}{1{{0}^{4}}}}=0,04 (m)=4 \left( cm \right)\] $\Rightarrow $ Chọn B

Hướng dẫn:
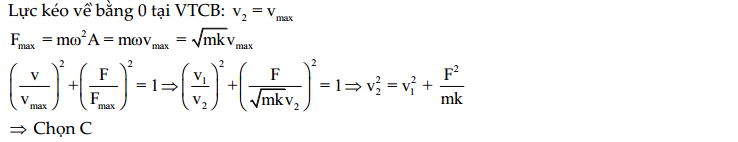
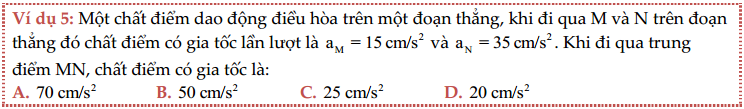
Hướng dẫn:
$\text{x = }\frac{{{\text{x}}_{\text{M}}}\text{ + }{{\text{x}}_{\text{N}}}}{\text{2}}\xrightarrow{\text{a = -}{{\text{ }\!\!\omega\!\!\text{ }}^{\text{2}}}\text{x}}\text{ a = }\frac{{{\text{a}}_{\text{M}}}\text{ + }{{\text{a}}_{\text{N}}}}{\text{2}}\text{ = }\frac{\text{15 + 35}}{\text{2}}\text{ = 25 (cm/}{{\text{s}}^{\text{2}}}\text{)}$ $\Rightarrow $ Chọn C

Hướng dẫn:
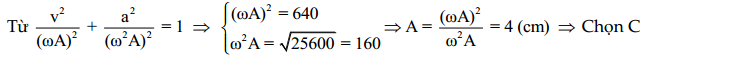

Hướng dẫn:
\[{{\text{x}}^{\text{2}}}\text{ + }\frac{{{\text{v}}^{\text{2}}}}{{{\text{ }\!\!\omega\!\!\text{ }}^{\text{2}}}}\text{ = }{{\text{A}}^{\text{2}}}\Rightarrow \left| \text{x} \right|\text{ = }\sqrt{{{\text{A}}^{\text{2}}}\text{ - }\frac{{{\text{v}}^{\text{2}}}}{{{\text{(2 }\!\!\pi\!\!\text{ f)}}^{\text{2}}}}}\text{ }\Rightarrow \frac{\left| {{\text{x}}_{\text{2}}} \right|}{\left| {{\text{x}}_{\text{1}}} \right|}\text{ = }\frac{\sqrt{{{\text{A}}^{\text{2}}}\text{ - }\frac{{{\text{(4,8 }\!\!\pi\!\!\text{ fA)}}^{\text{2}}}}{\text{(2 }\!\!\pi\!\!\text{ }\text{.4f)}}}}{\sqrt{{{\text{A}}^{\text{2}}}\text{ - }\frac{{{\text{(4,8 }\!\!\pi\!\!\text{ fA)}}^{\text{2}}}}{\text{(2 }\!\!\pi\!\!\text{ }\text{.3f)}}}}\text{ = }\frac{\sqrt{{{\text{A}}^{\text{2}}}\text{ - (0,6A}{{\text{)}}^{\text{2}}}}}{\sqrt{{{\text{A}}^{\text{2}}}\text{ - (0,8A}{{\text{)}}^{\text{2}}}}}\text{ = }\frac{\text{4}}{\text{3}}\text{ = }\frac{\text{12}}{\text{9}}\]
$\Rightarrow $ Chọn B

Hướng dẫn:
\[{{m}_{1}}\omega _{1}^{2}{{A}_{1}}={{m}_{2}}\omega _{2}^{2}{{A}_{2}}\to \frac{{{m}_{2}}}{{{m}_{1}}}=\frac{\omega _{1}^{2}{{A}_{1}}}{\omega _{2}^{2}{{A}_{2}}}={{\left( \frac{{{\omega }_{1}}{{A}_{1}}}{{{\omega }_{2}}{{A}_{2}}} \right)}^{2}}.\frac{{{A}_{2}}}{{{A}_{1}}}\xrightarrow[{{\omega }_{1}}{{A}_{1}}=3{{\omega }_{2}}{{A}_{2}}]{3{{A}_{1}}={{A}_{2}}}\frac{{{m}_{2}}}{{{m}_{1}}}={{3}^{2}}.3=27\] $\Rightarrow $ Chọn D.

Hướng dẫn:
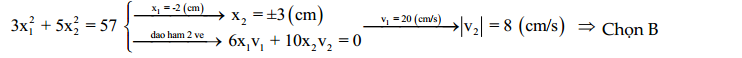
Bài tập tự luyện:
Câu 1: Một vật dao động điều hòa với biên độ A, tần số góc $\text{ }\!\!\omega\!\!\text{ }$. Khi vật cách vị trí cân bằng $\text{0,5A}$ thì tốc độ của vật là:
A. $\text{ }\!\!\omega\!\!\text{ A}$ B. $\frac{\text{ }\!\!\omega\!\!\text{ A}}{\text{2}}$ C. $\frac{\text{ }\!\!\omega\!\!\text{ A}\sqrt{\text{2}}}{\text{2}}$ D. $\frac{\text{ }\!\!\omega\!\!\text{ A}\sqrt{\text{3}}}{\text{2}}$
Câu 2: Một vật dao động điều hòa với biên độ A, vận tốc cực đại là ${{\text{v}}_{\text{max}}}$. Vật có tốc độ $\text{0,6}{{\text{v}}_{\text{max}}}$ khi li độ của vật có độ lớn là:
A. $\text{0,4A}$ B. $\text{0,8A}$ C. $\text{0,6A}$ D. $\text{0,5A}$
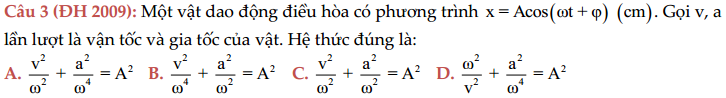
Câu 4: Một vật dao động điều hòa với biên độ A, tần số góc $\omega $. Tại một thời điểm, li độ x, vận tốc v và gia tốc a của vật có hệ thức đúng là:
A. \[\frac{{{\text{v}}^{\text{2}}}}{{{\text{ }\!\!\omega\!\!\text{ }}^{\text{2}}}}\text{ + }\frac{{{\text{a}}^{\text{2}}}}{{{\text{ }\!\!\omega\!\!\text{ }}^{\text{2}}}}\text{ = }{{\text{A}}^{\text{2}}}\] B. \[\frac{{{\text{x}}^{\text{2}}}}{{{\text{ }\!\!\omega\!\!\text{ }}^{\text{2}}}}\text{ + }\frac{{{\text{a}}^{\text{2}}}}{{{\text{ }\!\!\omega\!\!\text{ }}^{\text{4}}}}\text{ = }{{\text{A}}^{\text{2}}}\] C. $\text{a = - }\!\!\omega\!\!\text{ x}$ D. $\text{a = -}{{\text{ }\!\!\omega\!\!\text{ }}^{\text{2}}}\text{x}$
Câu 5 (CĐ-2012): Một vật dao động điều hòa với tần số góc $5\text{ rad/s}$. Khi vật đi qua li độ $5\text{ cm}$ thì nó có tốc độ là $25\text{ cm/s}$. Biên độ dao động của vật là:
A. $5,24\text{ cm}$ B. $5\sqrt{2}\ cm$ C. $5\sqrt{3}\text{ cm}$ D. $10\text{ cm}$
Câu 6 (CĐ-2011): Một vật dao động điều hòa với chu kì 2 s, biên độ 10 cm. Khi vật cách vị trí cân bằng 6 cm thì tốc độ của nó bằng:
A. $12,56\text{ cm/s}$ B. $20,08\text{ cm/s}$ C. $25,13\text{ cm/s}$ D. $18,84\text{ cm/s}$
Câu 7: Một vật dao động điều hòa với biên độ 5 cm. Khi vật có li độ là 4 cm thì vận tốc là $\text{6 }\!\!\pi\!\!\text{ }$ cm/s. Tần số dao động của vật là:
A. $\operatorname{f}=1 Hz$ B. $\operatorname{f}=1,2 Hz$ C. $\operatorname{f}=3 Hz$ D. $\operatorname{f}=4,6 Hz$
Câu 8 (ĐH-2011): Một chất điểm dao động điều hòa trên trục Ox. Khi chất điểm đi qua vị trí cân bằng thì tốc độ của nó là $20\text{ cm/s}$. Khi chất điểm có tốc độ là $10\text{ cm/s}$ thì gia tốc của nó có độ lớn là $40\sqrt{3}\text{ cm/}{{\text{s}}^{2}}$. Biên độ dao động của chất điểm là:
A. $5\text{ cm}$ B. $4\text{ cm}$ C. $10\text{ cm}$ D. $8\text{ cm}$
Câu 9: Một chất điểm dao động điều hòa trên trục Ox với chu kì 2 s và biên độ 9 cm. Tại thời điểm t, lực hồi phục tác dụng lên vật có độ lớn $\operatorname{F}=0,15\ N$ và động lượng của vật lúc đó là $\text{p = 37,5}\sqrt{\text{2}}\text{ gm/s}$. Lấy \[{{\text{ }\!\!\pi\!\!\text{ }}^{\text{2}}}\text{ = 10}\]. Khối lượng của vật nặng là:
A. 0,15 kg B. 0,25 kg C. 0,12 kg D. 0,2 kg

Câu 11: Một con lắc lò xo nằm ngang gồm quả nặng có khối lượng $\operatorname{m}=100\ g$ thực hiện dao động điều hòa. Khi chất điểm ở cách vị trí cân bằng 6 cm thì tốc độ của vật bằng $\text{0,4}\ \text{m/s}$ và lực kéo về tác dụng lên vật có độ lớn bằng 0,15 N. Biên độ dao động chất điểm là:
A. 4cm B. $5\sqrt{5}$ cm C. 5 cm D. 10 cm
Câu 12: Một vật dao động điều hòa có vận tốc và tọa độ tại thời điểm ${{t}_{1}}$ và ${{t}_{2}}$ tương ứng là: ${{\operatorname{v}}_{1}}=20 cm/s$, ${{\operatorname{x}}_{1}}=8\sqrt{3} cm$ và ${{\operatorname{v}}_{2}}=20\sqrt{2} cm/s$, ${{\operatorname{x}}_{2}}=8\sqrt{2} cm$. Vận tốc cực đại của vật dao động là:
A. $40\sqrt{2}\text{ cm/s}$ B. $40\text{ cm/s}$ C. $40\sqrt{3}\text{ cm/s}$ D. $\text{80 cm/s}$
Câu 13: Một chất điểm dao động điều hòa trên trục Ox. Tại thời điểm ${{\operatorname{t}}_{1}}, {{t}_{2}}$ vận tốc và gia tốc của vật có giá trị tương ứng là ${{v}_{1}}=10\sqrt{3}\text{ cm/s, }{{\text{a}}_{1}}=-1\text{ m/}{{\text{s}}^{2}}$ và ${{\text{v}}_{\text{2}}}\text{ = -10 cm/s}$, ${{\text{a}}_{\text{2}}}\text{ = -}\sqrt{\text{3}}\text{ m/}{{\text{s}}^{\text{2}}}$. Li độ tại thời điểm ${{\text{t}}_{\text{2}}}$ của vật là:
A. $-1\text{ cm}$ B. $\text{1 cm}$ C. $\frac{1}{\sqrt{3}}\text{ cm}$ D. $\text{3}\ \text{cm}$
Câu 14: Động lượng và gia tốc của một vật nặng 1 kg dao động điều hòa tại các thời điểm ${{\text{t}}_{\text{1}}}\text{, }{{\text{t}}_{\text{2}}}$ có giá trị tương ứng \[{{\operatorname{p}}_{1}} = 0,12\ kgm/s\], ${{\operatorname{p}}_{2}} = 0,16\ kgm/s$, ${{\operatorname{a}}_{1}} = 0,64\ m/{{s}^{2}}$, ${{\operatorname{a}}_{2}} = 0,48\ m/{{s}^{2}}$. Động năng biến thiên với chu kì:
A. $\text{0,25 }\!\!\pi\!\!\text{ }\ \text{s}$ B. $\text{0,125 }\!\!\pi\!\!\text{ }\ \text{s}$ C. $\text{0,5 }\!\!\pi\!\!\text{ }\ \text{s}$ D. $\text{0,5}\ \text{s}$
Câu 15: Trong dao động điều hòa, gọi tốc độ và gia tốc tại hai thời điểm khác nhau lần lượt là ${{\text{v}}_{\text{1}}}\text{, }{{\text{v}}_{\text{2}}}$ và ${{\text{a}}_{\text{1}}}\text{, }{{\text{a}}_{\text{2}}}$thì tần số góc được xác định bởi biểu thức nào sau đây là đúng?
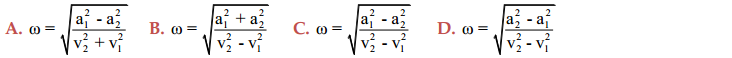
Câu 16: Một vật dao động điều hòa với biên độ A quanh vị trí cân bằng O. Ở vị trí M, vật có li độ ${{\text{x}}_{\text{1}}}$ và tốc độ ${{\text{v}}_{\text{1}}}$. Ở vị trí N, vật có li độ ${{\text{x}}_{\text{2}}}$ và tốc độ ${{\text{v}}_{\text{2}}}$. Biên độ A là:
A. $\sqrt{\frac{\text{v}_{\text{1}}^{\text{2}}\text{x}_{\text{2}}^{\text{2}}\text{ + v}_{\text{2}}^{\text{2}}\text{x}_{\text{1}}^{\text{2}}}{\text{v}_{\text{1}}^{\text{2}}\text{ - v}_{\text{2}}^{\text{2}}}}$ B. $\sqrt{\frac{\text{v}_{\text{1}}^{\text{2}}\text{x}_{\text{2}}^{\text{2}}\text{ - v}_{\text{2}}^{\text{2}}\text{x}_{\text{1}}^{\text{2}}}{\text{v}_{\text{1}}^{\text{2}}\text{ + v}_{\text{2}}^{\text{2}}}}$ C. $\sqrt{\frac{\text{v}_{\text{1}}^{\text{2}}\text{x}_{\text{2}}^{\text{2}}\text{ - v}_{\text{2}}^{\text{2}}\text{x}_{\text{1}}^{\text{2}}}{\text{v}_{\text{1}}^{\text{2}}\text{ - v}_{\text{2}}^{\text{2}}}}$ D. $\sqrt{\frac{\text{v}_{\text{1}}^{\text{2}}\text{x}_{\text{2}}^{\text{2}}\text{ + v}_{\text{2}}^{\text{2}}\text{x}_{\text{1}}^{\text{2}}}{\text{v}_{\text{1}}^{\text{2}}\text{ + v}_{\text{2}}^{\text{2}}}}$
Câu 17: Một chất điểm dao động điều hòa trên một đoạn thẳng, khi đi qua M và N chất điểm có gia tốc lần lượt là ${{\text{a}}_{\text{M}}}\text{ = 3}\ \text{m/}{{\text{s}}^{\text{2}}}$ và ${{\text{a}}_{\text{N}}}\text{ = 8 m/}{{\text{s}}^{\text{2}}}$. A là một điểm trên đoạn MN và $\text{AM = 3}\text{.AN}$. Gia tốc chất điểm khi đi qua A:
A. $11\text{ m/}{{\text{s}}^{2}}$ B. $5\text{ m/}{{\text{s}}^{2}}$ C. $\text{2,75 m/}{{\text{s}}^{2}}$ D. $6,75\text{ m/}{{\text{s}}^{2}}$
Câu 18: Li độ và tốc độ của một vật dao động điều hòa liên hệ với nhau theo biểu thức $\frac{{{\text{x}}^{\text{2}}}}{36}\text{ + }\frac{{{\text{v}}^{\text{2}}}}{0,09}\text{ = 1}$. Trong đó $\text{x}$ và $\text{v}$ lần lượt tính theo đơn vị $\text{cm}$và $\text{m/s}$. Biên độ dao động của vật là:
A. 6 cm B. 3 cm C. 4 cm D. 5 cm

Câu 20: Hai vật dao động điều hòa dọc theo các trục song song với nhau. Phương trình dao động của các vật lần lượt là ${{\text{x}}_{\text{1}}}\text{ = }{{\text{A}}_{\text{1}}}\text{cos}\left( \text{ }\!\!\omega\!\!\text{ t + }{{\text{ }\!\!\varphi\!\!\text{ }}_{\text{1}}} \right)\ \left( \text{cm} \right)$và $\text{ }{{\text{x}}_{\text{2}}}\text{ = }{{\text{A}}_{\text{2}}}\text{cos}\left( \text{ }\!\!\omega\!\!\text{ t + }{{\text{ }\!\!\varphi\!\!\text{ }}_{\text{2}}} \right)\text{ }\left( \text{cm} \right)$.Biết $\text{3x}_{\text{1}}^{\text{2}}\text{ + 2x}_{\text{2}}^{\text{2}}\text{ = 50 }\left( \text{c}{{\text{m}}^{\text{2}}} \right)$. Tại thời điểm t, vật thứ hai đi qua vị trí có li độ ${{\operatorname{x}}_{2}}=1 cm $với vận tốc ${{\text{v}}_{\text{2}}}\text{ = 15 cm/s}$. Khi đó vật thứ nhất có tốc độ bằng:
A. $\text{5 cm/s}$ B. $\text{5}\sqrt{\text{3}}\text{ cm/s}$ C. $10\ \text{cm/s}$ D. $2,5\ \text{cm/s}$

Đáp án:








