Chuyên Đề Lớp 6: Số Nguyên Tố - Hợp Số - Phân tích một số ra thừa số nguyên tố

Chuyên Đề Lớp 6:

Số Nguyên Tố - Hợp Số - Phân tích một số ra thừa số nguyên tố

I. Lý thuyết:

Định nghĩa:

Số nguyên tố là số tự nhiên lớn hơn 1, chỉ có 2 ước là 1 và chính nó.

Ví dụ : Ư(13) = {13 ; 1} nên 13 là số nguyên tố.

Hợp số là số tự nhiên lớn hơn 1, có nhiều hơn 2 ước.

Cách kiểm tra 1 số là số nguyên tố:

Để kết luận số a là số nguyên tố (a>1), chỉ cần chứng tỏ rằng nó không chia hết cho mọi số nguyên tố mà bình phương không vượt quá a.

Phân tích 1 số ra thừa số nguyên tố:

Phân tích một số tự nhiên lớn hơn 1 ra thừa số nguyên tố là viết số đó dưới dạng một tích các thừa số nguyên tố
Muốn phân tích một số tự nhiên a lớn hơn 1 ra thừa số nguyên tố ta có thể làm như sau:

Kiểm tra xem 2 có phải là ước của a hay không. Nếu không ta xét số nguyên tố 3 và cứ như thế đối với các số nguyên tố lớn dần.
Giả sử p là ước nguyên tố nhỏ nhất của a, ta chia a cho p được thương b.
Tiếp tục thực hiện quy trình trên đối với b.
Quá trình trên kéo dài cho đến khi ta được thương là một số nguyên tố.

Lưu ý: Dù phân tích một số tự nhiên ra thừa số nguyên tố bằng cách nào thì cũng được cùng một kết quả.

Phương pháp giải:

Cách 1 : (Phân tích theo cột dọc) : Chia số n cho một số nguyên tố (xét từ nhỏ đến lớn), rồi chia thương tìm được cho một số nguyên tố (cũng xét từ nhỏ đến lớn), cứ tiếp tục như vậy cho đến khi thương bằng 1.

Ví dụ :

\[90\text{ }=\text{ }{{2.3}^{2}}\text{ }.5\]\[90\text{ }=\text{ }{{2.3}^{2}}\text{ }.5\]

Cách 2 (Phân tích theo hàng ngang hoặc theo “sơ đồ cây”): Viết n dưới dạng một tích các thừa số, mỗi thừa số lại viết thành tích cho đến khi các thừa số đều là sốnguyên tố.

Ví dụ :

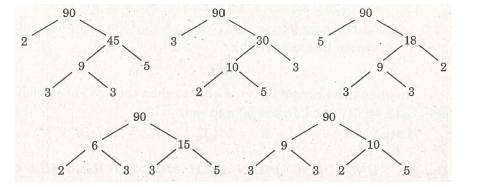
\[90\text{ }=\text{ }9.10\text{ }=\text{ }{{3}^{2}}.2.5.\]Tất cả các cách phân tích số 90 ra thừa số nguyên tố đều cho cùng một kết quả.

Cách tính số lượng các ước của một số m (m > 1):

Ta xét dạng phân tích của số m ra thừa số nguyên tố:

Nếu m = ax thì m có x + 1 ước
Nếu m = ax. by thì m có (x + 1)(y + 1) ước
Nếu m = ax. by. cz thì m có (x + 1)(y + 1)(z + 1) ước.

II. Bài tập ví dụ:

Bài 1: Tổng (hiệu) sau là số nguyên tố hay hợp số:

a/ 3150 + 2125

b/ 5163 + 2532

c/ 19. 21. 23 + 21. 25 .27

d/ 15. 19. 37 – 225

Hướng dẫn

a/ Tổng lớn hơn 5 và chia hết cho 5, nên tổng là hợp số.

b/ Hiệu lớn hơn 3 và chia hết cho 3, nên hiệu là hợp số.

c/ Tổng lớn hơn 21 và chia hết cho 21 nên tổng là hợp số.

d/ Hiệu lớn hơn 15 và chia hết cho 15 nên hiệu là hợp số.

Bài 2: Chứng tỏ rằng các số sau đây là hợp số:

a/ 297; 39743; 987624

b/ 111…1 có 2001 chữ số 1 hoặc 2007 chữ số 1

Hướng dẫn

a/ Các số trên đều chia hết cho 11

Dùng dấu hiệu chia hết cho 11 đê nhận biết: Nếu một số tự nhiên có tổng các chữ số đứng ở vị trí hàng chẵn bằng tổng các chữ số ở hàng lẻ ( số thứ tự được tính từ trái qua phải, số đầu tiên là số lẻ) thì số đó chia hết cho 11. Chẳng hạn 561, 2574,…

b/ Nếu số đó có 2001 chữ số 1 thì tổng các chữ số của nó bằng 2001 chia hết cho 3. Vậy số đó chia hết cho 3. Tương tự nếu số đó có 2007 chữ số 1 thì số đó cũng chia hết cho 9.

Bài 3: Hãy xét xem các số tự nhiên từ 1991 đến 2005 số nào là số nguyên tố?

Hướng dẫn

- Trước hết ta loại bỏ các số chẵn: 1992, 1994, 1996, …, 2004

- Loại bỏ tiếp các số chia hết cho 3: 1995, 2001

- Ta còn phải xét các số 1991, 1993, 1997, 1999, 2003 số nguyên tố p mà \[{{p}^{2}}\]< 2005 là 11, 13, 17, 19, 23, 29, 31, 37, 41, 43.

- Số 1991 chia hết cho 11 nên ta loại.

- Các số còn lại 1993, 1997, 1999, 2003 đều không chia hết cho các số nguyên tố tên.

Vậy từ 1991 đến 2005 chỉ có 4 số nguyên tố là 1993, 1997, 1999, 2003

Bài 4: Phân tích các số 120, 900, 100000 ra thừa số nguyên tố

ĐS:

Bài 5:

a/ Số tự nhiên khi phân tích ra thừa số nguyên tố có dạng \[{{2}^{2}}\text{ }.\text{ }{{3}^{3}}.\]Hỏi số đó có bao nhiêu ước?\[{{p}_{1}}^{k}.\text{ }{{p}_{2}}^{l.}\text{ }{{p}_{3}}^{m}\]

b/ A = \[{{p}_{1}}^{k}.\text{ }{{p}_{2}}^{l.}\text{ }{{p}_{3}}^{m}\]\[\]có bao nhiêu ước?

Hướng dẫn

a/ Số đó có (2+1).(3+1) = 3. 4 = 12 (ước).

b/ A = \[{{p}_{1}}^{k}.\text{ }{{p}_{2}}^{l.}\text{ }{{p}_{3}}^{m}\]có (k + 1).(l + 1).(m + 1) ước

Ghi nhớ: Người ta chứng minh được rằng: “Số các ước của một số tự nhiên a bằng một tích mà các thừa số là các số mũ của các thừa số nguyên tố của a cộng thêm 1”

a = \[{{p}^{k}}{{q}^{m}}\ldots {{r}^{n}}\]Số phần tử của Ư(a) = (k+1)(m+1)…(n+1)

III. Bài tập luyện tập:

Bài 1: Phân tích các thừa số sau thành tích các thừa số nguyên tố.

a) 27 ; 30 ; 80 ; 20 ; 120 ; 90. c) 16 ; 48 ; 98 ; 36 ; 124.

b ) 15 ; 100 ; 112 ; 224 ; 184. d) 56 ; 72 ; 45 ; 54 ; 177

Bài 2: Tìm hai số nguyên tố biết tổng của chúng bằng 601.

Bài 3: Tổng của 3 số nguyên tố bằng 1012. Tìm số nhỏ nhất trong 3 số đó.

Bài 4:Cho A = \[5\text{ }+\text{ }{{5}^{2\text{ }}}+\text{ }{{5}^{3}}\text{ }+...+\text{ }{{5}^{100}}\]

a) Số A là số nguyên tố hay hợp số?

b) Số A có phải là số chính phương không?

Bài 5:Tổng (hiệu) sau là số nguyên tố hay hợp số?

a) 1.3.5.7.13 + 20