Con Lắc Đơn

CON LẮC ĐƠN

 

I. KHẢO SÁT DAO ĐỘNG ĐIỀU HÒA CỦA CON LẮC ĐƠN

1. Khảo sát dao động điều hòa của con lắc đơn

Xét con lắc đơn gồm vật nặng có khối lượng m và dây treo có chiều dài l. Kéo vật lên ra khỏi vị trí cân bằng một góc α0 rồi thả nhẹ cho vật dao động, cho rằng trong quá trình dao động của vật các lực cản có độ lớn không đáng kể, có thể bỏ qua: Phương trình định luật II Niuton cho vật: \[\overrightarrow{P}+\overrightarrow{T}=m\overrightarrow{a}\] Chiếu lên phương của quỹ đạo chiều dương hướng từ trái sang phải, ta thu được phương trình đại số: \[-mg\sin \alpha =m{{a}_{t}}\] Trong tường hợp con lắc dao động với li độ góc nhỏ, khi đó: \[\sin \alpha \approx \alpha =\frac{s}{l}\] Thay vào biểu thức trên: \[{s}''+\frac{g}{l}s=0\]

Phương trình này cho nghiệm dưới dạng:

\[s={{s}_{0}}\cos \left( \omega t+{{\varphi }_{0}} \right)\] trong đó \[{{\omega }^{2}}=\frac{g}{l}\]

Từ mối liên hệ \[s=l\alpha \] ta cũng có phương trình tương đương: \[\alpha ={{\alpha }_{0}}\cos \left( \omega t+{{\varphi }_{0}} \right)\]

Các kết quả trên cho thấy rằng, dao động nhỏ của con lắc đơn là dao động điều hòa với chu kì \[T=2\pi \sqrt{\frac{l}{g}}\]

2. Vận tốc của con lắc:

Trong quá trình dao động của con lắc, vận tốc luôn tiếp tuyến với quỹ đạo và được tính bằng đạo hàm bất nhất theo thời gian của li độ cong

\[v={s}'=-\omega {{s}_{0}}\sin \left( \omega t+{{\varphi }_{0}} \right)=\omega {{s}_{0}}\cos \left( \omega t+{{\varphi }_{0}}+\frac{\pi }{2} \right)\]

\[\Rightarrow \]Công thức độc lập thời gian giữa vận tốc và li độ cong:

\[{{\left( \frac{s}{{{s}_{0}}} \right)}^{2}}+{{\left( \frac{v}{\omega {{s}_{0}}} \right)}^{2}}=1\]

3. Gia tốc dao động điều hòa (tiếp tuyến) của con lắc:

Gia tốc của con lắc được tính bằng đạo hàm bậc hai theo thời gian của li độ cong:

\[a={s}''=-{{\omega }^{2}}{{s}_{0}}\cos \left( \omega t+{{\varphi }_{0}} \right)=-{{\omega }^{2}}s={{\omega }^{2}}{{s}_{0}}\cos \left( \omega t+{{\varphi }_{0}}+\pi  \right)\]

\[\Rightarrow \]Công thức độc lập thời gian giữa gia tốc và vận tốc:

\[{{\left( \frac{v}{\omega {{s}_{0}}} \right)}^{2}}+{{\left( \frac{a}{{{\omega }^{2}}{{s}_{0}}} \right)}^{2}}=1\]

Sử dụng công thức liên hệ \[s=l\alpha \]ta cũng có được các công thức tương tự

 

II. NĂNG LƯỢNG CỦA CON LẮC ĐƠN TRONG DAO ĐỘNG ĐIỀU HÒA:

Chọn mốc thế năng của vật tại vị trí cân bằng. Cơ năng của vật trong quá trình dao động điều hòa bằng tổng động năng và thế năng của vật: \[\text{W}={{\text{W}}_{d}}+{{\text{W}}_{t}}=\frac{m{{v}^{2}}}{2}+mgl\left( 1-\cos \alpha  \right)\] Vì cơ năng của vật được bảo toàn nên cơ năng chính bằng thế năng cực đại của vật, ứng với vị trí có li độ góc \[\alpha ={{\alpha }_{0}}\] \[\text{W}=mgl\left( 1-\cos {{\alpha }_{0}} \right)\] Với trường hợp dao động bé, góc α0 nhỏ ta có công thức gần đúng \[\text{W}=\frac{1}{2}mgl\alpha _{0}^{2}\]

III. TỐC ĐỘ, GIA TỐC VÀ LỰC CĂNG DÂY

1. Tốc độ:

Từ định luật bảo toàn cơ năng ta có cơ năng của con lắc tại vị trí có li độ góc α luôn bằng thế năng cực đại \[mgl\left( 1-\cos {{\alpha }_{0}} \right)=\frac{m{{v}^{2}}}{2}+mgl\left( 1-\cos \alpha  \right)\] Suy ra: \[v=\sqrt{2gl\left( \cos \alpha -\cos {{\alpha }_{0}} \right)}\] Từ biểu thức trên chúng ta có thể suy ra được rằng: + Vật đạt tốc độ cực đại khi đi qua vị trí cân bằng \[\alpha =0\Rightarrow {{v}_{\max }}=\sqrt{2gl\left( 1-\cos {{\alpha }_{0}} \right)}\] + Vật đạt tốc độ cực tiểu khi đi qua vị trí biên \[\alpha ={{\alpha }_{0}}\Rightarrow {{v}_{\min }}=0\]

2. Gia tốc:

Gia tốc của con lắc trong quá trình chuyển động:\[a=\sqrt{a_{n}^{2}+a_{t}^{2}}\]

+ \[{{a}_{t}}\]: là gia tốc tiếp tuyến của vật, đặc trưng cho sự thay đổi của vận tốc về độ lớn

+ \[{{a}_{n}}\]: là gia tốc pháp tuyến (hướng tâm) của vật, đặc trưng cho sự thay đổi của vận tốc về phương chiều

Ta có:

+ \[{{a}_{n}}=\frac{{{v}^{2}}}{l}=2g\left( \cos \alpha -\cos {{\alpha }_{0}} \right)\]

+ \[{{a}_{t}}={s}''\] hoặc ta có thể dùng \[{{a}_{t}}=g\sin \alpha \]

Từ các kết quả trên ta có thể suy ra rằng:

+ Khi vật ở vị trí cân bằng ứng với giá trị li độ góc \[\alpha =0\]:

\[{{a}_{t}}=0\], \[{{a}_{n}}={{a}_{n\max }}=2g\left( 1-\cos {{\alpha }_{0}} \right)\] và \[a={{a}_{n}}\]

+ Khi vật ở vị trí biên ứng với giá trị li độ góc \[\alpha ={{\alpha }_{0}}\]:

\[{{a}_{t}}={{a}_{t\max }}=g\sin {{\alpha }_{0}}\], \[{{a}_{n}}=0\] và \[a={{a}_{t}}\]

 

3. Lực căng dây:

Phương trình định luật II Niuton cho vật: \[\overrightarrow{T}+\overrightarrow{P}=m\overrightarrow{a}\] Chiếu lên phương hướng tâm ta thu được phương trình đại số: \[T-P\cos \alpha =m{{a}_{n}}\] Với \[{{a}_{n}}=\frac{{{v}^{2}}}{l}=2g\left( \cos \alpha -\cos {{\alpha }_{0}} \right)\] Biến đổi toán học ta thu được biểu thức của lực căng dây: \[T=mg\left( 3\cos \alpha -2\cos {{\alpha }_{0}} \right)\] Từ biểu thức trên ta cũng có thể suy ra rằng: + Khi vật ở vị trí cân bằng ứng với giá trị li độ góc \[\alpha =0\]: \[T={{T}_{\max }}=mg\left( 3-2\cos {{\alpha }_{0}} \right)\] + Khi vật ở vị trí biên ứng với giá trị li độ góc \[\alpha ={{\alpha }_{0}}\]: \[T={{T}_{\min }}=mg\cos {{\alpha }_{0}}\]

B: BÀI TẬP MẪU

Hướng dẫn

Chu kì dao động của con lắc đơn \[T=2\pi \sqrt{\frac{l}{g}}\] với \[g=\frac{P}{m}\] là tỉ số giữa trọng lượng và khối lượng của con lắc

• Đáp án C

 

Hướng dẫn

\[{{\text{W}}_{d}}={{\text{W}}_{t}}\] và \[{{\text{W}}_{d}}+{{\text{W}}_{t}}=\text{W}\] \[\Rightarrow 2{{W}_{t}}=\text{W}\Rightarrow \alpha =\pm \frac{{{\alpha }_{0}}}{\sqrt{2}}\]

Vật đang chuyển động nhanh dần đều theo chiều dương, do đó \[\alpha =-\frac{{{\alpha }_{0}}}{\sqrt{2}}\]

• Đáp án C

 

Hướng dẫn

Từ công thức độc lập thời gian giữa vận tốc và li độ cong, ta có:

\[\left| v \right|=\omega \sqrt{s_{0}^{2}-{{s}^{2}}}=\omega l\sqrt{\alpha _{0}^{2}-{{\alpha }^{2}}}=\frac{2\pi }{T}l\sqrt{\alpha _{0}^{2}-{{\alpha }^{2}}}=4\pi \]cm/s

• Đáp án C

 

Hướng dẫn

Theo giả thuyết bài toán, ta có:

\[v=\frac{1}{2}{{v}_{ma\text{x}}}\Leftrightarrow \sqrt{2gl\left( \cos \alpha -\cos {{\alpha }_{0}} \right)}=\frac{1}{2}\sqrt{2gl\left( 1-\cos {{\alpha }_{0}} \right)}\Leftrightarrow \cos \alpha -\cos {{\alpha }_{0}}=\frac{1-\cos {{\alpha }_{0}}}{4}\xrightarrow{Sjift\to Solve}\alpha ={{51,3}^{0}}\]

• Đáp án A

 

Hướng dẫn

Từ biểu thức của lực căng dây \[T=mg\left( 3\cos \alpha -2\cos {{\alpha }_{0}} \right)\]

+ Tại vị trí cân bằng \[\alpha =0\Rightarrow T=mg\left( 3-2\cos {{\alpha }_{0}} \right)\ne P=mg\]

• Đáp án C

 

Hướng dẫn

Tỉ số giữa lực căng dây cực đại và cực tiểu

\[\frac{{{T}_{ma\text{x}}}}{{{T}_{\min }}}=\frac{1+\alpha _{0}^{2}}{1-\frac{\alpha _{0}^{2}}{2}}=1,02\xrightarrow{shift\to Solve}{{\alpha }_{0}}=0,115\text{rad}={{6,6}^{0}}\]

• Đáp án A

 

C: BÀI TẬP TỰ LUYỆN

Câu 7: Một con lắc đơn có chiều dài dây treo 43,2 cm, vật có khối lượng m dao động ở nơi có gia tốc trọng trường \[g=10\]m/s². Biết rằng độ lớn của lực căng dây cực đại bằng 4 lần độ lớn lực căng dây cực tiểu. Tốc độ của vật khi lực căng dây bằng 2 lần lực căng dây cực tiểu:

          A. 1 m/s                       B. 1,2 m/s                    C. 1,6 m/s     D. 2 m/s

Câu 8: Một con lắc đơn có dây treo dài 0,4 m và vật nặng có khối lượng 200 g. Lấy \[g=10\]m/s² và bỏ qua ma sát. Kéo con lắc để dây treo lệch ra khỏi vị trí cân bằng 60⁰ rồi thả nhẹ. Lúc lực căng dây có độ lớn là 4 N thì tốc độ của vật là:

          A. \[\sqrt{2}\]m/s         B. \[2\sqrt{2}\]m/s        C. 5 m/s     D. 2 m/s

Câu 9: Một con lắc đơn gồm vật nặng có khối lượng 100 g, dao động điều hòa với chu kì 2 s. Khi vật đi qua vị trí cân bằng thì lực căng dây có độ lớn 1,0025 N. Chọn mốc thế năng tại vị trí cân bằng, lấy \[g={{\pi }^{2}}\]m/s². Cơ năng của vật là:

          A. \[{{25.10}^{-3}}\] J                                    B. \[{{25.10}^{-4}}\]J                C. \[{{125.10}^{-5}}\]J           D. \[{{125.10}^{-4}}\]J

Câu 10: Con lắc đơn dao động điều hòa, khi tăng chiều dài của con lắc lên 4 lần thì tần số dao động của con lắc sẽ:

          A. giảm đi 4 lần                                                B. tăng lên 4 lần

          C. giảm đi 2 lần                                                D. tăng lên 2 lần

Câu 11: Tại một nơi, con lắc đơn có chiều dài l₁ dao động điều hoà với tần số f₁; con lắc đơn có chiều dài \[{{l}_{2}}=2{{l}_{1}}\] dao động điều hoà với tần số f₂. Hệ thức đúng là

          A. \[\frac{{{f}_{1}}}{{{f}_{2}}}=\frac{1}{\sqrt{2}}\]           B. \[\frac{{{f}_{1}}}{{{f}_{2}}}=\frac{1}{2}\]           C. \[\frac{{{f}_{1}}}{{{f}_{2}}}=\frac{\sqrt{2}}{1}\] D. \[\frac{{{f}_{1}}}{{{f}_{2}}}=\frac{2}{1}\]

Câu 12: Tại một nơi có gia tốc trọng trường g, một con lắc đơn dao động điều hòa với biên độ α₀. Biết vật có khối lượng m và dây dài l. Cơ năng của con lắc là:

          A. \[\frac{1}{2}mgl\alpha _{0}^{2}\]              B. \[mgl\alpha _{0}^{2}\]           C. \[\frac{1}{4}mgl\alpha _{0}^{2}\]            D. \[\frac{1}{4}mgl\alpha _{0}^{2}\]

Câu 13: Treo một con lắc đơn tại nơi có gia tốc \[g={{\pi }^{2}}\]m/s², chiều dài của dây treo là 1 m và bỏ qua tác dụng của lực cản. Kéo vật lệch ra khỏi vị trí cân bằng một góc 6⁰ rồi thả nhẹ cho vật dao động điều hòa. Chọn gốc thời gian là lúc buông vật, chiều dương là chiều chuyển động của vật ngay khi buông vật. Phương trình dao động của vật nhỏ là:

          A. \[s=\frac{\pi }{30}\cos \left( \pi t+\pi  \right)\]m                                                                    B. \[s=\frac{\pi }{30}\cos \left( \pi t \right)\]m

          C. \[s=0,06\cos \left( \pi t \right)\]m                                                                    D. \[s=0,06\cos \left( \pi t+\pi  \right)\]m

Câu 14: Một con lắc đơn có chiều dài dây treo bằng 40 cm, khối lượng của vật nặng bằng 10 g. Vật dao động với biên độ góc \[{{\alpha }_{0}}=0,1\]rad tại nơi có gia tốc trọng trường \[g=10\]m/s². Vận tốc của vật khi đi qua vị trí cân bằng là:

          A. \[\pm \]0,2 m/s         B. \[\pm 0,4\]m/s          C. \[\pm 0,1\]m/s               D. \[\pm 0,3\]m/s

Câu 15: Tại nơi có gia tốc trọng trường \[g=9,8\]m/s² một con lắc đơn dao động điều hòa với chu kì \[\frac{2\pi }{7}\] s và biên độ góc \[{{\alpha }_{0}}=0,1\]rad. Vật dao động với biên độ dài:

          A. 1 m                          B. 10 cm                      C. 15 cm      D. 2 cm

Câu 16: Trong khoảng thời gian Δt một con lắc có chiều dài l thực hiện được 12 dao động toàn phần. Nếu giảm chiều dài của con lắc 16 cm thì trong khoảng thời gian trên nó thực hiện được 20 dao động toàn phần. Giá trị của l là:

          A. 20 cm                      B. 25 cm                      C. 40 cm      D. 50 cm

Câu 17: Con lắc đơn dao động điều hòa theo thời gian có ly độ góc mô tả theo hàm cosin với biên độ góc a₀, tần số góc w và pha ban đầu j. Chiều dài giây treo là l. Phương trình ly độ góc biến thiên theo thời gian có dạng

A. \[\alpha ={{\alpha }_{0}}\cos \left( \omega t+\varphi  \right)\]                                   B. \[\alpha =\omega {{\alpha }_{0}}\cos \left( \omega t+\varphi  \right)\]                

C. \[\alpha ={{\omega }^{2}}{{\alpha }_{0}}\cos \left( \omega t+\varphi  \right)\]                   D. \[\alpha =l{{\alpha }_{0}}\cos \left( \omega t+\varphi  \right)\]

Câu 18: Một con lắc đơn có chiều dài dây treo là l, dao động điều hòa tại nơi có gia tốc trọng trường g với chu kì:

          A. \[\pi \frac{g}{l}\]     B. \[2\pi \sqrt{\frac{l}{g}}\]                 C. \[2\pi \sqrt{\frac{g}{l}}\]                 D. \[\sqrt{\frac{l}{g}}\]

Câu 19: Một con lắc đơn có chiều dài dây treo l₁ dao động với biên độ góc nhỏ và chu kì dao động \[{{T}_{1}}=0,6\text{s}\]. Con lắc đơn có chiều dài l₂ có chu kì dao động cũng tại nơi đó \[{{T}_{2}}=0,8\text{s}\]. Chu kì của con lắc có chiều dài \[l={{l}_{1}}+{{l}_{2}}\] là

          A. 0,48 s                      B. 1,0 s                        C. 0,7 s         D. 1,4 s

Câu 20: Một con lắc đơn có chiều dài l, dao động điều hoà tại một nơi có gia tốc rơi tự do g với biên độ góc \[{{\alpha }_{0}}\].  Lúc vật đi qua vị trí có li độ x\[\alpha \] , nó có vận tốc là v. Biểu thức nào sau đây đúng?

A. \[{{\alpha }^{2}}=\alpha _{0}^{2}-\frac{{{v}^{2}}g}{l}\]

B. \[\frac{{{v}^{2}}g}{l}=\alpha _{0}^{2}-{{\alpha }^{2}}\]

C. \[\alpha _{0}^{2}={{\alpha }^{2}}+\frac{{{v}^{2}}g}{l}\]                                

D. \[{{\alpha }^{2}}=\alpha _{0}^{2}-gl{{v}^{2}}\]

Câu 21: Một con lắc đơn dao động điều hòa. Dây treo có độ dài không đổi. Nếu đặt con lắc tại  nơi có gia tốc rơi tự do là g₀ thì chu kỳ dao động là 1s.  Nếu đặt con lắc tại nơi có gia tốc rơi tự do là g thì chu kỳ dao động là

A. $\frac{{{g}_{0}}}{g}$s.           B. $\frac{g}{{{g}_{0}}}$s.      

C. $\sqrt{\frac{{{g}_{0}}}{g}}$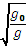 s.           D. $\sqrt{\frac{g}{{{g}_{0}}}}$ 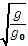s.

Câu 22: Một con lắc đơn đang dao động điều hòa với biên độ góc α₀ dưới tác dụng của trọng lực. Ở thời điểm t₀, vật nhỏ của con lắc có li độ góc α và tốc độ dài v. Lấy \[g=10\text{ }\]m/s². Li độ cong của con lắc tại thời điểm t₀ được xác định theo công thức

A. \[s=\frac{l\alpha {{v}^{2}}}{g\left( \alpha _{0}^{2}-{{\alpha }^{2}} \right)}\]                    

B. \[s=\frac{\alpha {{v}^{2}}}{g\left( \alpha _{0}^{2}-{{\alpha }^{2}} \right)}\]                    

C. \[s=\frac{\alpha {{v}^{2}}}{g\left( {{\alpha }^{2}}-\alpha _{0}^{2} \right)}\]                

D. \[s=\frac{{{v}^{2}}}{g\left( \alpha _{0}^{2}-{{\alpha }^{2}} \right)}\]

Câu 23: (Minh họa – 2017) Một con lắc đơn có chiều dài 1 m, được treo tại nơi có gia tốc trọng trường g = π² m/s². Giữ vật nhỏ của con lắc ở vị trí có li độ góc −9^o rồi thả nhẹ vào lúc t = 0. Phương trình dao động của vật là

          A. \[s=5\cos \left( \pi t+\pi  \right)\]cm                                                                  B. \[s=5\cos \left( 2\pi t \right)\]cm

          C. \[s=5\pi \cos \left( \pi t+\pi  \right)\]cm                                                                  D. \[s=5\pi \cos \left( 2\pi t \right)\]cm

Câu 24: (Quốc gia – 2010) Tại nơi có gia tốc trọng trường g, một con lắc đơn dao động điều hòa với biên độ góc a₀ nhỏ. Lấy mốc thế năng ở vị trí cân bằng. Khi con lắc chuyển động nhanh dần theo chiều dương đến vị trí có động năng bằng thế năng thì li độ góc a của con lắc bằng

          A. \[\frac{{{\alpha }_{0}}}{\sqrt{3}}\]           B. \[\frac{{{\alpha }_{0}}}{\sqrt{2}}\]                          C. \[-\frac{{{\alpha }_{0}}}{\sqrt{2}}\]                             D. \[-\frac{{{\alpha }_{0}}}{\sqrt{3}}\]

Câu 25: Một con lắc đơn có chiều dài dây treo l = 2m dao động điều hòa trọng trường biên độ góc \[{{\alpha }_{0}}=0,175\] rad . Chọn mốc thế năng của vật tại vị trí cân bằng. Ở vị trí tại đó vật có động năng bằng ba lần thế năng thì chiều dài cung tính từ vị trí cân bằng đến vị trí của vật gần bằng

          A. 22,5 cm                   B. 30,0 cm                   C. 17,5 cm      D. 25,0 cm

Câu 26: Chọn phát biểu sai. Xét con lắc đơn dao động điều hòa dưới tác dụng của trọng lực và lực căng dây, chu kì dao động của con lắc sẽ thay đổi khi

          A. giảm chiều dài của dây treo và giữa nguyên các thông số khác

          B. tăng chiều dài của dây treo và giữa nguyên các thông số khác

          C. thay đổi gia tốc trọng trường tại nơi đặt con lắc và giữ nguyên các thông số khác

          D. thay đổi khối lượng của vật nặng và giữ nguyên các thông số khác

Câu 27: Một con lắc đơn dao động điều hòa với phương trình dao động \[s=7,2\cos \left( \frac{5\pi }{6}t-\frac{\pi }{3} \right)cm\]. Lấy \[g={{\pi }^{2}}\]cm/s². Biên độ góc của dao động

          A. 0,069 rad                 B. 0,072 rad                 C. 0,05 rad            D. 0,036 rad

 

ĐÁP ÁN

7.B	8.D	9.C	10.C	11.C	12.A	13.A	14.A	15.D	16.B
17.A	18.B	19.B	20.C	21.C	22.C	23.C	24.C	25.C	26.D

Bài viết gợi ý: