I. TÓM TẮT LÍ THUYẾT
1.Khái niệm con lắc đơn.
_Con lắc đơn gồm một vật nhỏ, khối lượng m, treo ở đầu một sợi dây mềm không dãn, khối lượng không đáng kể, dài l.
- Trong hệ quy chiếu quán tính, vị trí cân bằng của con lắc đơn là vị trí dây treo có phương thẳng đứng, vật nặng ở vị trí thấp nhất.
- Khi dao động của con lắc đơn với góc lệch nhỏ ( sinα$\approx \alpha$(rad)), con lắc dao động điều hoà
với chu kỳ:$T=2\pi \sqrt{\frac{l}{g}}$
Trong đó:l là chiều dài của con lắc (đơn vị là mét); g là gia tốc trọng trường tại vị trí đặt con lắc ( đơn vị m/s2).
2. Con lắc đồng hồ.
- Đồng hồ quả lắc có con lắc làm bằng thanh kim loại mảnh và dao động của con lắc có thể coi như dao động điều hoà của con lắc đơn.
- Chu kỳ chạy đúng của đồng hồ là T (thường T =2s); trong một số trường hợp do nhiệt độ môi trường thay đổi và vị trí đặt con lắc thay đổi nên đồng hồ chạy sai. Gọi chu kỳ chạy sai của đồng hồ là T2 (còn chu kỳ chạy đúng T =T1) và độ biến thiên chu kỳ là $\Delta $T = T2 – T1. Nếu:
+ $\Delta $T> 0: T2 > T1: Chu kỳ tăng, đồng hồ chạy chậm.
+ $\Delta $T< 0: T2 < T1 :Chu kỳ giảm, đồng hồ chạy nhanh.
+ $\Delta $T= 0. Chu kỳ không đổi, con lắc chạy đúng.
- Thời gian con lắc đồng hồ chạy sai sau khoảng thời gian$\tau $:
+ Thời gian biểu kiến con lắc chạy sai chỉ là: ${{\tau }^{'}}=n{{T}_{1}}$.
Với n là số chu kỳ con lắc chạy sai T2 trong khoảng thời gian$\tau $: $n=\frac{\tau }{{{T}_{2}}}$.
+ Thời gian chạy sai: 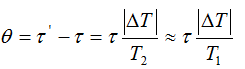
Nếu T2 thay đổi không đáng kể so với T1 thì 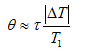
II. CÁC DẠNG BÀI TOÁN VÀ PHƯƠNG PHÁP GIẢI
Dạng 1: Chu kỳ con lắc đơn thay đổi theo chiều dài l.
Ví dụ 1: Con lắc đơn chiều dài l1 dao động điều hoà tại một nơi với chu kỳ T1 = 1,5s. Con lắc đơn chiều dài l2 cũng dao động điều hoà tại nơi đó với chu kỳ T2 =0,9s. Tính chu kỳ của con lắc chiều dài l dao động điều hoà ở nơi trên với:
l = l1+l2 và l = l1- l2
Hướng dẫn:
-Với l = l1+l2 Sử dụng công thức $T=\sqrt{T_{1}^{2}+T_{2}^{2}}$
Thay số: $T=\sqrt{1,{{5}^{2}}+0,{{9}^{2}}}=1,75s$
-Với l = l1- l2 Sử dụng công thức $T=\sqrt{T_{1}^{2}-T_{2}^{2}}$
Thay số: $T=\sqrt{1,{{5}^{2}}-0,{{9}^{2}}}=1,2s$
Ví dụ 2:
Một con lắc đơn có dây treo chiều dài l. Người ta thay đổi độ dài của nó tới giá trị l’ sao cho chu kỳ dao động mới chỉ bằng 90% chu kỳ dao động ban đầu. Hỏi chiều dài l’ bằng bao nhiêu lần chiều dài l ?
Hướng dẫn: Chu kỳ con lắc chiều dài l và l’ lần lượt là:
${{T}_{1}}=2\pi \sqrt{\frac{l}{g}}$ và ${{T}_{2}}=2\pi \sqrt{\frac{{{l}^{'}}}{g}}$
Tỷ số: $\frac{{{T}_{2}}}{{{T}_{1}}}=\sqrt{\frac{{{l}^{'}}}{l}}=90%=0,9$ $\Rightarrow {{l}^{'}}=0,81l$
Ví dụ 3:
Một đồng hồ quả lắc chạy đúng giờ vào mùa nóng khi nhiệt độ trung bình là 320c, con lắc có thể xem là con lắc đơn. Hệ số nở dài của dây treo con lắc
$\alpha $ = 2.10-5K-1. Vào mùa lạnh nhiệt độ trung bình là 170c hỏi con lắc sẽ chạy như thế nào? Một tuần nó chay sai bao nhiêu?
Hướng dẫn: Do nhiệt độ vào mùa đông giảm nên chu kỳ con lắc giảm, đồng hồ chạy nhanh. Một tuần :$\tau $ = 7.24.60.60 s đồng hồ chạy nhanh một thời gian: $\theta =\tau \frac{\left| \Delta T \right|}{{{T}_{1}}}=\tau \frac{1}{2}\alpha \Delta t$ = 7.24.3600.1/2.2.10-5 .15 = 90,72 s.
Ví dụ 4: Con lắc đồng hồ có dây treo làm bằng thanh kim loại mảnh. khi nhiệt độ môi trường tăng thêm 100c thì trong 12 giờ con lắc chạy chậm 30s. Nếu muốn con lắc chạy mỗi ngày chỉ chậm 45s thì nhiệt độ môi trường phải tăng lên bao nhiêu? Coi gia tốc trọng trường không thay đổi.
Hướng dẫn:
Vận dụng công thức: $\theta =\tau \frac{\left| \Delta T \right|}{{{T}_{1}}}=\tau \frac{1}{2}\alpha \Delta t$
Khi nhiệt độ tăng thêm300c thì mỗi ngày sẽ chạy chậm: \[{{\theta }_{1}}=\frac{1}{2}\alpha \Delta {{t}_{1}}=60s\];
Nếu con lắc chạy chậm mỗi ngày 45s thì nhiệt độ tăng lên \[\Delta {{t}_{2}}\] thoả mãn: \[{{\theta }_{2}}=\frac{1}{2}\alpha \Delta {{t}_{2}}=45s\Rightarrow \Delta {{t}_{2}}=3/4\Delta {{t}_{1}}=11,{{25}^{0}}c\]
Ví dụ 5.
Một con lắc đơn dao động nhỏ với chu kỳ T.Nếu chu kỳ của con lắc bị giảm 1% so với giá trị lúc đầu thì chiều dài của con lắc sẽ thay đổi như thế nào? Bằng bao nhiêu phần trăm so với chiều dài ban đầu?
Hướng dẫn:
Vì chu kỳ tỷ lệ thuận với căn bậc hai chiều dài nên chu kỳ giảm chiều gài cũng giảm:
Vận dụng công thức :\[\frac{\Delta T}{T}=\frac{\Delta l}{2l}=0,01\Rightarrow \frac{\Delta l}{l}=0,02\]
Vậy chiều dài con lắc giảm 2%.
Dạng 2: Chu kỳ con lắc đơn thay đổi theo gia tốc trọng trường g.
Ví dụ 1:
Một đồng hồ quả lắc chạy đúng giờ trên mặt đất với chu kỳ T =2s. Đưa con lắc lên độ cao h=1km so với mặt đất và coi như nhiệt độ ở độ cao đó không đôi so với mặt đất.
a/ Xác định chu kỳ của con lắc tại độ cao đó? Cho bán kính trái đất R= 6370 km.
b/ Tại độ cao h con lắc chạy nhanh hay chậm , mỗi ngày chạy sai bao nhiêu?
Hướng dẫn:
a/Chu kỳ của đồng hồ ở độ cao h: ${{T}_{2}}=(1+\frac{h}{R}){{T}_{1}}$
Thay số: ${{T}_{2}}=(1+\frac{1}{6370}).2$=2.00013 s.
b/Chu kỳ tăng, đồng hồ chạy chậm:
$\theta =\tau \frac{\left| \Delta T \right|}{{{T}_{1}}}=\tau \frac{h}{R}=24.3600.\frac{1}{6370}$= 13,569 s
Ví dụ 2:
Một con lắc đơn có chu kỳ dao động nhỏ tại mặt đất là T= 2s. Đưa con lắc xuống giếng sâu 100m so với mặt đất thì chu kỳ của con lắc là bao nhiêu ? Coi trái đất như một hình cầu đồng chất bán kính R = 6400km và nhiệt độ trong giếng không thay đổi so với nhiệt độ trên mặt đất.
Hướng dẫn:
Vận dụng công thức: ${{T}_{2}}=(1+\frac{h}{2R}){{T}_{1}}=(1+\frac{0,1}{2.6400})=2,0000156s$
Chu kỳ con lắc dưới giếng tăng lên so với con lắc đặt trên mặt đất.
Ví dụ 3:
Một đồng hồ quả lắc chạy đúng giờ tren mặt ‘đất. Đưa đồng hồ lên cao 320m so với mặt đất thấy đồng hồ chạy chậm. Đưa đồng hồ xuống hầm mỏ sâu h’ so với mặt đất lại thấy đồng hồ chạy giống ở độ cao h.
a/ Xác định độ sâu của hầm mỏ? Coi nhiệt độ không thay đổi .
b/ Sau một tuần thì đồng hồ chạy sai bao nhiêu thời gian? Coi trái đất hình cầu đồng chât bán kính R = 6400km.
Giải:
a/ Gọi chu kỳ chạy đúng của đồng hồ là T1; chu kỳ ở độ cao h và ở hầm mỏ là T2 và T2’. $\Rightarrow $ T2 = T2’ $\Rightarrow \frac{\Delta T}{{{T}_{1}}}=\frac{\Delta T}{{{T}_{1}}}$
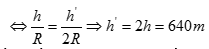
b/ Thời gian đồng hồ chạy chậm sau 1 tuần :
Vận dụng công thức: $\theta =\tau \frac{\left| \Delta T \right|}{{{T}_{1}}}=\tau \frac{h}{2R}=7.24.3600.\frac{0,64}{2.6400}=30,24s$
Ví dụ 4.
Một đồng hồ quả lắc chạy đúng giờ tại Hà Nội (T = 2s). Đưa con lắc vào Hồ Chí Minh giả sử nhiệt độ không thay đổi, Biết gia tốc ở Hà Nội và Hồ Chí Minh lần lượt là: g1 = 9,793m/s2 và g2= 9,787m/s2.
a/ Hãy xác định chu kỳ của con lắc tại Hồ Chí Minh?
b/ Tại Hồ Chí Minh con lắc chạy nhanh hay chậm? Sau 12giờ nó chạy sai bao nhiêu thời gian?
Hướng dẫn:
a/ $\Delta g$= g2-g1 = 9,787 – 9,793 = -0,006.
Sử dung công thức: ${{T}_{2}}=(1-\frac{\Delta g}{2{{g}_{1}}}){{T}_{1}}$ Thay số T2 = 2,006 s.
b/ Chu kỳ tăng nên đồng hồ chạy chậm. Thời gian con lắc chạy chậm trong một ngày đêm: $\theta =\tau \frac{\left| \Delta T \right|}{{{T}_{1}}}=\tau \frac{\Delta g}{2{{g}_{1}}}=12.3600.\frac{0,006}{2.9,793}=13,23s$
Dạng 3:Thay đổi đồng thời cả chiều dài l và gia tốc trọng trường g.
Ví dụ1:
Một con lắc đồng hồ được coi như một con lắc đơn nó chạy đúng ở ngang mực nước biển, nhiệt độ 200c. Đưa con lắc lên độ cao h = 3.2km, nhiệt độ
-100c thì nó chạy nhanh hay chạy chậm? Mỗi ngày chạy sai bao nhiêu biết hệ số nở dài của con lắc là $\alpha $= 1,8.10-5K-1. Bán kính trái đất R = 6400 km.
Hướng dẫn: Sử dụng CT:
$\frac{\Delta T}{{{T}_{1}}}=\frac{1}{2}\alpha \Delta t+\frac{h}{R}=\frac{1}{2}.1,{{8.10}^{-5}}(-10-20)+\frac{3,2}{6400}=2,{{3.10}^{-4}}>0$
Vậy đồng hồ chạy chậm.
Thời gian chạy chậm sau một ngày đêm:
$\theta =\tau \frac{\left| \Delta T \right|}{{{T}_{1}}}=\tau (\frac{1}{2}\alpha \Delta t+\frac{h}{R})=24.3600.2,{{3.10}^{-4}}=19,87s$
Ví dụ 2:
Một con lắc đồng hồ ( xem như con lắc đơn) chạy đúng với chu kỳ T =2 s tại mặt đất có nhiệt độ 250c. Dây treo con lắc làm bằng kim loại có hệ số nở dài $\alpha $= 2.10-5K-1.
a/ Đưa con lắc lên độ cao 1,5km so với mặt đất con lắc lại chạy nhanh hay chạy chậm? Một tuần chạy sai bao nhiêu? Coi nhiệt độ vẫn là 250c.Cho biết bán kính trái đất R = 6400km.
b/ ở độ cao h=1,5km, muốn đồng hồ vẫn chạy đúng thì nhiệt độ ở đó phải là bao nhiêu?
Hướng dẫn:
a/ Tại mặt đất t1= 250c, T = 2s. Lên độ cao h nhiệt độ môi trường không thay đổi nên chu kỳ tăng lên. Đồng hồ chạy chậm.
Sau 1 tuần (7.24.3600s) đồng hồ chạy chậm một thời gian:
$\theta =\tau \frac{\left| \Delta T \right|}{{{T}_{1}}}=\tau \frac{h}{R}=7.24.3600.\frac{1,5}{6400}=141,75s$
b/ ở độ cao h =1,5km, nhiệt độ t2 . Muốn chu kỳ con lắc không thay đổi ( vẫn là T) $\Rightarrow \Delta T=0\Rightarrow \frac{\Delta T}{{{T}_{1}}}=0$.
Vận dụng công thức: $\Rightarrow \frac{\Delta T}{{{T}_{1}}}=\frac{1}{2}\alpha \Delta t+\frac{h}{R}\Rightarrow \frac{1}{2}\alpha \Delta t+\frac{h}{R}=0$
$\Rightarrow {{t}_{2}}={{t}_{1}}-\frac{2h}{R\alpha }=25-\frac{2.1,5}{{{6400.2.10}^{-5}}}=1,{{56}^{0}}$
Ví dụ 3:
Một con lắc đơn có chu kỳ dao động nhỏ tại mặt đất T = 2,006s.
a/ Tính chiều dài của con lắc biết tại mặt đất g = 9,8m/s2.
b/Để chu kỳ của con lắc không thay đổi khi đưa lên độ cao h người ta đã thay đổi chiều dài của con lắc 1mm. Hỏi chiều dài đã tăng hay giảm? Độ cao h bằng bao nhiêu?
Hướng dẫn:
a/ Vận dụng công thức:\[T=2\pi \sqrt{\frac{l}{g}}\] . Suy ra l=1m
b/ Khi lên cao gia tốc trọng trường giảm. Để chu kỳ không đổi thì chiều dài cũng phải giảm. Gọi \[\Delta l\] là độ giảm chiều dài thì \[\Delta l={{l}_{2}}-{{l}_{1}}=-1mm\] Vận dụng công thức: $\Rightarrow \frac{\Delta T}{{{T}_{1}}}=\frac{1}{2}\frac{\Delta l}{{{l}_{1}}}+\frac{h}{R}$.
\[\Rightarrow \Delta T=0\Rightarrow h\approx \frac{R}{2}\frac{\Delta l}{l}\] Thay số h=3,2km.
Ví dụ 4:
Một con lắc đơn dao động điều hoà có chu kỳ T= 1 s tại Hà Nội có gia tốc trọng trường là g1= 9,787 m/s2,đưa con lắc sang Pa-ri có gia tốc g2 = 9,805 m/s2,coi nhiệt độ ở 2 nơi là như nhau.
a/ Tại Pa-ri chu kỳ con lắc tăng hay giảm? sai lệch bao nhiêu phần trăm so với tại Hà Nội?
b/ Muốn chu kỳ dao động của con lắc tại Pa-ri vẫn là 1s thì chiều dài con lắc phải thay đổi như thế nào so với chiều dài ban đầu?
Hướng dẫn:
+ Tại Hà Nội: g1= 9,787 m/s2 ; T= 1 s
Tại Pa-ri chu kỳ dao động T’:
a/ Vận dụng công thức: $\frac{\Delta T}{T}\approx -\frac{1}{2}\frac{\Delta g}{{{g}_{1}}}=-\frac{1}{2}\frac{9,805-9,787}{9,787}=-9,{{2.10}^{-4}}$
. Vậy chu kỳ tại Pa-ri giảm.
$\frac{\left| \Delta T \right|}{T}=9,{{2.10}^{-4}}=0,092%$
b/ Để tại Pa-ri chu kỳ con lắc vẫn là 1s thì $\Delta T=0$.
Vận dụng công thức: $\frac{\Delta T}{{{T}_{1}}}\approx \frac{1}{2}\frac{\Delta l}{{{l}_{1}}}-\frac{1}{2}\frac{\Delta g}{{{g}_{1}}}\Rightarrow \frac{\Delta l}{{{l}_{1}}}=\frac{\Delta g}{{{g}_{1}}}=\frac{9,805-9,787}{9,878}=1,{{8.10}^{-3}}$
Vậy chiều dài phải tăng thêm 0,18% chiều dài ban đầu.
Dạng 4: Chu kỳ con lắc đơn thay đổi khi có thêm lực lạ.
* Phương pháp:
Ngoài trọng lực $\overrightarrow{P}$ con lắc còn chịu thêm tác dụng của những lực $\overrightarrow{F}$ không đổi thì coi như con lắc chịu tác dụng của trọng lực hiệu dụng $\overrightarrow{{{P}_{hd}}}$ với $\overrightarrow{{{P}_{hd}}}$=$\overrightarrow{P}$+$\overrightarrow{F}$
$\overrightarrow{{{P}_{hd}}}$ gây ra $\overrightarrow{{{g}_{hd}}}$ (ở VTCB nếu cắt dây vật sẽ rơi với gia tốc $\overrightarrow{{{g}_{hd}}}$ này)
$\overrightarrow{{{g}_{hd}}}$= $\frac{\overrightarrow{{{P}_{hd}}}}{m}$
Chu kỳ mới của con lắc được xác định bởi: $T=2\pi \sqrt{\frac{l}{{{g}_{hd}}}}$
III. 1 SỐ BÀI TẬP TỰ LUYỆN
Bài 1
Tại một nơi trên mặt đất một con lắc đơn dao động điều hoà.Trong khoảng thời gian $\Delta t$, con lắc thực hiện 60 dao động toàn phần; thay đổi chiều dài con lắc một đoạn 44 cm thì cũng trong khoảng thời gian $\Delta t$ ấy, nó thực hiện 50 dao động toàn phần. Xác định chiều dài ban đầu của con lắc ?
Bài 2
Một đồng hồ quả lắc đếm giây có chu kỳ T = 2s. Quả lắc được coi như một con lắc đơn với dây treo và vật nặng làm bằng đồng có hệ số nở dài
$\alpha $ = 17.10-6K-1. Giả sử đồng hồ chạy đúng ở chân không, nhiệt độ 200c.
Tính chu kỳ của con lắc trong chân không ở 300c ? ở 300c đồng hồ chạy nhanh hay chậm? Mỗi ngày chạy sai bao nhiêu?
Bài 3
Con lắc đồng hồ có dây treo làm bằng thanh kim loại mảnh. khi nhiệt độ môi trường tăng thêm 100c thì trong 12 giờ con lắc chạy chậm 30s. Nếu muốn con lắc chạy mỗi ngày chỉ chậm 45s thì nhiệt độ môi trường phải tăng lên bao nhiêu? Coi gia tốc trọng trường không thay đổi.
Bài 4
Con lắc đơn dao động nhỏ được đưa từ Quảng Ngãi vào thành phố Hồ Chí Minh, thì chu kỳ dao động tăng 0,015%. Xác định gia tốc tại Quảng Ngãi biết gia tốc trọng trương tại Hồ Chí Minh là g = 9,787m/s2?
Bài 5
Đưa một con lắc đơn từ mặt đất lên độ cao h=9,6km. Biết bán kính trái đất R=6400km, coi chiều dài của con lắc đơn không phụ thuộc vào nhiệt độ. Muốn chu kỳ của con lắc đơn không thay đổi thì chiều dài của con lắc phải thay đổi thế nào?
Đáp án
Bài 1 :: l = 100 cm.
Bài 2: chạy chậm 2,00017 s; chạy sai 7,34 s.
Bài 3 :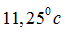
Bài 4: 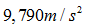
Bài 5: chiều dài con lắc đơn giảm 0,3%chiều dài ban đầu.







