1. Định nghĩa
· Cho D là tập hợp con của R, D khác rỗng. Hàm số f xác định trên D là một qui tắc đặt tương ứng mỗi số x thuộc D với một và chỉ một số y thuộc R.
· x đgl biến số (đối số), y đgl giá trị của hàm số f tại x. Kí hiệu: y = f(x).
· D đgl tập xác định của hàm số.
· T = $\left\{ y=f(x)\left| x\in D \right. \right\}$đgl tập giá trị của hàm số.
2. Cách cho hàm số
· Cho bằng bảng · Cho bằng biểu đồ · Cho bằng công thức y = f(x).
Tập xác định của hàm số y = f(x) là tập hợp tất cả các số thực x sao cho biểu thức f(x) có nghĩa.
3. Đồ thị của hàm số
Đồ thị của hàm số y = f(x) xác định trên tập D là tập hợp tất cả các điểm $M\left( x;f(x) \right)$ trên mặt phẳng toạ độ với mọi x Î D.
Chú ý: Ta thường gặp đồ thị của hàm số y = f(x) là một đường. Khi đó ta nói y = f(x) là phương trình của đường đó.
4. Sư biến thiên của hàm số
Cho hàm số f xác định trên K.
· Hàm số y = f(x) đồng biến (tăng) trên K nếu $\forall {{x}_{1}},{{x}_{2}}\in K:{{x}_{1}}<{{x}_{2}}\Rightarrow f({{x}_{1}})<>
· Hàm số y = f(x) nghịch biến (giảm) trên K nếu $\forall {{x}_{1}},{{x}_{2}}\in K:{{x}_{1}}<{{x}_{2}}\Rightarrow f({{x}_{1}})>f({{x}_{2}})$
5. Tính chẵn lẻ của hàm số
Cho hàm số y = f(x) có tập xác định D.
· Hàm số f đgl hàm số chẵn nếu với mọi x thuộc D thì –x thuộc D và f(–x) = f(x).
· Hàm số f đgl hàm số lẻ nếu với mọi x thuộc D thì –x thuộc D và f(–x) = f(-x).
Chú ý: + Đồ thị của hàm số chẵn nhận trục tung làm trục đối xứng.
+ Đồ thị của hàm số lẻ nhận gốc toạ độ làm tâm đối xứng.
A.Tìm tập xác định của hàm số:
· Tìm tập xác định D của hàm số y = f(x) là tìm tất cả những giá trị của biến số x sao cho biểu thức f(x) có nghĩa: D = $\left\{ x\in R\left| f(x)\,\,co\grave{u}\,\,ngh\acute{o}a \right. \right\}$.
· Điều kiện xác định của một số hàm số thường gặp:
1) Hàm số y = $\frac{P(x)}{Q(x)}$: Điều kiện xác định: Q(x) khác 0.
2) Hàm số y = $\sqrt{R(x)}$: Điều kiện xác định: R(x) lớn hơn bằng 0.
Chú ý: + Đôi khi ta sử dụng phối hợp các điều kiện với nhau.
+ Điều kiện để hàm số xác định trên tập A là A thuộc D.
+ + A.B khác 0.
Ví dụ: Tìm a để hàm số xác định trên tập K đã chỉ ra:
a) $y=\frac{2x+1}{{{x}^{2}}-6x+a-2}$; K = R. ĐS: a > 11
b) $y=\frac{3x+1}{{{x}^{2}}-2ax+4}$; K = R. ĐS: –2 < a < 2
c) $y=\sqrt{x-a}+\sqrt{2x-a-1}$; K = (0; +¥). ĐS: a £ 1
d) $y=\sqrt{2x+a+1}+\frac{1}{x-a}$; K = (1; +¥). ĐS: –1 £ a £ 1
B. Sự biến thiên của hàm số:
Cho hàm số f xác định trên K.
· y = f(x) đồng biến trên K Û $\forall {{x}_{1}},{{x}_{2}}\in K:{{x}_{1}}<{{x}_{2}}\Rightarrow f({{x}_{1}})
Û $\forall {{x}_{1}},{{x}_{2}}\in K:{{x}_{1}}\ne {{x}_{2}}\Rightarrow \frac{f({{x}_{2}})-f({{x}_{1}})}{{{x}_{2}}-{{x}_{1}}}>0$
· y = f(x) nghịch biến trên K Û $\forall {{x}_{1}},{{x}_{2}}\in K:{{x}_{1}}<{{x}_{2}}\Rightarrow f({{x}_{1}})>f({{x}_{2}})$
Û $\forall {{x}_{1}},{{x}_{2}}\in K:{{x}_{1}}\ne {{x}_{2}}\Rightarrow \frac{f({{x}_{2}})-f({{x}_{1}})}{{{x}_{2}}-{{x}_{1}}}<0$
Ví dụ:
- x2+2x
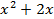 – 2 trên khoảng (–¥; –1), (–1; +¥).
– 2 trên khoảng (–¥; –1), (–1; +¥). - −2x2
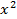 + 4x +1
+ 4x +1 - $y=\frac{4}{x+1}$; (–¥; –1), (–1; +¥).
- $y=\frac{3}{2-x}$; (–¥; 2), (2; +¥)
C. Xét tính chẵn lẻ của hàm số:
Để xét tính chẵn lẻ của hàm số y = f(x) ta tiến hành các bước như sau:
· Tìm tập xác định D của hàm số và xét xem D có là tập đối xứng hay không.
· Nếu D là tập đối xứng thì so sánh f(–x) với f(x) (x bất kì thuộc D).
+ Nếu f(–x) = f(x), "x thuộc D thì f là hàm số chẵn.
+ Nếu f(–x) = –f(x), "x thuộc D thì f là hàm số lẻ.
Chú ý: + Tập đối xứng là tập thoả mãn điều kiện: Với mọi x thuộc D thì –x thuộc D.
Ví dụ:
- 7x2
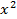 – 1
– 1 - –x4+3x+2
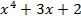
- x+3- 3-x
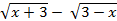
- $y=\frac{\left| x+1 \right|+\left| x-1 \right|}{\left| x+1 \right|-\left| x-1 \right|}$
- $y=2{{x}^{2}}-\left| x \right|$
Chúc các bạn học tốt.







