I.Sự thay đổi R trong mạch R-L-C mắc nối tiếp:
.png)
Xét mạch điện xoay chiều có hiệu hiệu thế hai đầu ổn định : $u={{U}_{0}}\cos (\omega t+{{\varphi }_{u}})$
R là một biến trở, các giá trị R0 , L và C không đổi.
Gọi Rtd = R + R0
1.Có hai giá trị R1 ¹ R2 cho cùng một giá trị công suất
- Công suất tiêu thụ trên mạch là : $P={{R}_{td}}{{I}^{2}}={{R}_{td}}\frac{{{U}^{2}}}{R_{td}^{2}+{{({{Z}_{L}}-{{Z}_{C}})}^{2}}}$
- Vì P1 = P2 = P nên ta có thể xem như công suất trong phương trình trên là một số không đổi ứng với hai giá trị R1 và R2 . Khai triển biểu thức trên ta có:
$PR_{td}^{2}-{{R}_{td}}{{U}^{2}}+P{{({{Z}_{L}}-{{Z}_{C}})}^{2}}=0$
- Nếu có 2 giá trị của điện trở cho cùng một giá trị công suất thì phương trình bậc 2 trên có hai nghiệm phân biệt R1 và R2. Theo định lý Viète (Viet):
.png)
- Từ đó ta thấy rằng có 2 giá trị R1 và R2 khác nhau cho cùng giá trị công suất
1.Giá trị của R làm cho công suất cực đại:
a.Giá trị R làm công suất toàn mạch cực đại:
- Ta có:$P={{R}_{td}}{{I}^{2}}={{R}_{td}}\frac{{{U}^{2}}}{R_{td}^{2}+{{({{Z}_{L}}{{Z}_{C}})}^{2}}}=\frac{{{U}^{2}}}{R_{td}^{{}}+\frac{{{({{Z}_{L}}-{{Z}_{C}})}^{2}}}{R_{td}^{{}}}}$
- Đặt $A=R_{td}^{{}}+\frac{{{({{Z}_{L}}{{Z}_{C}})}^{2}}}{R_{td}^{{}}}$, áp dụng bất đẳng thức Cauchy(Côsi) cho A
$A=R_{td}^{{}}+\frac{{{({{Z}_{L}}-{{Z}_{C}})}^{2}}}{R_{td}^{{}}}\ge 2\sqrt{R_{td}^{{}}\frac{{{({{Z}_{L}}-{{Z}_{C}})}^{2}}}{R_{td}^{{}}}}=2\left| {{Z}_{L}}-{{Z}_{C}} \right|=const$
- Ta thấy rằng Pmax khi Amin => “ =” xảy ra. Vậy: \[{{R}_{td}}=\left| {{Z}_{L}}{{Z}_{C}} \right|\]
- Khi đó giá trị cực đại của công suất là:
${{P}_{\max }}=\frac{{{U}^{2}}}{2\left| {{Z}_{L}}-{{Z}_{C}} \right|}=\frac{{{U}^{2}}}{2\sqrt{{{R}_{1td}}.{{R}_{2td}}}}=\frac{{{U}^{2}}}{2\sqrt{({{R}_{1}}+{{R}_{0}})({{R}_{2}}+{{R}_{0}})}}$
Với R1td và R2td là hai giá trị của R cho cùng giá trị công suất
Lưu ý: Khi $\left| {{Z}_{L}}-{{Z}_{C}} \right|<{{R}_{0}}$thì giá trị biến trở R < 0, khi đó giá trị biến trở làm cho công suất toàn mạch cực đại là R = 0.
a.Giá trị R làm cho công suất của R cực đại:
- Công suất của biến trở R là ${{P}_{R}}={{R}_{{}}}{{I}^{2}}=R\frac{{{U}^{2}}}{(R+{{R}_{0}})_{{}}^{2}+{{({{Z}_{L}}{{Z}_{C}})}^{2}}}=\frac{{{U}^{2}}}{\frac{(R+{{R}_{0}})_{{}}^{2}+{{({{Z}_{L}}-{{Z}_{C}})}^{2}}}{R}}$
- Đặt mẩu thức của biểu thức trên là :
\[A=\frac{(R+{{R}_{0}})_{{}}^{2}+{{({{Z}_{L}}-{{Z}_{C}})}^{2}}}{R}=R+\frac{R_{0}^{2}+{{({{Z}_{L}}-{{Z}_{C}})}^{2}}}{R}+2{{R}_{0}}\]
- Áp dụng bất đẳng thức Cauchy cho A ta được:
\[A=R+\frac{R_{0}^{2}+{{({{Z}_{L}}-{{Z}_{C}})}^{2}}}{R}+2{{R}_{0}}\ge 2\sqrt{R\frac{R_{0}^{2}+{{({{Z}_{L}}-{{Z}_{C}})}^{2}}}{R}}+2{{R}_{0}}=2\sqrt{R_{0}^{2}+{{({{Z}_{L}}-{{Z}_{C}})}^{2}}}+2{{R}_{0}}=const\]
- Ta thấy rằng PRmax khi Amin nghĩa là dấu “ =” phải xảy ra, khi đó:
\[R=\sqrt{R_{0}^{2}+{{({{Z}_{L}}-{{Z}_{C}})}^{2}}}\]
- Công suất cực đại của biến trở R là: \[{{P}_{R\max }}=\frac{{{U}^{2}}}{2\sqrt{R_{0}^{2}+{{({{Z}_{L}}-{{Z}_{C}})}^{2}}}+2{{R}_{0}}}\]
c.Giá trị R làm cho công suất cuộn dây cực đại, cường độ dòng điệncực đại, hiệu điện thế cuộn dây cực đại, hiệu điện thế tụ điện cực đại.
Ta có :
.png)
- Vì R0; ZL; ZC và U là các đại lượng không đổi nên muốn đạt giá trị cực đại thì chỉ cần cường độ dòng điện qua mạch cực đại. Từ biểu thức của dòng điện ta thấy rằng Imax khi giá trị của biến trở R = 0.
3.Khảo sát sự biến thiên của công suất vào giá trị của R
- Để thấy rõ hơn sự phụ thuộc của công suất toàn mạch vào giá trị của biến trở R người ta thường dùng phương pháp khảo sát hàm số:
- Ta có công suất toàn mạch theo biến thiên theo biến trở R cho bởi hàm số:
.png)
Đạo hàm P theo biến số Rtd ta có: ${{P}^{'}}(R)={{U}^{2}}\frac{{{({{Z}_{L}}-{{Z}_{C}})}^{2}}-R_{td}^{2}}{{{(R_{td}^{2}+{{({{Z}_{L}}-{{Z}_{C}})}^{2}})}^{2}}}$
Khi \[{{P}^{'}}(R)=0\Rightarrow {{({{Z}_{L}}-{{Z}_{C}})}^{2}}-R_{td}^{2}=0\Rightarrow {{R}_{td}}=\left| {{Z}_{L}}-{{Z}_{C}} \right|\Rightarrow R=\left| {{Z}_{L}}-{{Z}_{C}} \right|-{{R}_{0}}\]
Bảng biến thiên :
.png)
Nhận xét đồ thị :
+Từ đổ thị ta thấy rằng có hai giá trị R1 và R2 cho cùng một giá trị của công suất
+Công suất đạt giá trị cực đại khi \[R=\left| {{Z}_{L}}-{{Z}_{C}} \right|-{{R}_{0}}>0\]
+Trong trường hợp \[R=\left| {{Z}_{L}}-{{Z}_{C}} \right|-{{R}_{0}}<0\] thì đỉnh cực đại nằm ở phần R< 0 do đó ta thấy rằng công suất của mạch sẽ lớn nhất khi R = 0
+Nếu R0 = 0 thì đồ thị xuất phát từ gốc tọa độ và ta luôn có giá trị R làm cho công suất của toàn mạch cực đại là \[R=\left| {{Z}_{L}}-{{Z}_{C}} \right|\]
Kết luận:
+Với phương pháp khảo sát hàm số để thu được các kết quả ở phần 1 và 2 sẽ không hiệu quả bằng phương pháp dùng tính chất của hàm bậc 2 và bất đẳng thức Cauchy.
+Tuy nhiên từ việc khảo sát này ta có thể biết được sự biến thiên của P theo biến trở R nhằm định tính được giá trị của công suất sẽ tăng hay giảm khi thay đổi điện trở
II.Sự thay đổi L trong mạch R-L-C mắc nối tiếp với cuộn dây thuần cảm.
.png)
Xét mạch điện xoay chiều có hiệu hiệu thế hai đầu ổn định : $u={{U}_{0}}\cos (\omega t+{{\varphi }_{u}})$
L là một cuộn dây thuần cảm có giá trị thay đổi R và C không đổi.
1.Có hai giá trị L1 ¹ L2 cho cùng giá trị công suất
+Vì có hai giá trị của cảm kháng cho cùng giá trị công suất nên:
${{P}_{1}}={{P}_{2}}\Leftrightarrow R\frac{{{U}^{2}}}{{{R}^{2}}+{{({{Z}_{{{L}_{1}}}}-{{Z}_{C}})}^{2}}}=R\frac{{{U}^{2}}}{{{R}^{2}}+{{({{Z}_{{{L}_{2}}}}-{{Z}_{C}})}^{2}}}$
+Khai triển biểu thức trên ta thu được :
.png)
+Suy ra : ${{Z}_{C}}=\frac{{{Z}_{{{L}_{1}}}}+{{Z}_{{{L}_{2}}}}}{2}\Leftrightarrow {{L}_{1}}+{{L}_{2}}=\frac{2}{{{\omega }^{2}}C}$
2.Khảo sát sự biến thiên của công suất theo cảm kháng ZL
+Ta có công suất toàn mạch là: $P=R\frac{{{U}^{2}}}{R_{{}}^{2}+{{({{Z}_{L}}{{Z}_{C}})}^{2}}}$, với R, C là các hằng số, nên công suất của mạch là một hàm số theo biến số ZL
+Đạo hàm của P theo biến số ZL ta có:$P'({{Z}_{L}})=2R{{U}^{2}}\frac{{{Z}_{c}}-{{Z}_{L}}}{[{{R}^{2}}+{{({{Z}_{L}}-{{Z}_{C}})}^{2}}\}{{]}^{2}}}\Rightarrow P'({{Z}_{L}})=0$ khi ${{Z}_{L}}={{Z}_{C}}$
+Bảng biến thiên:
.png)
Nhận xét đồ thị:
+Có hai giá trị của cảm kháng cho cùng một giá trị công suất
+Công suất của mạch cực đại khi ${{Z}_{L}}={{Z}_{C}}=\frac{{{Z}_{{{L}_{1}}}}+{{Z}_{{{L}_{2}}}}}{2}$, với ${{Z}_{{{L}_{1}}}};{{Z}_{{{L}_{2}}}}$là hai giá trị cho cùng một giá trị công suất
Kết luận: Từ việc khảo sát sự biến thiên sự thay đổi công suất vào giá trị của ZL sẽ cho phép định tính được sự tăng hay giảm của P theoZL. Từ đó ta có thể tiên đoán được sự thay đổi của công suất theo giá trị của ZL trong một số bài toán.
3.Giá trị ZL để hiệu điện thế ULmax:
Ta có hiệu điện thế trên cuộn dây là :${{U}_{L}}=I{{Z}_{L}}={{Z}_{L}}\frac{U}{\sqrt{{{R}^{2}}+{{({{Z}_{L}}-{{Z}_{C}})}^{2}}}}$, trong đó R; ZC và U là các hằng số không đổi. Ta có thể dùng phương pháp khảo sát hàm số này theo biến số là ZL. Tuy nhiên với cách khảo sát hàm số sẽ rất phức tạp. Với phương pháp dùng giản đồ Vecto bài toán này có thể giải dể hơn và rút ra nhiều kết luận hơn
.png)
Theo giản đồ vectơ và định lý hàm số sin trong tam giác ta có :$\frac{{{U}_{L}}}{\sin (\alpha +\beta )}=\frac{U}{\sin \gamma }$
Vì $\sin \gamma =\cos \beta =\frac{{{U}_{R}}}{{{U}_{RC}}}=\frac{R}{\sqrt{{{R}^{2}}+Z_{C}^{2}}}=const$, suy ra:
${{U}_{L}}=\frac{U}{\sin \gamma }\sin (\alpha +\beta )=\frac{U}{\cos \beta }\sin (\alpha +\beta )$
Do cosb và U là các giá trị không đổi nên hiệu điện thế ULmax khi $\sin (\alpha +\beta )=1\Rightarrow \alpha +\beta =\frac{\pi }{2}$
Theo hệ thức của tam giác vuông ta có:$U_{RC}^{2}={{U}_{C}}{{U}_{L}}$, từ đó suy ra ${{Z}_{L}}{{Z}_{C}}={{R}^{2}}+Z_{C}^{2}$
Tóm lại:
Khi ${{Z}_{L}}=\frac{{{R}^{2}}+Z_{C}^{2}}{{{Z}_{C}}}$ thì ${{U}_{L\max }}=U\frac{\sqrt{{{R}^{2}}+Z_{C}^{2}}}{R}$
Khi ULmax thì hiệu điện thế tức thời ở hai đầu mạch luôn nhanh pha hơn uRC một góc 900
4.Có hai giá trị L1 ¹ L2 cho cùng giá trị UL , giá trị L để ULmax tính theo L1 và L2
Khi có hai giá trị của L cho cùng một giá trị hiệu điện thế:
${{U}_{{{L}_{1}}}}={{U}_{{{L}_{2}}}}\Leftrightarrow {{Z}_{{{L}_{1}}}}{{I}_{1}}={{Z}_{{{L}_{2}}}}{{I}_{2}}\Leftrightarrow \frac{{{Z}_{{{L}_{1}}}}}{\sqrt{{{R}^{2}}+{{({{Z}_{{{L}_{1}}}}-{{Z}_{C}})}^{2}}}}=\frac{{{Z}_{{{L}_{2}}}}}{\sqrt{{{R}^{2}}+{{({{Z}_{{{L}_{2}}}}-{{Z}_{C}})}^{2}}}}$
Bình phương và khai triển biểu thức trên ta thu được:
\[\frac{Z_{{{L}_{1}}}^{2}}{{{R}^{2}}+Z_{C}^{2}+Z_{{{L}_{1}}}^{2}-2{{Z}_{{{L}_{1}}}}{{Z}_{C}}}=\frac{Z_{{{L}_{2}}}^{2}}{{{R}^{2}}+Z_{C}^{2}+Z_{{{L}_{2}}}^{2}-2{{Z}_{{{L}_{2}}}}{{Z}_{C}}}\]
Theo kết quả phần trên khi hiệu điện thế giữa hai đầu cuộn dây cực đại thì ${{Z}_{L}}{{Z}_{C}}={{R}^{2}}+Z_{C}^{2}$ với giá trị ZL là giá trị làm cho ULmax . Thay vào biểu thức trên:
\[\frac{Z_{{{L}_{1}}}^{2}}{{{Z}_{L}}{{Z}_{C}}+Z_{{{L}_{1}}}^{2}-2{{Z}_{{{L}_{1}}}}{{Z}_{C}}}=\frac{Z_{{{L}_{2}}}^{2}}{{{Z}_{L}}{{Z}_{C}}+Z_{{{L}_{2}}}^{2}-2{{Z}_{{{L}_{2}}}}{{Z}_{C}}}\]
Tiếp tục khai triển biểu thức trên ta thu được:
$(Z_{{{L}_{1}}}^{2}-Z_{{{L}_{2}}}^{2}){{Z}_{L}}=2{{Z}_{{{L}_{1}}}}{{Z}_{{{L}_{2}}}}({{Z}_{{{L}_{1}}}}-{{Z}_{{{L}_{2}}}})$
Vì L1 ¹ L2 nên đơn giàn biểu thức trên ta thu được: ${{Z}_{L}}=\frac{2{{Z}_{{{L}_{1}}}}{{Z}_{{{L}_{2}}}}}{{{Z}_{{{L}_{1}}}}+{{Z}_{{{L}_{2}}}}}\Leftrightarrow L=\frac{2{{L}_{1}}{{L}_{2}}}{{{L}_{1}}+{{L}_{2}}}$ với giá L là giá trị là cho ULmax
5.Giá trị ZL để hiệu điện thế ULRrmax
Khi R và L mắc nối tiếp nhau thì :
${{U}_{LR}}=I\sqrt{{{R}^{2}}+Z_{L}^{2}}=\frac{U\sqrt{{{R}^{2}}+Z_{L}^{2}}}{\sqrt{{{R}^{2}}+{{({{Z}_{L}}-{{Z}_{C}})}^{2}}}}=\frac{U}{\sqrt{\frac{{{R}^{2}}+{{({{Z}_{L}}-{{Z}_{C}})}^{2}}}{{{R}^{2}}+Z_{L}^{2}}}}$
Đặt $MT=\frac{{{R}^{2}}+{{({{Z}_{L}}-{{Z}_{C}})}^{2}}}{{{R}^{2}}+Z_{L}^{2}}$, ta thực hiện việc khảo sát hàm số MT theo biến số ZL để tìm giá trị của ZL sao cho MTmin khi đó giá trị của ULrmax . Đạo hàm của MT theo biến số ZL ta thu được
\[M{{T}^{'}}({{Z}_{L}})=\frac{2({{Z}_{L}}-{{Z}_{C}})({{R}^{2}}+Z_{L}^{2})-2{{Z}_{L}}[{{R}^{2}}+{{({{Z}_{L}}-{{Z}_{C}})}^{2}}]}{{{({{R}^{2}}+Z_{L}^{2})}^{2}}}\]
Cho MT’(ZL) = 0 ta có : \[{{Z}_{C}}Z_{L}^{2}-Z_{C}^{2}{{Z}_{L}}-{{Z}_{C}}{{R}^{2}}=0\]. Nghiệm của phương trình bậc hai này là:
.png)
.png)
Từ bảng biến thiên ta thấy rằng MT đạt giá trị nhỏ nhất nên ULR đạt giá trị lớn nhất. Ta thu được kết quả sau:
III.Sự thay đổi C trong mạch R-L-C mắc nối tiếp
.png)
Xét mạch điện xoay chiều có hiệu hiệu thế hai đầu ổn định : $u={{U}_{0}}\cos (\omega t+{{\varphi }_{u}})$
R là điện trở L là một cuộn dây thuần cảm không đổi và C có giá trị thay đổi .
Nhận xét: Vì trong công thức tổng trở \[Z={{R}^{2}}+{{({{Z}_{L}}-{{Z}_{C}})}^{2}}={{R}^{2}}+{{({{Z}_{C}}-{{Z}_{L}})}^{2}}\] do đó ta thấy rằng bài toán thay đổi giá trị C cũng giống như bài toán thay đổi giá trị L. Do đó khi thực hiện việc khảo sát ta cũng thực hiện tương tự thu được các kết quả sau:
1.Có hai giá trị C1 ¹ C2 cho cùng giá trị công suất
Với hai giá trị C1 và C2 cho cùng giá trị công suất ta có:
.png)
Với giá trị C0 là giá trị làm cho công suất mạch cực đại
2.Khảo sát sự biến thiên của công suất theo dung kháng
Bảng biến thiên:
.png)
3.Giá trị ZC để hiệu điện thế UCmax
- Khi ${{Z}_{C}}=\frac{{{R}^{2}}+Z_{L}^{2}}{{{Z}_{L}}}$ thì
-
-
- \[{{U}_{CM\text{ax}}}=\frac{U\sqrt{{{R}^{2}}+Z_{L}^{2}}}{R}\] và \[U_{CM\text{ax}}^{2}={{U}^{2}}+U_{R}^{2}+U_{L}^{2};\text{ }U_{CM\text{ax}}^{2}-{{U}_{L}}{{U}_{CM\text{ax}}}-{{U}^{2}}=0\]
- uRL vuông pha với hiệu điện thế hai đầu mạch
-
-
4.Có hai giá trị C1 ¹ C2 cho cùng giá trị UC ,giá trị ZC để UCmax tính theo C1 và C2
- Khi có hai giá trị C = C1 hoặc C = C2 cho cùng giá trị UC thì giá trị của C làm cho UCmax khi $\frac{1}{{{Z}_{C}}}=\frac{1}{2}(\frac{1}{{{Z}_{{{C}_{1}}}}}+\frac{1}{{{Z}_{{{C}_{2}}}}})\Rightarrow C=\frac{{{C}_{1}}+{{C}_{2}}}{2}$
1.Giá trị ZC để hiệu điện thế URCmax
- Khi ${{Z}_{C}}=\frac{{{Z}_{L}}+\sqrt{4{{R}^{2}}+Z_{L}^{2}}}{2}$ thì ${{U}_{RCM\text{ax}}}=\frac{2U\text{R}}{\sqrt{4{{R}^{2}}+Z_{L}^{2}}-{{Z}_{L}}}$ ( Với điện trở R và tụ điện mắc gần nhau)
IV.Sự thay đổi w trong mạch R-L-C mắc nối tiếp
1.Giá trị w làm cho Pmax
Ta có \[P=R{{I}^{2}}=R\frac{{{U}^{2}}}{{{R}^{2}}+{{\left( \omega L-\frac{1}{\omega C} \right)}^{2}}}\] , từ công thức này ta thấy rằng công suất của mạch đạt giá trị cực đại khi: $\omega L-\frac{1}{\omega }=0\Rightarrow \omega ={{\omega }_{0}}=\frac{1}{\sqrt{LC}}$. Với ${{P}_{\max }}=\frac{{{U}^{2}}}{R}$
Khi đó Zmin = R và hiệu điện thế giửa hai đầu mạch và cường độ dòng điện qua mạch đồng pha nhau
2.Có hai giá trị w1 ¹ w2 cho cùng công suất và giá trị w làm cho Pmax tính theo w1 và w2
- Nếu có hai giá trị tần số khác nhau cho một giá trị công suất thì:
\[{{\text{P}}_{\text{1}}}=\text{ }{{\text{P}}_{\text{2}}}\text{ }\Leftrightarrow R\frac{{{U}^{2}}}{{{R}^{2}}+{{({{\omega }_{1}}L-\frac{1}{{{\omega }_{1}}C})}^{2}}}=R\frac{{{U}^{2}}}{{{R}^{2}}+{{({{\omega }_{2}}L-\frac{1}{{{\omega }_{2}}C})}^{2}}}\]
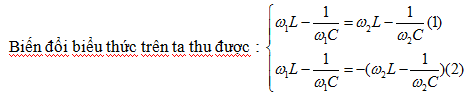
- Vì w1 ¹ w2 nên nghiệm (1) bị loại
- Khai triển nghiệm (2) ta thu được :\[{{\omega }_{1}}{{\omega }_{2}}=\frac{1}{LC}\]
Theo kết quả ta có : \[\omega _{0}^{2}={{\omega }_{1}}{{\omega }_{2}}=\frac{1}{LC}\]với w0 là giá trị cộng hưởng điện
1.Khảo sát sự biến thiên công suất theo w.
- Ta có \[P=R{{I}^{2}}=R\frac{{{U}^{2}}}{{{R}^{2}}+{{\left( \omega L\frac{1}{\omega C} \right)}^{2}}}\]
- Việc khảo sát hàm số P theo biến số w bằng việc lấy đạo hàm và lập bảng biến thiên rất khó khăn vì hàm số này tương đối phức tạp. Tuy nhiên, ta có thể thu được kết quả đó từ những nhận xét sau
- Khi w = 0 thì \[{{Z}_{C}}=\frac{1}{\omega C}\to \infty \] làm cho P = 0
-
-
-
- Khi $\omega ={{\omega }_{0}}=\frac{1}{\sqrt{LC}}$ thì mạch cộng hưởng làm cho công suất trên mạch cực đại
- Khi $\omega \to \infty $ thì ${{Z}_{L}}=\omega L\to \infty $làm cho P = 0
-
-
- Từ những nhận xét đó ta dễ dàng thu được sự biến thiên và đồ thị
.png)
- Nhận xét đồ thị:
- Từ đồ thị ta thấy rằng sẽ có hai giá trị w1 ≠ w2 cho cùng một giá trị công suất, điều này phù hợp với những biến đổi ở phần trên
- 4.Giá trị w làm cho hiệu điện thế ULmax
- Ta có : \[{{U}_{L}}=I.{{Z}_{L}}=\frac{U}{Z}.{{Z}_{L}}=\frac{U}{\frac{Z}{{{Z}_{L}}}}\], đặt $A={{\left( \frac{Z}{{{Z}_{L}}} \right)}^{2}}=\frac{{{R}^{2}}+{{\left( \omega L\frac{1}{\omega C} \right)}^{2}}}{{{(\omega L)}^{2}}}$
- Biến đổi biểu thức A ta thu được : $A=\frac{{{R}^{2}}}{{{\omega }^{2}}{{L}^{2}}}+{{\left( 1\frac{1}{{{\omega }^{2}}LC} \right)}^{2}}$
- Ta tiếp tục đặt $x=\frac{1}{{{\omega }^{2}}L}>0$ khi đó $A=\frac{{{R}^{2}}}{L}x+{{\left( 1\frac{x}{C} \right)}^{2}}$
- Lấy đạo hàm của A theo biến số x ta thu được: \[A'(x)=\frac{{{R}^{2}}}{L}\frac{2}{C}\left( 1-\frac{x}{C} \right)\]
- Cho A’(x) = 0 ta thu được $x=\frac{2LC{{R}^{2}}{{C}^{2}}}{2L}$
- Vì $x>0\Rightarrow \frac{2L}{C}>{{R}^{2}}$khi đó ta thu bảng biến thiên
.png)
- Thay giá trị x vào biểu thức đã đặt ta thu được hiệu điện thế cực đại của cuộn dây là:$\omega =\frac{1}{C}\frac{1}{\sqrt{\frac{L}{C}-\frac{{{R}^{2}}}{2}}}$và ${{U}_{LM\text{ax}}}=\frac{2U.L}{R\sqrt{4LC-{{R}^{2}}{{C}^{2}}}}$
- Nhận xét : Khi $x\le 0\Rightarrow \frac{2L}{C}\le {{R}^{2}}$ thì Amin khi x = 0 do A làm hàm số bậc 2 có hệ số \[a=\frac{1}{{{C}^{2}}}>0\] nên hàm số có cực tiểu ở phần âm, do đó x = 0 làm cho Amin trong miền xác định của x. Khi đó w rất lớn làm cho ZL rất lớn làm cho I = 0. Do đó không thể tìm giá trị w làm cho ULmax
- Nhận xét : Khi $x\le 0\Rightarrow \frac{2L}{C}\le {{R}^{2}}$ thì Amin khi x = 0 do A làm hàm số bậc 2 có hệ số \[a=\frac{1}{{{C}^{2}}}>0\] nên hàm số có cực tiểu ở phần âm, do đó x = 0 làm cho Amin trong miền xác định của x. Khi đó w rất lớn làm cho ZL rất lớn làm cho I = 0. Do đó không thể tìm giá trị w làm cho ULmax
- 5.Giá trị w làm cho hiệu điện thế Ucmax
- Tương tự như cách làm trên ta cũng thu được kết quả tương tự khi thay đổi giá trị w làm cho UCmax là:
- Khi $\omega =\frac{1}{L}\sqrt{\frac{L}{C}-\frac{{{R}^{2}}}{2}}$ thì ${{U}_{CM\text{ax}}}=\frac{2U.L}{R\sqrt{4LC-{{R}^{2}}{{C}^{2}}}}$ với \[\frac{2L}{C}>{{R}^{2}}\]







