Sóng dừng

1. Khái niệm sóng phản xạ.

* Sóng do nguồn phát ra lan truyền trong môi trường khi gặp vật cản thì bị phản xạ và truyền ngược trở lại theo phương cũ. Sóng truyền ngược lại sau khi gặp vật cản gọi là sóng phản xạ

2. Đặc điểm của sóng phản xạ

* Sóng phản xạ có cùng biên độ, tần số với sóng tới.

* Sóng phản xạ có dấu ngược với sóng tới (ngược pha với sóng tới) ở điểm phản xạ nếu đầu phản xạ cố định.

* Sóng phản xạ cùng dấu với sóng tới (cùng pha với sóng tới) ở điểm phản xạ nếu đầu phản xạ tự do.

3. Khái niệm về sóng dừng.

* Sóng dừng là sóng có các bụng và nút sóng cố định.

* Bụng sóng: là những điểm có biên độ dao động cực đại.

* Nút sóng: là những điểm không dao động.

4. Thiết lập phương trình sóng dừng.

* Đầu Q cố định (nút sóng):Phương trình sóng tới và sóng phản xạ tại Q: ${{u}_{B}}=Ac\text{os2}\pi ft$ và $u{{'}_{B}}=-Ac\text{os2}\pi ft=Ac\text{os(2}\pi ft-\pi )$

Phương trình sóng tới và sóng phản xạ tại M cách Q một khoảng d là:

${{u}_{M}}=Ac\text{os(2}\pi ft+2\pi \frac{d}{\lambda })$ và $u{{'}_{M}}=Ac\text{os(2}\pi ft-2\pi \frac{d}{\lambda }-\pi )$

Phương trình sóng dừng tại M: ${{u}_{M}}={{u}_{M}}+u{{'}_{M}}$

${{u}_{M}}=2Ac\text{os}(2\pi \frac{d}{\lambda }+\frac{\pi }{2})c\text{os}(2\pi ft-\frac{\pi }{2})=2A\text{sin}(2\pi \frac{d}{\lambda })c\text{os}(2\pi ft+\frac{\pi }{2})$

Biên độ dao động của phần tử tại M: ${{A}_{M}}=2A\left| c\text{os}(2\pi \frac{d}{\lambda }+\frac{\pi }{2}) \right|=2A\left| \text{sin}(2\pi \frac{d}{\lambda }) \right|$

* Đầu Q tự do (bụng sóng):

Phương trình sóng tới và sóng phản xạ tại Q: ${{u}_{B}}=u{{'}_{B}}=Ac\text{os2}\pi ft$

Phương trình sóng tới và sóng phản xạ tại M cách Q một khoảng d là

${{u}_{M}}=Ac\text{os(2}\pi ft+2\pi \frac{d}{\lambda })$ và $u{{'}_{M}}=Ac\text{os(2}\pi ft-2\pi \frac{d}{\lambda })$

Phương trình sóng dừng tại M: ${{u}_{M}}={{u}_{M}}+u{{'}_{M}}$; ${{u}_{M}}=2Ac\text{os}(2\pi \frac{d}{\lambda })c\text{os}(2\pi ft)$

Biên độ dao động của phần tử tại M: ${{A}_{M}}=2A\left| \text{cos}(2\pi \frac{d}{\lambda }) \right|$

Lưu ý: * Với x là khoảng cách từ M đến đầu nút sóng thì biên độ: ${{A}_{M}}=2A\left| \text{sin}(2\pi \frac{x}{\lambda }) \right|$

* Với x là khoảng cách từ M đến đầu bụng sóng thì biên độ:${{A}_{M}}=2A\left| \text{cos}(2\pi \frac{x}{\lambda }) \right|$

5.Vị trí nút sóng và bụng sóng

Đầu Q cố định (nút sóng): d_nút= \[\frac{k\lambda }{2}\]; d_bụng=\[(k+\frac{1}{2})\frac{\lambda }{2}\]
Đầu Q tự do (bụng sóng): d_bụng= \[\frac{k\lambda }{2}\]; d_nút=\[(k+\frac{1}{2})\frac{\lambda }{2}\]

(d là khoảng cách từ đầu phản xạ đến điểm đang xét)

6. Điều kiện để có sóng dừng trên sợi dây dài l

* Hai đầu là nút sóng: $l=k\frac{\lambda }{2}\text{ }(k\in {{N}^{*}})$

Số bụng sóng = số bó sóng = k ; Số nút sóng = k + 1

Một đầu là nút sóng còn một đầu là bụng sóng:

$l=(2k+1)\frac{\lambda }{4}\text{ }(k\in N)$

Số bó (bụng) sóng nguyên = k; Số bụng sóng = số nút sóng = k + 1

7. Đặc điểm của sóng dừng:

-Khoảng cách giữa 2 nút hoặc 2 bụng liền kề là .

-Khoảng cách giữa nút và bụng liền kề là .

-Khoảng cách giữa hai nút (bụng, múi) sóng bất kỳ là : k..

-Tốc độ truyền sóng: v = lf =

8.Các chú ý đặc biệt về sóng dừng

+ Vấn đề về biên độ:Từ công thức về biên độ sóng:${{A}_{M}}=2A\left| c\text{os}(2\pi \frac{d}{\lambda }+\frac{\pi }{2}) \right|$, dễ dàng thấy biên độ có tính tuần hoàn theo không gian với chu kì l. Những điểm cách nhau một khoảng bằng d sẽ có độ chênh biên độ là\[\Delta \varphi =2\pi \frac{d}{\lambda }\]

Mỗi một điểm trên dây có sóng dừng chỉ có thể dao động với một biên độ xác định, điểm nút có biên độ bằng 0 nên nó luôn đứng yên, điểm bụng có biên độ lớn nhất bằng 2A, nên bề rộng của bụng là 4A.

Việc nhìn thấy hình ảnh sóng dừng là do sự lưu ảnh của mắt, còn hình ảnh tại một thời điểm vẫn là một hình sin hoặc đoạn thẳng.

+Vấn đề về pha dao động

Các điểm trên dây có sóng dừng chỉ có thể dao động đồng pha hoặc ngược pha

Quan sát hai phương trình sóng: ${{u}_{M}}=2Ac\text{os}(2\pi \frac{d}{\lambda }+\frac{\pi }{2})c\text{os}(2\pi ft-\frac{\pi }{2})$

${{u}_{N}}=2Ac\text{os}(2\pi \frac{d}{\lambda }+\frac{\pi }{2})c\text{os}(2\pi ft-\frac{\pi }{2})$

Nhận thấy dấu hiệu hai điểm dao động đồng pha là tích biên độ của chúng là một số dương, và ngược pha nếu tích biên độ giữa chúng phải là một số âm.

+Hai điểm đối xứng qua bụng thì dao động đồng pha

Hai điểm P và Q đối xứng qua bụng thì có biên độ cùng dấu, nên cùng pha. Hai điểm P và R đối xứng qua nút có biên độ khác dấu nên dao động ngược pha.

Hình trên cũng giải thích những điểm dao động trong cùng một bó sóng dao động cùng pha do chúng có cùng dấu của biên độ. Hai bó sóng cạnh nhau có biên độ trái dấu nên luôn dao động ngược pha nhau.

+ Thời gian giữa hai lần sợi dây duỗi thẳng là T/2

Sợi dây duỗi thẳng khi li độ của điểm bụng bằng 0, tức là khi đại lượng

$c\text{os}(2\pi ft-\frac{\pi }{2})=0$ trong phương trình ${{u}_{M}}=2Ac\text{os}(2\pi \frac{d}{\lambda }+\frac{\pi }{2})c\text{os}(2\pi ft-\frac{\pi }{2})$. Khoảng thời gian giữa hai lần li độ điểm bụng bằng 0 là T/2, thể hiện tính tuần hoàn theo thời gian của sóng dừng.

+Phân biệt tốc độ dao động và tốc độ truyền sóng

Tốc độ dao động: v=u’

Tốc độ truyền sóng: v=l.f

B. CÁC DẠNG BÀI TẬP VỀ SÓNG DỪNG

DẠNG 1: PHA DAO ĐỘNG

Phương pháp:Chú ý các điểm dao động khi có sóng dừng chỉ có thể đồng pha hay ngược pha, các điểm trên cùng một bó sóng luôn dao động cùng pha, và ngược pha với bó bên cạnh.

Ví dụ 1: Trên một sợi dây đàn hồi có sóng dừng. Xét hai điểm M, N trên dây không trùng với vị trí của nút sóng, độ lệch pha giữa M và N không thể nhận giá trị nào sau đây?

A. p B. p/2 C. 2p D. 0

Bài giải: Hai điểm chỉ có thể đồng pha hoặc ngược pha nên không thể nhận đáp án B

Ví dụ 2:Người ta tạo ra sóng dừng trên dây với tần số là f1 thì mọi điểm trên dây (không kể đầu dây gắn với âm thoa được xem là nút) đều dao động cùng pha với nhau. Với tần số f2 thì trên dây có sóng dừngvới ba bụng. Tỉ số f2/f1 bằng

A. 4. B. 3. C. 2. D. 5.

Bài giải:

Lúc đầu dây có sóng dừng ứng với nửa bó sóng: $l=(2k+1)\frac{v}{4{{f}_{1}}}\text{ }(k=0)$(1)

Lúc sau dây có 3 bụng sóng : $l=(2k+1)\frac{v}{4{{f}_{2}}}\text{ }(k=2)$(2)

Từ (1) và (2) dễ dàng suy ra: f₂/f₁=5.

DẠNG 2: SÓNG DỪNG TRÊN DÂY

A.LÍ THUYẾT

* Hai đầu là nút sóng: $l=k\frac{\lambda }{2}\text{ }(k\in {{N}^{*}})$

Số bụng sóng = số bó sóng = k ; Số nút sóng = k + 1

Một đầu là nút sóng còn một đầu là bụng sóng: $l=(2k+1)\frac{\lambda }{4}\text{ }(k\in N)$

Số bó (bụng) sóng nguyên = k; Số bụng sóng = số nút sóng = k + 1

B.VÍ DỤ

Ví dụ 1: Một nam điện có dòng điện xoay chiều tần số 50Hz đi qua. Đặt nam châm điện phía trên một dây thép AB căng ngang với hai đầu cố định, chiều dài sợi dây 60cm. Ta thấy trên dây có sóng dừng với 2 bó sóng. Tính vận tốc sóng truyền trên dây?

A.60m/s B. 60cm/s C.6m/s D. 6cm/s

Giải : Vì nam châm có dòng điện xoay chiều chạy qua lên nó sẽ tác dụng lên dây một lực tuần hoàn làm dây dao động cưỡng bức.Trong một T(s) dòng điện đổi chiều 2 lần nên nó hút dây 2 lần . Vì vậy tần số dao động của dây = 2 lần tần số của dòng điện.

Tần số sóng trên dây là: f’ = 2.f =2.50 =100Hz

Vì trên dây có sóng dừng với 2 bó sóng nên: AB = L =2. \[\frac{\lambda }{2}\to \lambda =L=60cm\]

Ta có: v = \[\lambda .f=60.100=6000cm/s=60m/s\]

Ví dụ 2: Một sợi dây AB đàn hồi căng ngang dài l = 120cm, hai đầu cố định đang có sóng dừng ổn định. Bề rộng của bụng sóng là 4a. Khoảng cách gần nhất giữa hai điểm dao động cùng pha có cùng biên độ bằng a là 20 cm. Số bụng sóng trên AB là

A.4 B.6 C.8 D.10

Trước hết hiểu độ rộng của bụng sóng bằng hai lần độ lớn của biên độ bụng sóng :=> KH = 4a

Ap dụng công thức biên độ của sóng dừng tại điểm M với OM = x là khoảng cách tọa độ của M đến một nút gọi là O

A_M = 2a | sin \[\frac{2\pi x}{\lambda }\]| với đề cho A_M = a => | sin \[\frac{2\pi x}{\lambda }\]| = \[\frac{1}{2}\](*)

Đề cho hai điểm gần nhất dao động cùng pha nên , hai điểm M₁ và M₂ phải cùng một bó sóng => OM₁ = x₁ và OM₂ = x₂ ; Dx = x₂ – x₁

Từ (*) suy ra : x₁ = \[\frac{\lambda }{12}\] và x₂ = \[\frac{5\lambda }{12}\]=> \[\Delta x=\frac{5\lambda }{12}-\frac{\lambda }{12}=\frac{\lambda }{3}=20=>\lambda =60cm\]

Chiều dài dây L = \[\frac{n\lambda }{2}=>n=\frac{2L}{\lambda }=\frac{2.120}{60}=4\]

Ví dụ 3: Sóng dừng trên dây AB với chiều dài 0,16 m , đầu B cố định, đầu A dao động với tần số 50 Hz. Biết tốc độ truyền sóng trên dây là 4 m/s.

a. Tính số bụng sóng và số nút sóng.

b. Biểu thức xác định vị trí các nút sóng và bụng sóng

* Hướng dẫn giải:

a. Bước sóng: $\text{ }\!\!\lambda\!\!\text{ = }\frac{\text{v}}{\text{f}}\text{ = }\frac{\text{4}}{\text{50}}\text{ = 0,08(m) = 8(cm)}$

Hai đầu A, B cố định nên có điều kiện:$\ell \text{ = }\frac{\text{k}\lambda }{2}\text{ }\Rightarrow \text{ k = }\frac{2\ell }{\lambda }\text{ = }\frac{2.16}{8}\text{ = 4}$.

Vậy trên dây có 4 bụng sóng và 5 nút sóng

b. Chọn B làm gốc tọa độ, do khoảng cách giữa hai nút sóng liên tiếp là $\frac{\lambda }{2}$nên vị trí các nút sóng xác định từ biểu thức${{\text{d}}_{\text{m}}}\text{= 4k; k = 1;2;3;4; 5}$

Giữa hai nút và bụng liền nhau hơn nhau $\frac{\lambda }{4}$ nên vị trí các bụng sóng xác định từ biểu thức: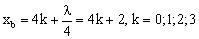

DẠNG 3: SÓNG DỪNG TRONG CỘT KHÔNG KHÍ

Ví dụ 1: Một ống khí có một đầu bịt kín, một đàu hở tạo ra âm cơ bản có tần số 112Hz. Biết tốc độ truyền âm trong không khí là 336m/s. Bước sóng dài nhất của các họa âm mà ống này tạo ra bằng:

A. 1m. B. 0,8 m. C. 0,2 m. D. 2m.

Giải: Điều kiện để có sóng dừng trong ống: \[l=\left( 2k+1 \right)\frac{\lambda }{4}\ \Rightarrow \ \lambda =\frac{4l}{2k+1}\] (*)

(l là chiều dài của cột khí trong ống, đầu kín là nút đầu hở là bụng của sóng dừng trong ống khí)

\[\Rightarrow \ f=\frac{v}{\lambda }=\left( 2k+1 \right)\frac{v}{4l}=\left( 2k+1 \right){{f}_{0}}\] (\[{{f}_{0}}=\frac{v}{4l}\]: tần số âm cơ bản)

Ta có: \[{{f}_{0}}=112Hz\Rightarrow \frac{v}{4l}=112\ \Rightarrow \ l=\frac{v}{4.112}=0,75m\]Âm cơ bản ứng với \[k=0\].

Từ (*) ta thấy các hoạ âm có \[{{\lambda }_{\max }}\] khi \[{{\left( 2k+1 \right)}_{\min }}=3\] (với \[k=1\]) .Vậy: \[\ {{\lambda }_{\max }}=\frac{4l}{3}=1\ \left( m \right)\]. Chọn A

DẠNG 4: BIỂU THỨC SÓNG DỪNG,VẬN TỐC SÓNG DỪNG

Ví dụ 1:Một sợi dây đàn hồi căng ngang, đang có sóng dừng ổn định. Trên dây, A là một điểm nút, B là điểm bụng gần A nhất với AB = 18 cm, M là một điểm trên dây cách B một khoảng 12 cm. Biết rằng trong một chu kỳ sóng, khoảng thời gian mà độ lớn vận tốc dao động của phần tử B nhỏ hơn vận tốc cực đại của phần tử M là 0,1s. Tốc độ truyền sóng trên dây là:
A. 3,2 m/s. B. 5,6 m/s. C. 4,8 m/s. D. 2,4 m/s.

Giải 1: + A là nút; B là điểm bụng gần A nhất \[\Rightarrow \]Khoảng cách AB = \[\frac{\lambda }{4}\]= 18cm

\[\Rightarrow \]\[\lambda \]= 4.18 = 72cm \[\Rightarrow \] M cách B \[\frac{\lambda }{6}\]

+ Trong 1T (2\[\pi \]) ứng với bước sóng \[\lambda \]

Góc quét \[\alpha \] = \[\frac{\lambda }{6}\] \[\Rightarrow \alpha \]=\[\frac{\pi }{3}\]

Biên độ sóng tại B và M: A_B= 2a; A_M = 2acos\[\frac{\pi }{3}\]= a

Vận tốc cực đại của M: v_Mmax= aw

+ Trong 1T vận tốc của B nhỏ hơn vận tốc cực đại của M được biểu diễn trên đường tròn\[\Rightarrow \]Góc quét \[\frac{2\pi }{3}\]

\[\Rightarrow \]\[\frac{2\pi }{3}=\frac{2\pi }{T}.0,1\Rightarrow T=0,3(s)\Rightarrow v=\frac{\lambda }{T}=\frac{72}{0,3}=240cm/s=2,4m/s\]

Ví dụ 2. M,N,P là 3 điểm liên tiếp trên một sợi dây mang sóng dừng có cung biên độ 4mm,dao động tại N ngược pha với dao động tại M. MN=NP/2 = 1cm.Cứ sau những khoảng thời gian ngắn nhất 0,04s thì sợi day có dạng một đoạn thẳng.Tốc độ dao động của phần tử vật chất tại điểm bụng khi qua vị trí cân bằng ( lấy π=3,14)

A.375mm/s B.363mm/s C.314mm/s D.628mm/s

* Tìm $\omega $: Khoảng thời gian giữa 2 lần liên tiếp dây duỗi thẳng là khoảng thời gian giữa 2 lần liên tiếp qua VTCB = T/2 = 0,04s à T=0,08s à $\omega =25\pi $=78,5 (rad/s)

* Tìm ra 3 điểm M,N,P thỏa mãn qua các lập luận sau :

- Các điểm trên dây có cùng biên độ là 4mm có vị trí biên là giao điểm của trục ∆ với dây

- Mà M, N ngược pha nhau à M,N ở 2 phía của nút

- Vì M,N,P là 3 điểm liên tiếp nên ta có M,N,P như hình vẽ

* Qua hình tìm ra bước sóng :

Chiều dài 1 bó sóng là OO'=$\frac{\lambda }{2}$ mà OO'= NP+OP+O'N =NP+2.OP= 3cm à$\lambda =6\,cm$

* Tìm A: ${{A}_{P}}=2A|\sin (2\pi \frac{d}{\lambda })|$ thay số $4mm=2A|\sin (2\pi \frac{5mm}{60mm})|$

à $4mm=2A\frac{1}{2}$ à A=4mm Vậy: ${{v}_{m\text{ax}}}={{\omega }_{bung}.{{A}_{bung}}=\omega .2A$ = 78,5. 2. 4 = 628 mm

DẠNG 5: CÁC ĐIỂM DAO ĐỘNG KHÁC BỤNG,NÚT

Ví dụ 1: Trong thí nghiệm về sóng dừng trên dây có hai đầu cố định, người ta đếm được có n bó

sóng, các vị trí trên dây dao động thì biên độ lớn nhất là A . Số điểm trên dây dao động với biên độ0,5 A là

A. n B. n+1 C. n-1 D. 2n

Bài giải: Mỗi bó sóng có một điểm dao động biên độ A và 2 điểm dao động biên độ 0,5 A nên chọn đáp án D.

Ví dụ 2: Trong thí nghiệm về sóng dừng trên một sợi dây đàn hồi có hai đầu cố định, biên độ dao động của bụng là 4cm. Biên độ dao động của điểm cách bụng một phần tám lần của bước sóng là?

Bài giải: Độ lệch pha giữa điểm M và bụng là: Dj=2p/l=p/4.Biên độ tại M là: Acosp/4=\[2\sqrt{2}\] (cm)

Ví dụ 3: Trên một sợi dây đàn hồi AB dài 25cm đang có sóng dừng, người ta thấy có 6 điểm nút kể cả hai đầu A và B. Hỏi có bao nhiêu điểm trên dây dao động cùng biên độ, cùng pha với điểm M cách A 1cm?

A. 10 điểm B. 9 C. 6 điểm D. 5 điểm

Giải: Dễ thấy trên dây có 5 bó sóng mà độ dài một bó sóng bằng 1/2 bước sóng =5 cm

Trong mỗi bó sóng luôn có 2 điểm cùng biên độ, 2 điểm này đối xứng nhau qua điểm bụng. Do đó trên dây có 10 điểm cùng biên độ với M (kể cả M).

Mặt khác: 2 điểm đối xứng nhau qua nút thì dao động ngược pha, 2 điểm đối xứng nhau qua điểm bụng dao động cùng pha. Từ đó suy ra được số điểm dao động cùng biên độ, cùng pha với M (kể cả M) là 6. Nếu trừ điểm M đi thì trên dây còn 5 điểm thoả mãn

Ví dụ 4: Một dây đàn hồi AB đầu A được rung nhờ một dụng cụ để tạo thành sóng dừng trên dây, biết Phương trình dao động tại đầu A là u_A= acos100pt. Quan sát sóng dừng trên sợi dây ta thấy trên dây có những điểm không phải là điểm bụng dao động với biên độ b (b\[\ne \]0) cách đều nhau và cách nhau khoảng 1m. Giá trị của b và tốc truyền sóng trên sợi dây lần lượt là:

A. a\[\sqrt{2}\]; v = 200m/s. B. a\[\sqrt{3}\]; v =150m/s.

C. a; v = 300m/s. D. a\[\sqrt{2}\]; v =100m/s

Giải: Từ hình vẽ => \[\lambda =\,4\,MN\,=\,4m\]

và MO = 0,5 m = \[\frac{\lambda }{8}\] => b = a\[\sqrt{2}\] và v = 200m/s

DẠNG 6: BÀI TOÁN TẤN SỐ BIẾN THIÊN

Ví dụ 1: Một sợi dây căng giữa hai điểm cố định cách nhau 75cm. Người ta tạo sóng dừng trên dây. Hai tần số gần nhau nhất cùng tạo ra sóng dừng trên dây là 150Hz và 200Hz. Tần số nhỏ nhất tạo ra sóng dừng trên dây đó là

A. 100Hz B. 125Hz C. 75Hz D. 50Hz

Giải: Chọn D. HD: $l=\frac{K\lambda }{2}=\frac{Kv}{2f}\Rightarrow f=\frac{Kv}{2l}\Rightarrow {{f}_{\min }}=\frac{v}{2l}=\frac{\left( K+1 \right)v}{2l}-\frac{Kv}{2l}={{f}_{2}}-{{f}_{1}}=50\left( Hz \right)$

Ví dụ 2:. Một dây đàn hồi dài có đầu A dao động theo phương vuông góc với sợi dây. Tốc độ truyền sóng trên dây là 4m/s. Xét một điểm M trên dây và cách A một đoạn 40cm, người ta thấy M luôn luôn dao động lệch pha so với A một góc Dj = (k + 0,5)p với k là số nguyên. Tính tần số, biết tần số f có giá trị trong khoảng từ 8 Hz đến 13 Hz.

A. 8,5Hz B. 10Hz C. 12Hz D. 12,5Hz

Giải 1:

+ Độ lệch pha giữa M và A là: \[\Delta \phi =\frac{2\pi d}{\lambda }=\frac{2\pi df}{v}\Rightarrow \frac{2\pi df}{v}=(k+0,5)\pi \Rightarrow f=\left( k+0,5 \right)\frac{v}{2d}=5\left( k+0,5 \right)Hz\]

+ Do : \[8Hz\le f\le 13Hz\Rightarrow 8\le \left( k+0,5 \right).5\le 13\Rightarrow 1,1\le k\le 2,1\Rightarrow k=2\Rightarrow f=12,5Hz\].