I.Lý thuyết:
1. (A+B)2 = A2+2AB+B2
2. (A – B)2= A2 – 2AB+ B2
3. A2 – B2= (A-B)(A+B)
4. (A+B)3= A3+3A2B +3AB2+B3
5. (A – B)3 = A3- 3A2B+ 3AB2- B3
6. A3 + B3= (A+B)(A2- AB +B2)
7. A3- B3= (A- B)(A2+ AB+ B2)
8. (A+B+C)2= A2+ B2+C2+2 AB+ 2AC+ 2BC
* CHÚ Ý;
a/ a+b= -(-a-b) ; b/ (a+b)2= (-a-b)2 ; c/ (a-b)2= (b-a)2 ; d/ (a+b)3= -(-a-b)3 e/ (a-b)3=-(-a+b)3
II. Bài tập vận dụng:
Dạng 1 : Tính giá trị của biểu thức
Bài 1 :tính giá trị của biểu thức : A = x2 – 4x + 4 tại x = -1
Giải.
Ta có : A = x2 – 4x + 4 = A = x2 – 2.x.2 + 22 = (x – 2)2
Tại x = -1 : A = ((-1) – 2)2=(-3)2= 9
Vậy : A(-1) = 9
Dạng 2 : Chứng minh biểu thức A không phụ thuộc vào biến
B = (x – 1)2 + (x + 1)(3 – x)
Giải.
B =(x – 1)2 + (x + 1)(3 – x)
= x2 – 2x + 1 – x2 + 3x + 3 – x
= 4 : hằng số không phụ thuộc vào biến x.
Dạng 3 : Tìm giá trị nhỏ nhất của biểu thức
C = x2 – 2x + 5
Giải.
Ta có : C = x2 – 2x + 5 = (x2 – 2x + 1) + 4 = (x – 1)2 + 4
Mà : (x – 1)2 ≥ 0 với mọi x.
Suy ra : (x – 1)2 + 4 ≥ 4 hay C ≥ 4
Dấu “=” xảy ra khi : x – 1 = 0 hay x = 1
Nên : Cmin = 4 khi x = 1
Dạng 4 : Tìm giá trị lớn nhất của biểu thức
D = 4x – x2
Giải.
Ta có : D = 4x – x2 = 4 – 4 + 4x – x2 = 4 – (4 + x2 – 4x) = 4 – (x – 2)2
Mà : -(x – 2)2 ≤ 0 với mọi x.
Suy ra : 4 – (x – 2)2 ≤ 4 hay D ≤ 4
Dấu “=” xảy ra khi : x – 2 = 0 hay x = 2
Nên : Dmax = 4 khi x = 2.
Dạng 5 :Chứng minh đẳng thức
(a + b)3 – (a – b)3 = 2b(3a2 + b2)
Giải.
VT = (a + b)3 – (a – b)3
= (a3 + 3a2b + 3ab2 + b3) – (a3 – 3a2b + 3ab2 – b3)
= a3 + 3a2b + 3ab2 + b3 – a3 + 3a2b – 3ab2 + b3
= 6a2b + 2b3
= 2b(3a2 + b2) ->đpcm.
Vậy : (a + b)3 – (a – b)3 = 2b(3a2 + b2)
Dạng 6 : Chứng minh bất đẳng thức
Biến đổi bất đẳng thức về dạng biểu thức A ≥ 0 hoặc A ≤ 0. Sau đó dùng các phép biến đổi đưa A về 1 trong 7 hằng đẳng thức.
Dạng 7: Phân tích đa thức thành nhân tử
F = x2 – 4x + 4 – y2
Giải.
Ta có : F = x2 – 4x + 4 – y2
= (x2 – 4x + 4) – y2 [nhóm hạng tử]
= (x – 2)2 – y2 [đẳng thức số 2]
= (x – 2 – y )( x – 2 + y) [đẳng thức số 3]
Vậy : F = (x – 2 – y )( x – 2 + y)
Bài 1: A = x3 – 4x2 + 4x
= x(x2 – 4x + 4)
= x(x2 – 2.2x + 22)
= x(x – 2)2
Bài 2: B = x 2 – 2xy – x + 2y
= (x 2– x) + (2y – 2xy)
= x(x – 1) – 2y(x – 1)
= (x – 1)(x – 2y)
Bài 3: C = x2 – 5x + 6
= x2 – 2x – 3x + 6
= x(x – 2) – 3(x – 2)
= (x – 2)(x – 3)
Dạng 8 : Tìm x. biết :
x2 ( x – 3 ) – 4x + 12 = 0
Giải.
x2 ( x – 3 ) – 4x + 12 = 0
x2 ( x – 3 ) – 4(x – 3 ) = 0
( x – 3 ) (x2 – 4) = 0
( x – 3 ) (x – 2)(x + 2) = 0
( x – 3 ) = 0 hay (x – 2) = 0 hay (x + 2) = 0
x = 3 hay x = 2 hay x = –2
vậy : x = 3; x = 2; x = –2
Dạng 9 : Thực hiện phép tính phân thức
Tính giá trị của phân thức M =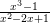 
tại x = –1
Giải.
ta có : M =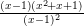 
= 
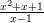
Khi x = -1 : M =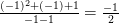 
Vậy : M =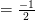 
tại x = -1 .
III. Bài tập tự luyện:
Bài 1: Viết các biểu thức sau dưới dạng bình phương của một tổng hoặc một hiệu.
a) x2 + 2x + 1.
b) 9x2 + y2 + 6xy.
c) 25a2 + 4b2 – 20ab.
d) x2 –x + ¼.
Bài 2: Chứng minh rằng: (10a + 5)2 = 100a (a + 1) + 25.
Bài 3: Viết các đa thức sau dưới dạng bình phương của một tổng hoặc một hiệu:
a) 9x2 +6x + 1.
b) (2x + 3y)2 + 2.( 2x + 3y) + 1.
Bài 4: Chứng minh rằng:
a) ( a+ b)2 = (a-b)2 + 4ab
b) (a-b)2 = (a+b)2 – 4ab
Chúc các bạn học tốt.
