Phép Biến Hình

PHÉP BIẾN HÌNH

A/ LÝ THUYẾT

I/ Phép biến hình

1/ Định nghĩa

Phép biến hình là một quy tắc đặt tương ứng mỗi điểm M của mặt phẳng với một điểm xác định duy nhất M’ của mặt phẳng đó.

2/ Kí hiệu

Phéop biến hình kí hiệu là F. Điểm M có ảnh là M’ qua phép biến hình F, kí hiệu M’ = F(M). Nếu H là một hình qua phép biến hình ta được hình H’, kí hiệu H’ = F(H).

3/ Ví dụ

Cho điểm A và đường thẳng $\vartriangle $ , phép chiếu vuông góc lên đường thẳng $\vartriangle $ của điểm A là một phép biến hình vì với mỗi điểm A ta luôn xác định được duy nhất một điểm A’ là hình chiếu vuông góc của A lên $\vartriangle $.

4/ Phản ví dụ

Cho số dương m tùy ý, trong không gian cho điểm O , với mỗi điểm O trong mặt phẳng, gọi A là điểm sao cho OA = m. Quy tắc đặt điểm A ở trên không phải là một phép biến hình vì với mỗi điểm O trong mặt phẳng thì có vô số điểm A sao cho OA = m (đó là đường tròn tâm O có bán kính R = m).

II/ Phép tịnh tiến

1/ Định nghĩa

+ Trong mặt phẳng, cho vecto $\overrightarrow{v}(a;b)$ . Phép tịnh tiến theo vecto $\overrightarrow{v}(a;b)$ là phép biến hình, biến một điểm M thành điểm M’ sao cho $\overrightarrow{MM'}=\overrightarrow{v}$

+ Kí hiệu: ${{T}_{\overrightarrow{v}}}$

Chú ý: Phép tịnh tiến là một phép biến hình

2/ Các tính chất của phép tịnh tiến

a/ Tính chất 1

Định lí 1: Nếu phép tịnh tiến biến hai điểm M, N lần lượt thành hai điểm M’, N’ thì MN = M’N’.

b/ Tính chất 2

Định lí 2: Phép tịnh tiến biến ba điểm thẳng hàng thành ba điểm thẳng hàng và không làm thay đổi thứ tự của ba điểm đó.

Hệ quả: Phép tịnh tiến biến đường thẳng thành đường thẳng, biến một tia thành một tia, biến một đoạn thẳng thành một đoạn thẳng có độ dài bằng nó, biến một tam giác thành một tam giác bằng nó, biến một đường tròn thành một đường tròn có cùng bán kính, biến một góc thành một góc bằng nó.

3/ Biểu thức tọa độ của phép tịnh tiến

Giả sử cho $\overrightarrow{v}(a;b)$và một điểm $M(x;y)$ . Phép tịnh tiến theo vecto $\overrightarrow{v}(a;b)$ biến điểm M thành điểm M’ thì M’ có tọa độ là:

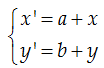
B/ VÍ DỤ

VD 1: Cho vecto $\overrightarrow{v}(-2;1)$ và điểm $M(1;1)$ . Phép tịnh tiến theo vecto $\overrightarrow{v}(-2;1)$ biến điểm M thành điểm M’, tọa độ điểm M’ là:

A.$\left( -1;2 \right)$

B.$\left( 1;2 \right)$

C.$\left( 1;-2 \right)$

D.$\left( -3;0 \right)$

Giải:

Gọi $M'(x;y)$ . Khi đó áp dụng công thức, ta có:

$x=\left( -2 \right)+1=-1$

$y=1+1=2$

Vậy $M'(-1;2)$

Đáp án A

VD 2: Cho vecto $\overrightarrow{v}(2;1)$ và điểm $M(2;2)$ . Phép tịnh tiến theo vecto $\overrightarrow{v}(2;1)$ biến điểm M thành điểm M’, tọa độ trung điểm I của MM’ là:

A. $\left( \frac{5}{2};3 \right)$

B.$\left( 3;\frac{5}{2} \right)$

C.$\left( 6;5 \right)$

D.$\left( 5;6 \right)$

Giải:

Gọi $M'(x;y)$ . Khi đó áp dụng công thức, ta có:

$x=2+2=4$

$y=2+1=3$

$\Rightarrow M'(4;3)$

Khi đó trung điểm $I(a;b)$ của MM’ có tọa độ là:

$a=\frac{{{x}_{M}}+{{x}_{M'}}}{2}=\frac{4+2}{2}=3$

$b=\frac{{{y}_{M}}+{{y}_{M'}}}{2}=\frac{3+2}{2}=\frac{5}{2}$

Vậy $I\left( 3;\frac{5}{2} \right)$

Đáp án B

VD 3: Cho tam giác ABC có tọa độ ba đỉnh là: $A(1;1)$ ; $B(2;2)$ ; $C(3;3)$ . Phép tịnh tiến theo vecto $\overrightarrow{v}(4;4)$ biến tam giác ABC thành tam giác A’B’C’. Tọa độ trọng tâm G’ của tam giác A’B’C’ là:

A.$\left( 10;10 \right)$

B.$\left( 4;4 \right)$

C.$\left( 6;6 \right)$

D.$\left( 2;2 \right)$

Giải:

Phép tịnh tiến theo vecto $\overrightarrow{v}(4;4)$ biến tam giác ABC thành tam giác A’B’C’ thì sẽ biến trọng tâm G của tam giác ABC thành trọng tâm G’ của tam giác A’B’C’

Mà trong tâm của tam giác ABC là $G(2;2)$

Qua phép tịnh tiến theo vecto $\overrightarrow{v}(4;4)$

$\Rightarrow G'(6;6)$

Đáp án C

VD 4: Trong mặt phẳng cho điểm $A(1;2)$ qua phép tịnh tiến theo vecto $\overrightarrow{v}$ biến điểm A thành điểm $A'(4;4)$ . Hỏi cũng theo phép tịnh tiến đó thì biến điểm $B(1;1)$ thành điểm nào sau đây?

A.$\left( 2;3 \right)$

B.$\left( 3;2 \right)$

C.$\left( 3;4 \right)$

D.$\left( 4;3 \right)$

Giải:

Phép tịnh tiến theo vecto $\overrightarrow{v}$ biến điểm A thành A’ suy ra:

$\overrightarrow{v}=\left( 4-1;4-2 \right)=\left( 3;2 \right)$

Phép tịnh tiến theo vecto $\overrightarrow{v}$ biến điểm B thành B’ suy ra tọa độ điểm B’ là:

$B'(3+1;2+1)=B'(4;3)$

Đáp án D

VD 5: Trong mặt phẳng, cho đường tròn $\left( O \right)$ tâm $I(1;1)$ bán kính bằng 3. Phép tịnh tiến theo vecto $\overrightarrow{v}\left( 2;2 \right)$ biến $\left( O \right)$ thành $\left( O' \right)$ . Phương trình của $\left( O' \right)$ là:

A.${{\left( x-3 \right)}^{2}}+{{\left( y-3 \right)}^{2}}=9$

B.${{\left( x-3 \right)}^{2}}+{{\left( y-3 \right)}^{2}}=3$

C.${{\left( x+3 \right)}^{2}}+{{\left( y+3 \right)}^{2}}=9$

D.${{\left( x+3 \right)}^{2}}+{{\left( y+3 \right)}^{2}}=3$

Giải:

Phép tịnh tiến theo vecto $\overrightarrow{v}\left( 2;2 \right)$ biến I thành I’ và R = 3 không đổi

$\Rightarrow I'\left( 3;3 \right)$

$\Rightarrow $ Phương trình đường tròn $\left( O' \right)$ có tâm I’ là:

${{\left( x-3 \right)}^{2}}+{{\left( y-3 \right)}^{2}}=9$

Đáp án A

C/ BÀI TẬP

Bài 1: Cho vecto $\overrightarrow{v}(1;2)$ và điểm $M(1;2)$ . Phép tịnh tiến theo vecto $\overrightarrow{v}(1;2)$ biến điểm M thành điểm M’, tọa độ điểm M’ là:

A.$\left( 0;0 \right)$

B.$\left( 2;4 \right)$

C.$\left( 0;4 \right)$

D.$\left( 2;0 \right)$

Bài 2: Cho vecto $\overrightarrow{v}(-2;0)$ và điểm $M(0;1)$ . Phép tịnh tiến theo vecto $\overrightarrow{v}(1;2)$ biến điểm M thành điểm M’, tọa độ điểm M’ là:

A.$\left( -2;1 \right)$

B.$\left( 2;1 \right)$

C.$\left( -2;-1 \right)$

D.$\left( 2;0 \right)$

Bài 3: Cho vecto $\overrightarrow{v}(-2;0)$ và điểm $M(0;1)$ . Phép tịnh tiến theo vecto $\overrightarrow{v}(-2;0)$ biến điểm M thành điểm M’, tọa độ trung điểm I của MM’ là:

A.$\left( -2;1 \right)$

B.$\left( -4;1 \right)$

C.$\left( -2;\frac{1}{2} \right)$

D.$\left( -4;\frac{1}{2} \right)$

Bài 4: Cho tam giác ABC có tọa độ ba đỉnh là: $A(0;0)$ ; $B(1;1)$ ; $C(2;2)$ . Phép tịnh tiến theo vecto $\overrightarrow{v}(-1;-1)$ biến tam giác ABC thành tam giác A’B’C’. Tọa độ trọng tâm G’ của tam giác A’B’C’ là:

A.$\left( 0;0 \right)$

B.$\left( 1;1 \right)$

C.$\left( -1;-1 \right)$

D.$\left( 2;2 \right)$

Bài 5: Cho đường thẳng $(d):x-2y+3=0$ và vecto $\overrightarrow{v}(-1;2)$ . Tìm phương trình đường thẳng (d’) là ảnh của (d) qua phép tịnh tiến theo vecto $\overrightarrow{v}(-1;2)$

A.$x-2y+7=0$

B.$x-2y+8=0$

C.$x-2y+2=0$

D.$x-2y=0$

Bài 6: Trong mặt phẳng Oxy cho đường thẳng d có phương trình $2x-y+1=0$. Để phép tịnh tiến theo vecto $\overrightarrow{v}$ biến d thành chính nó thì $\overrightarrow{v}$ phải là vecto nào sau đây?

A.$\overrightarrow{v}\left( 2;1 \right)$

B.$\overrightarrow{v}\left( 2;-1 \right)$

C.$\overrightarrow{v}\left( 1;2 \right)$

D.$\overrightarrow{v}\left( -1;2 \right)$

Bài 7: Cho hai đường thẳng d và d’ song song với nhau. Có bao nhiêu phép tịnh tiến biến đường thẳng d thành d’?

A.0

B.2

C.1

D.Vô số

Bài 8: Cho 4 đường thẳng a, b, a’, b’ trong đó a song song với a’, b song song với b’, a cắt b. Có bao nhiêu phép tịnh tiến biến đường thẳng a và b lần lượt thành các đường thẳng a’ và b’?

A.0

B.1

C.2

D.Vô số

Bài 9: Cho đường tròn (O) và hai điểm A, B. Một điểm M thay đổi trên đường tròn (O). Quỹ tích điểm M’ sao cho $\overrightarrow{MM'}+\overrightarrow{MA}=\overrightarrow{MB}$

A.$(O')={{T}_{\overrightarrow{AB}}}\left( \left( O \right) \right)$

B.$(O')={{T}_{\overrightarrow{AM}}}\left( \left( O \right) \right)$

C.$(O')={{T}_{\overrightarrow{BA}}}\left( \left( O \right) \right)$

D.$(O')={{T}_{\overrightarrow{BM}}}\left( \left( O \right) \right)$

Bài 10: Cho lục giác đều ABCDEF tâm O. Tìm ảnh của $\vartriangle AOF$ qua phép tịnh tiến theo vecto $\overrightarrow{AB}$

A.\[\vartriangle ABO\]

B.\[\vartriangle BCO\]

C.\[\vartriangle CDO\]

D.\[\vartriangle DEO\]

ĐÁP ÁN