1. Định nghĩa
Là một nhóm các phần tử có cùng tính chất hoặc có cùng một đặc điểm nào đó. Tập hợp thường được kí hiệu bằng chữ cái in hoa như: $A,B,C,...$
Cho tập hợp $A$,
+ Nếu \(a\) là phần tử thuộc tập $A$ ta viết \(a \in A\)
+ Nếu \(a\) là phần tử không thuộc tập $A$ ta viết \(a \notin A\)
2. Cách xác định tập hợp
Có 2 cách để xác định tập hợp:
a) Liệt kê: Viết tất cả các phần tử của tập hợp vào giữa dấu \(\left\{ {} \right\}\), các phần tử cách nhau bởi dấu “,”.
b) Nêu tính chất đặc trưng: Chỉ ra tính chất đặc trưng của các phần tử.
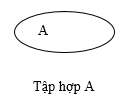
Ta thường minh họa tập hợp bằng một đường cong khép kín gọi là biểu đồ Ven.
3. Tập hợp rỗng
Là tập hợp không chứa phần tử nào, kí hiệu là \(\emptyset \).
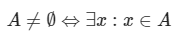
4. Tập con của một tập hợp
Tập hợp $A$ là con của tập hợp $B$ hay còn gọi tập $B$ là tập cha của tập $A$. Kí hiệu: \(A \subset B\).
\(A \subset B \Leftrightarrow \left( {\forall x \in A \Rightarrow x \in B} \right)\)
+) 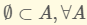
+) ${\rm{A}} \subset {\rm{A,}}\forall {\rm{A}}$
+) $A \subset B,B \subset C \Rightarrow A \subset C$ (bắc cầu).
+ Số tập con của một tập hợp: Tập hợp $A$ gồm có $n$ phần tử thì số tập con của tập hợp $A$ là \(P\left( A \right) = {2^n}\).
+ Số phần tử của một tập hợp \(A\) là \(n(A)\) hoặc \(\left| A \right|\)
5. Hai tập hợp bằng nhau
\(A = B \Leftrightarrow \forall x,\left( {x \in A \Leftrightarrow x \in B} \right) \Leftrightarrow \left\{ \begin{array}{l}A \subset B\\B \subset A\end{array} \right.\)







