I.Lý thuyết:
1.Tổng của 2 vecto:
Định nghĩa: Cho hai vecto 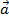 ,
, 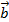 , lấy một điểm A tùy ý, vẽ
, lấy một điểm A tùy ý, vẽ 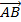 =
= 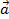 ,
, 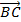 =
= 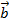 . Vecto AC được gọi là tổng của hai vecto
. Vecto AC được gọi là tổng của hai vecto 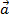 ,
, 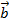 . Ta kí hiệu tổng của hai vecto
. Ta kí hiệu tổng của hai vecto 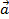 ,
, 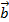 là
là 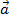 +
+ 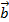 . Vậy AC =
. Vậy AC = 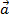 +
+ 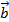 .
.
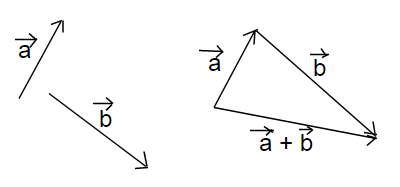
Phép toán tìm tổng của hai vecto gọi là phép cộng vecto.
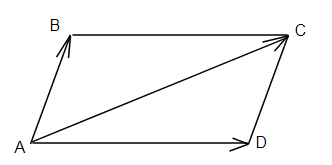
a. Quy tắc hình bình hành:
Minh họa phép cộng hai vecto bằng quy tắc hình bình hành như sau:
Nếu ABCD là hình bình hành thì:: 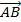 +
+ 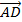 =
= 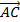 .
.
b. Tính chất phép cộng vecto:
Với 3 vecto 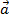 ,
, 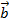 ,
, 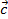 tùy ý, ta có:
tùy ý, ta có:
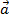 +
+ 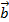 =
= 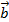 +
+ 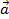 (Tính chất giao hoán).
(Tính chất giao hoán).
(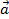 +
+ 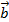 ) +
) + 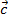 =
= 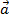 + (
+ (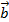 +
+ 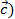
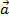 + 0 = 0 +
+ 0 = 0 + 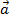 =
= 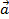 (Tính chất của vecto – không)
(Tính chất của vecto – không)
2. Hiệu của hai vecto:
Vecto có cùng độ dài và ngược hướng với 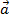 được gọi là vecto đối của
được gọi là vecto đối của 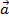 . Kí hiệu là -
. Kí hiệu là -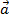 .
.
Mỗi vecto đều có vecto đối, chẳng hạn vecto đối của 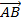 =
= 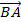 . Có nghĩa là -
. Có nghĩa là -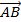 =
= 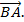
Vecto đối của 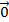 là vecto
là vecto 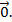
Định nghĩa: Cho hai vecto a, b, ta gọi hiệu của a trừ b 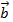 bằng tổng của vecto
bằng tổng của vecto 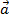 với vecto đối của vecto
với vecto đối của vecto 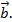
Như vậy 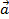 -
- 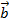 =
= 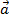 + ( -
+ ( -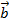 ).
).
Minh họa:
.png)
3. Quy tắc tam giác:
Với 3 điểm A, B, C bất kì, theo quy tắc cộng trừ vecto, ta có:
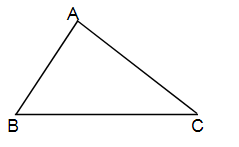
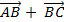 =
= 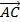 (Qui tắc 3 điểm)
(Qui tắc 3 điểm)
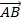 -
- 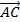 =
= 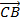 (Qui tắc trừ hai vecto có chung điểm đầu)
(Qui tắc trừ hai vecto có chung điểm đầu)
4. Áp dụng:
a.Nếu I là trung điểm AB thì 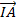 +
+ 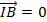
b. Nếu G là trọng tâm tam giác ABC thì 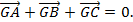
.png)
Lấy D là điểm đối xứng với G qua E, khi đó BGCD là hình bình hành (hai đường chéo cắt nhau tại trung điểm mỗi đường) và G là trung điểm của AD (vì GA = 2GE = GD).
Ta có: 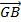 +
+ 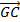 =
= 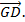
Suy ra: 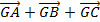 =
= 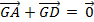
II. Bài tập vận dụng:
.png)
Giải:
Trên đoạn thẳng AB ta lấy điểm M′ để có →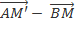

Như vậy 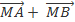 =
= 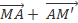 = '
= '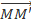
Vậy vecto '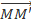 chính là vecto tổng của
chính là vecto tổng của 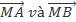
'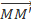 =
= 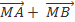
Ta lại có: 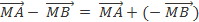
-
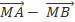 =
= 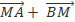
Theo tính chất giao hoán của tổng vecto ta có:
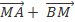 =
= 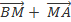 =
= 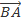 (quy tắc 3 điểm)
(quy tắc 3 điểm)
Vậy 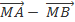 =
= 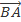
.png)
Giải:
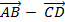 =
= 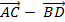
.png)
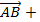
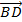 =
= 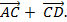
.png)
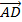 =
= 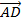 .
.
.png)
Giải:
Trong tam giác đều ABC, tâm O của đường tròn ngoại tiếp cũng là trọng tâm tam giác. Vậy 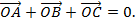
.png)
Giải:
Ta có: 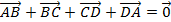
.png)
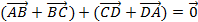
.png)
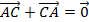
.png)
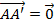
.png)
Giải:
Ta có: 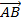 -
- 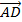 =
= 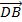 ,
, 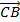 -
- 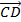 =
= 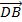 .
.
Từ đó suy ra: 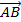 -
- 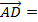
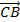 -
- 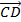
III. Bài tập tự luyện:
Bài 1: Cho tam giác ABC có trung tuyến AM. Trên cạnh AC lấy hai điểm E và F sao cho AE = EF = FC; BE cắt AM tại N. Chứng minh 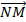 và
và 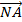 là hai vecto đối nhau.
là hai vecto đối nhau.
Bài 2: Cho hình bình hành ABCD. Gọi O là một điểm bất kì trên đường chéo AC. Qua O kẻ các đường thẳng song song với các cạnh của hình bình hành. Các đường thẳng này cắt AB và DC lần lượt tại M và N, cắt AD và BC lần lượt tại E và F. Chứng minh rằng 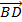 =
= 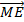 +
+ 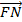 .
.
Bài 3: Cho tứ giác ABCD, Chứng minh rằng tứ giác ABCD là hình bình hành khi và chỉ khi 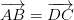 .
.
Bài 4: Cho hình lục giác đều ABCDEF có tâm O. Tìm Véctơ khác và cùng phương .
Bài 5: Cho tam giác đều ABC cạnh a. tính độ dài các vectơ :
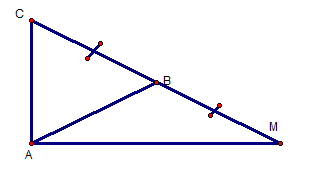
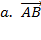 +
+ 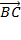 .
.
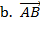 -
- 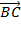 .
.
Bài 6: Hình vuông ABCD cạnh a. Tính độ dài các vectơ :
a. 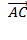 +
+ 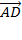 .
.
b. 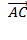 -
- 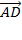 .
.
Bài 7: Cho tam giác ABC, bên ngoài tam giác vẽ các hình bình hành ABIJ, BCPQ, CARS. Chứng minh rằng: 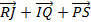 =
= 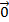 .
.
Bài 8: Cho hình bình hành tâm O. Chứng minh rằng
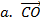 -
- 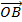 =
= 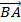 .
.
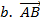 -
- 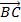 =
= 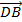 .
.
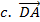 -
- 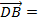
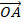 -
- 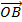 .
.
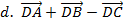 = 0.
= 0.
Chúc các bạn học tốt.







