Hàm Số Bậc Nhất và Hàm Số Bậc Hai

I.HÀM SỐ BẬC NHẤT:

 1. Định nghĩa:  Hàm số bậc nhất là hàm số có công thức: y = ax + b trong đó a và b là các số đã cho với a ≠ 0, x là biến số.

2. Sự biến thiên:

    Hàm số bậc nhất y = ax + b (a≠0) có tập xác định D=R, đồng biến trên R nếu a>0 và nghịch biến trên R nếu a<0.

    Bảng biến thiên của hàm số bậc nhất tùy theo a như sau:

3. Đồ thị

Đồ thị hàm số y=ax+b(a≠0) là một đường thẳng không song song cũng không trùng với các trục tọa độ, cắt trục tung tại điểm P(0;b) và cắt trục hoành tại điểm Q=(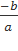;0)

4. Hàm số hằng y=b

Khi a=0 hàm số y=ax+b trở thành hàm hằng y=b là đường thẳng song song với trục hoành cắt trục tung tại điểm P(0;b). Ta gọi đường thẳng này là đường thẳng y=b. 

5. Ví dụ:

 

VD1: Vẽ đồ thị hàm số y = -3x + 3

 

Giải:

Cho x=0 thì y=3, ta được điểm P(0; 3) thuộc trục tung Oy

Cho y=0 thì x=1, ta được điểm Q(1; 0) thuộc trục hoành Ox

VD2: a. Cho đồ thị hàm số y=ax+7 đi qua M(2; 11). Tìm a.

b. Biết rằng khi x=3 thì hàm số y=2x+b có giá trị bằng 8, tìm b.

c. Cho hàm số y=(m+1)x. Xác định m để đồ thị hàm số đi qua A(1; 2).

 

Giải:

a, Vì đồ thị hàm số y=ax+7 (1) đi qua M(2; 11) nên thay x=2; y=11 vào (1) ta được:11=2a+7. Từ đó suy ra a=2.

Vậy a=2.

b, Thay y=8; x=3 vào hàm số y=2x+b ta được: 8=6+b. Suy ra b=2

Vậy b=2.

c, Vì đồ thị hàm số y=(m+1)x (2) đi qua A(1; 2) nên thay x=1; y=2 vào (2) ta được: 2=(m+1).1. Từ đó suy ra m=1

Vậy m=1.

II.HÀM SỐ BẬC HAI:

1.Định nghĩa: Hàm số bậc hai là hàm số có công thức: y=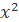+bx+c(a≠0) có miền xác định D=R.

2. Bảng biến thiên: 

 

3. Ví dụ:

a)  Xác định tọa độ của đỉnh và các giao điểm với trục tung, trục hoành (nếu có) của mỗi parabol.

y=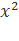−3x+2

Hệ số: a=1,b=−3,c=2.

Hoành độ đỉnh =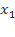 

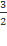
Tung độ đỉnh  =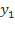 

 

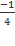
          Vậy đỉnh parabol là I()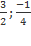

• Giao điểm của parabol với trục tung là A(0;2).
• Hoành độ giao điểm của parabol với trục hoành là nghiệm của phương trình:

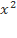 −3x+2=0

⇔x=1; x=2

b) Lập bảng biến thiên và vẽ đồ thị của các hàm số.

a) y=3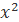−4x+1

Đồ thị:

- Đỉnh: I(;)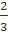

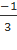- Trục đối xứng: x=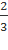

- Giao điểm với trục tung A(0;1)

- Giao điểm với trục hoành B(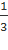;0)

III. BÀI TẬP TỰ LUYỆN:

1. Vẽ đồ thị của các hàm số sau:

       a) $y=2x-7$                      b) $y=-3x+5$              c) $y=\frac{x-3}{2}$             d) $y=\frac{5-x}{3}$

2. Tìm toạ độ giao điểm của các cặp đường thẳng sau:

       a) $y=3x-2;y=2x+3$                     b) $y=-3x+2;y=4(x-3)$

            c) $y=2x;y=-x-3$                    d)  $y=\frac{x-3}{2};y=\frac{5-x}{3}$

3. Xác định a và b để đồ thị của hàm số $y=ax+b$:

       a) Đi qua hai điểm A(–1; –20), B(3; 8).   

       b) Đi qua điểm M(4; –3) và song song với đường thẳng d: $y=-\frac{2}{3}x+1$.

       c) Cắt đường thẳng d₁: \[~y=2x+5\] tại điểm có hoành độ bằng –2 và cắt đường thẳng d₂: \[y=3x+4\] tại điểm có tung độ bằng –2.

       d) Song song với đường thẳng $y=\frac{1}{2}x$ và đi qua giao điểm của hai đường thẳng $y=-\frac{1}{2}x+1$ và \[y=3x+5\].

4. Xét sự biến thiên của các hàm số sau:

       a) $y=-{{x}^{2}}+4x-1$ trên (-¥; 2)     b) \[y=\frac{x+1}{x-1}\] trên (1; +¥) c) \[y=\frac{1}{\sqrt{x-1}}\]

       d) \[y=\sqrt{3-2x}\]                                  e) \[y=\frac{1}{\sqrt{x}-2}\]                          f) $y=\frac{x+3}{x-2}$ trên (2; +∞)

5. Xét tính chẵn lẻ của các hàm số sau:

       a) \[y=\frac{{{x}^{4}}+{{x}^{2}}-2}{{{x}^{2}}-1}\]                                   b) \[y=\sqrt{3+x}+\sqrt{3-x}\]      c) \[y=x({{x}^{2}}\text{+ }2\left| x \right|)\]

       d) \[y=\frac{\left| x+1 \right|+\left| x-1 \right|}{\left| x+1 \right|-\left| x-1 \right|}\]                        e) \[y=\frac{{{\left| x \right|}^{3}}x}{{{x}^{2}}+1}\]                          f) \[y=\sqrt{x-2}\]

Chúc các bạn học tốt.

 

Bài viết gợi ý: