Tính điện trở tương đương mạch nối tiếp, mạch song song và mạch cầu

TÍNH ĐIỆN TRỞ TƯƠNG ĐƯƠNG MẠCH NỐI TIẾP, MẠCH SONG SONG, MẠCH CẦU

A)Phương pháp giải:$$

-Mạch điện mắc nối tiếp các điện trở: $R={{R}_{1}}+{{R}_{2}}+...+{{R}_{n}}$

Các điện trở mắc nối tiếp

-Mạch điện mắc song song các điện trở: $\frac{1}{R}=\frac{1}{{{R}_{1}}}+\frac{1}{{{R}_{2}}}+...+\frac{1}{{{R}_{n}}}$

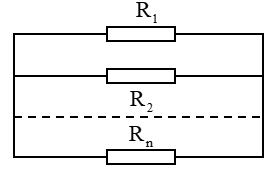
Các điện trở mắc song song

+Nếu có 2 điện trở:

$\frac{1}{R}=\frac{1}{{{R}_{1}}}+\frac{1}{{{R}_{2}}}\Rightarrow R=\frac{{{R}_{1}}{{R}_{2}}}{{{R}_{1}}+{{R}_{2}}}$

+Nếu có n-R$_{0}$ giống nhau:

$\frac{1}{R}=\frac{1}{{{R}_{0}}}+...+\frac{1}{{{R}_{0}}}\Rightarrow R=\frac{{{R}_{0}}}{n}$

-Mạch điện trở phức tạp có đoạn nối tắt (dây nối không điện trở) thì:

+Đồng nhất các điểm cùng điện thế (chập mạch).

+Vẽ lại sơ đồ lí thuyết và thực hiện tính toán theo sơ đồ.

-Trong trường hợp đoạn mạch có cấu tạo đối xứng, có thể lí luận dựa vào sự đối xứng để định các điểm đồng nhất về điện thế.

-Trường hợp đặc biệt:

Mạch cầu cân bằng: ${{I}_{5}}=0\Rightarrow \frac{{{R}_{1}}}{{{R}_{3}}}=\frac{{{R}_{2}}}{{{R}_{4}}}$

Ta bỏ R hoặc chập 2 điểm M và N lại và vẽ lại mạch như một trong 2 hình sau:

Mạch cầu không cân bằng: $\frac{{{R}_{1}}}{{{R}_{3}}}\ne \frac{{{R}_{2}}}{{{R}_{4}}}$

Từ chuyển từ mạch tam giác sang mạch hình sao hoặc ngược lại.

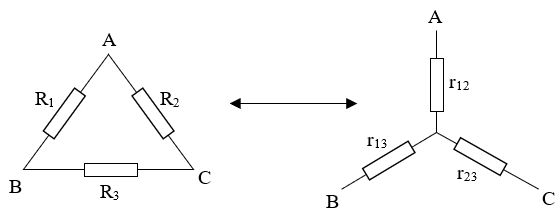
Với: ${{r}_{12}}=\frac{{{R}_{1}}{{R}_{2}}}{{{R}_{1}}+{{R}_{2}}+{{R}_{3}}}$; ${{r}_{13}}=\frac{{{R}_{1}}{{R}_{3}}}{{{R}_{1}}+{{R}_{2}}+{{R}_{3}}}$;

${{r}_{23}}=\frac{{{R}_{2}}{{R}_{3}}}{{{R}_{1}}+{{R}_{2}}+{{R}_{3}}}$

B)Ví dụ minh họa:

Ví dụ 1: Hai dây dẫn, khi mắc nối tiếp có điện trở gấp 6,25 lần khi mắc song song. Tính tỉ số điện trở của hai dây?

A.1/4 B.2 C.4 D.1/2

Hướng dẫn:

Ta có: ${{R}_{1}}+{{R}_{2}}=6,25.\frac{{{R}_{1}}{{R}_{2}}}{{{R}_{1}}+{{R}_{2}}}$

$\Leftrightarrow {{\left( {{R}_{1}}+{{R}_{2}} \right)}^{2}}-6,25{{R}_{1}}{{R}_{2}}=0$

$\Leftrightarrow R_{1}^{2}-4,25{{R}_{1}}{{R}_{2}}+R_{2}^{2}=0$

$\Leftrightarrow {{\left( {{R}_{1}}-2,125{{R}_{2}} \right)}^{2}}={{(1,875{{R}_{2}})}^{2}}$

$\Leftrightarrow {{R}_{1}}-2,125{{R}_{2}}=1,875{{R}_{2}}$

$\Rightarrow {{R}_{1}}=4{{R}_{2}}$ (loại giá trị âm) $\Rightarrow \frac{{{R}_{1}}}{{{R}_{2}}}=4$

Chọn đáp án C.

Ví dụ 2: Cho mạch điện như hình vẽ. Biết ${{R}_{1}}={{R}_{3}}=2\Omega $, ${{R}_{2}}={{R}_{5}}=4\Omega $, ${{R}_{4}}=4\Omega $. Tính điện trở tương đương của mạch.

A.5$\Omega $ B.2$\Omega $ C.6$\Omega $ D.3$\Omega $

Hướng dẫn:

Ta có: $\frac{{{R}_{1}}}{{{R}_{2}}}=\frac{{{R}_{3}}}{{{R}_{4}}}=0,5\Rightarrow $Mạch cầu cân bằng nên dòng điện qua R$_{5}$ bằng 0 nên bỏ đoạn R$_{5}$ đi ta có mạch (R$_{1}$ nt R$_{2}$)//(R$_{3}$ nt R$_{4}$).

Ta có: ${{R}_{12}}={{R}_{1}}+{{R}_{2}}$=6; ${{R}_{34}}={{R}_{3}}+{{R}_{4}}$=6

Vậy điện trở tương đương của mạch:

$R=\frac{{{R}_{12}}{{R}_{34}}}{{{R}_{12}}+{{R}_{34}}}=\frac{6.6}{6+6}=3\Omega $

Chọn đáp án D.

Ví dụ 3: Tính điện trở tương đương của đoạn mạch hình dưới, biết rằng các điện trở đều bằng nhau và bằng R=12$\Omega $.

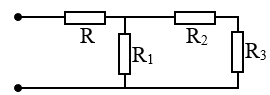
A.20$\Omega $ B.12$\Omega $ C.8$\Omega $ D.24$\Omega $

Hướng dẫn:

Vì R$_{2}$ và R$_{3}$ mắc nối tiếp nên ta có: ${{R}_{23}}={{R}_{2}}+{{R}_{3}}=24\Omega $

+Vì R$_{1}$ mắc song song với R$_{23}$ nên:

$\frac{1}{{{R}_{1-23}}}=\frac{1}{{{R}_{1}}}+\frac{1}{{{R}_{23}}}\Rightarrow {{R}_{1-23}}=\frac{{{R}_{1}}{{R}_{23}}}{{{R}_{1}}+{{R}_{23}}}=8\Omega $

+Vì R mắc nối tiếp với R$_{1-23}$ nên: ${{R}_{t\text{d}}}=R+{{R}_{1-23}}=12+8=20\Omega $

Chọn đáp án A.

Ví dụ 4: Tính điện trở tương đương của mạch điện biết:${{R}_{1}}=1\Omega ,{{R}_{2}}=2,4\Omega ,{{R}_{3}}=2\Omega ,{{R}_{4}}=5\Omega ,{{R}_{5}}=3\Omega $

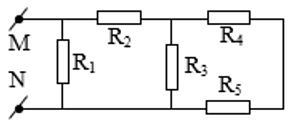
A.0,8$\Omega $ B.1,2$\Omega $ C.0,6$\Omega $ D.1,5$\Omega $

Hướng dẫn:

+Vì R$_{4}$ và R$_{5}$ mắc nối tiếp nên ta có: ${{R}_{45}}={{R}_{4}}+{{R}_{5}}=8\Omega $

+Vì R$_{3}$ mắc song song với R$_{45}$ nên:

$\frac{1}{{{R}_{3-45}}}=\frac{1}{{{R}_{3}}}+\frac{1}{{{R}_{45}}}\Rightarrow {{R}_{3-45}}=\frac{{{R}_{3}}{{R}_{45}}}{{{R}_{3}}+{{R}_{45}}}=1,6\Omega $

+Vì R$_{2}$ mắc nối tiếp với R$_{3-45}$ nên : ${{R}_{2-3-45}}={{R}_{2}}+{{R}_{3-45}}=4\Omega $

+Do R$_{1}$ mắc song song với R$_{2-3-45}$ nên:

$\frac{1}{{{R}_{td}}}=\frac{1}{{{R}_{1}}}+\frac{1}{{{R}_{2-3-45}}}\Rightarrow {{R}_{td}}=\frac{{{R}_{1}}{{R}_{2-3-45}}}{{{R}_{1}}+{{R}_{2-3-45}}}=0,8\Omega $

Chọn đáp án A.

Ví dụ 5: Cho đoạn mạch điện như hình vẽ. Trong đó ${{R}_{1}}=15\Omega ,{{R}_{2}}=10\Omega ,{{R}_{3}}=10\Omega ,{{R}_{4}}=10\Omega $. Tính điện trở tương đương của đoạn mạch đó.

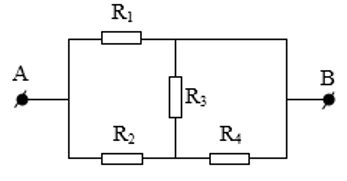
A.5$\Omega $ B.7,5$\Omega $ C.6,5$\Omega $ D.6$\Omega $

Hướng dẫn:

+Gọi M là điểm nối giữa điện trở R$_{2}$, R$_{3}$ và R$_{4}$.

Mạch điện được vẽ lại như sau:

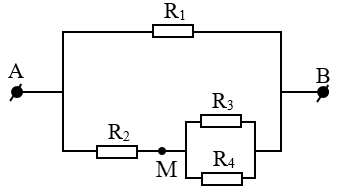
+Vì (R$_{3}$ // R$_{4}$) nên:

$\frac{1}{{{R}_{34}}}=\frac{1}{{{R}_{3}}}+\frac{1}{{{R}_{4}}}=\frac{1}{10}+\frac{1}{10}\Rightarrow {{R}_{34}}=5\Omega $

+Vì (R$_{1}$ // R$_{234}$) nên:

$\frac{1}{{{R}_{AB}}}=\frac{1}{{{R}_{1}}}+\frac{1}{{{R}_{234}}}=\frac{1}{15}+\frac{1}{15}\Rightarrow {{R}_{AB}}=7,5\Omega $

Chọn đáp án B.

Ví dụ 6: Dây dẫn có điện trở R=144$\Omega $. Phải cắt dây ra bao nhiêu đoạn bằng nhau để khi mắc các đoạn đó song song nhau, điện trở tương đương là 4$\Omega $ ?

A.3 B.5 C.6 D.7

Hướng dẫn:

Điện trở của mỗi đoạn dây sau khi cắt là:

${{R}_{0}}=\frac{R}{n}$

Điện trở tương của n đoạn dây giống nhau mắc //:

${{R}_{td}}=\frac{{{R}_{0}}}{n}=\frac{R}{{{n}^{2}}}\Rightarrow n=\sqrt{\frac{R}{{{R}_{td}}}}=\sqrt{\frac{144}{4}}=6$.

Chọn đáp án C.

Ví dụ 7:Cho mạch điện như hình vẽ. Biết ${{R}_{1}}={{R}_{3}}=2\Omega ,{{R}_{2}}={{R}_{5}}=4\Omega ,{{R}_{4}}=5\Omega $. Tính điện trở tương đương của mạch.

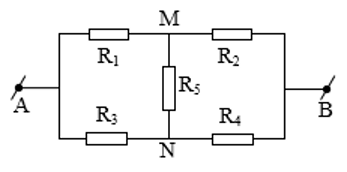
A.3,2$\Omega $ B.2,4$\Omega $ C.4,6$\Omega $ D.5,2$\Omega $

Hướng dẫn:

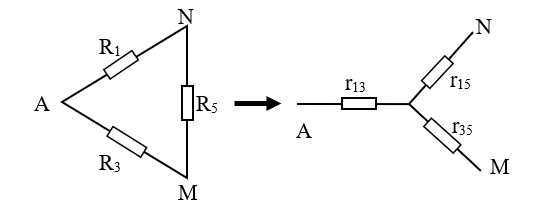
+Ta có: $\frac{{{R}_{1}}}{{{R}_{2}}}\#\frac{{{R}_{3}}}{{{R}_{4}}}\Rightarrow $ Mạch cầu không cân bằng.

+Trước tiên ta chuyển mạch có dạng tam giác AMN thành mạch hình sao.

Với: ${{r}_{13}}=\frac{{{R}_{1}}{{R}_{3}}}{{{R}_{1}}+{{R}_{3}}+{{R}_{5}}}=0,5\Omega $ ; ${{r}_{15}}=\frac{{{R}_{1}}{{R}_{5}}}{{{R}_{1}}+{{R}_{3}}+{{R}_{5}}}=1\Omega $ ;

${{r}_{35}}=\frac{{{R}_{3}}{{R}_{5}}}{{{R}_{1}}+{{R}_{3}}+{{R}_{5}}}$

+Mạch điện được vẽ lại đầy đủ như hình.

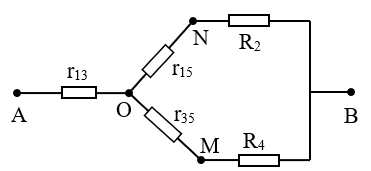
Ta có:

${{R}_{152}}={{r}_{15}}+{{R}_{2}}=1+4=5\Omega $

${{R}_{354}}={{r}_{35}}+{{R}_{4}}=1+5=6\Omega $

+Lại có: ${{R}_{OB}}=\frac{{{R}_{152}}{{R}_{354}}}{{{R}_{152}}+{{R}_{354}}}=\frac{30}{11}\Omega $

+Vậy điện trở tương đương của mạch là:

${{R}_{AB}}={{r}_{13}}+{{R}_{OB}}=\frac{71}{22}\Omega \approx 3,2\Omega $

Chọn đáp án A.

Ví dụ 8: Tính điện trở tương đương của mạch điện biết: ${{R}_{1}}=1\Omega ,{{R}_{2}}={{R}_{3}}=2\Omega ,{{R}_{4}}=0,8\Omega $.

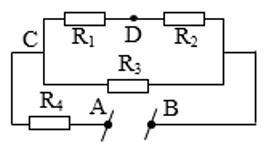
A.2,2$\Omega $ B.0,8$\Omega $ C.0,7$\Omega $ D.2$\Omega $

Hướng dẫn:

+Vì R$_{1}$ mắc nối tiếp với R$_{2}$ nên: ${{R}_{12}}={{R}_{1}}+{{R}_{2}}=3\Omega $

+Vì R$_{12}$ mắc song song với R$_{3}$ nên:

$\frac{1}{{{R}_{12-3}}}=\frac{1}{{{R}_{12}}}+\frac{1}{{{R}_{3}}}\Rightarrow {{R}_{12-3}}=\frac{{{R}_{12}}{{R}_{3}}}{{{R}_{12}}+{{R}_{3}}}=1,2\Omega $

+R$_{4}$ mắc nối tiếp với R$_{12-3}$ nên:

${{R}_{td}}={{R}_{4}}+{{R}_{12-3}}=1,2\Omega $

Chọn đáp án D.

Ví dụ 9: Cho mạch điện như hình vẽ. Biết: ${{R}_{1}}=15\Omega ,{{R}_{2}}={{R}_{3}}={{R}_{4}}=10\Omega ,{{R}_{A}}=0$. Tìm R$_{AB}$ ?

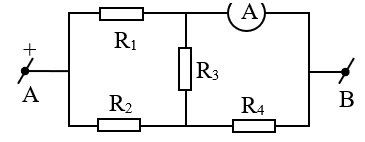
A.7,5$\Omega $ B.8$\Omega $ C.8,5$\Omega $ D.9$\Omega $

Hướng dẫn:

Gọi C là giao điểm của (${{R}_{1}},{{R}_{3}},{{R}_{A}}$), D là giao điểm của (${{R}_{2}},{{R}_{3}},{{R}_{4}}$)

Vì ampe kế có điện trở không đáng kể nên B và C có cùng điện thế $\to $ chập C và B lại.

Mạch điện được vẽ lại như sau:

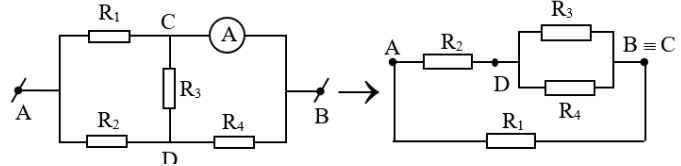
$\frac{1}{{{R}_{12-3}}}=\frac{1}{{{R}_{12}}}+\frac{1}{{{R}_{3}}}\Rightarrow {{R}_{12-3}}=\frac{{{R}_{12}}.{{R}_{3}}}{{{R}_{12}}+{{R}_{3}}}=1,2\Omega $

Ta có: [R$_{2}$ nt (R$_{3}$ // R$_{4}$)] // R$_{1}$

Chọn đáp án A

Ví dụ 10: Cho mạch điện như hình vẽ. Trong đó ${{R}_{1}}=22,5\Omega ,{{R}_{2}}=12\Omega ,{{R}_{3}}=5\Omega ,{{R}_{4}}=15\Omega $. Tính điện trở tương đương của đoạn mạch đó.

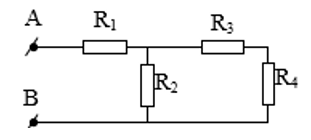
A.25$\Omega $ B.35$\Omega $ C.20$\Omega $ D.30$\Omega $

Hướng dẫn:

+Vì R$_{3}$ và R$_{4}$ mắc nối tiếp nên ta có: ${{R}_{34}}={{R}_{3}}+{{R}_{4}}=20\Omega $

+Vì R$_{2}$ mắc song song với R$_{34}$ nên:

$\frac{1}{5}+\frac{1}{T}=\frac{1}{Z}\Leftrightarrow \frac{1}{T}=\frac{1}{2,5}-\frac{1}{5}\Rightarrow T=5\Omega $

+Vì R$_{1}$ mắc nối tiếp với R$_{234}$ nên: ${{R}_{td}}={{R}_{1}}+{{R}_{234}}=7,5+22,5=30\Omega $.

Chọn đáp án D.

C)Câu hỏi tự luyện:

Câu 1: Cho một đoạn mạch như hình vẽ dưới đây. Biết rằng: ${{R}_{1}}=1\Omega ,{{R}_{2}}=20\Omega ,{{R}_{3}}=5\Omega ,{{R}_{4}}={{R}_{5}}=10\Omega $.Hãy tính điện trở tương đương của đoạn mạch?

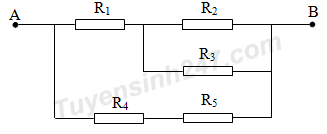
A.4$\Omega $ B.2$\Omega $ C.3$\Omega $ D.5$\Omega $

Câu 2: Tính điện trở tương đương của mạch điện như hình vẽ. Cho ${{R}_{1}}=0,4\Omega ,{{R}_{2}}=8\Omega $. Số ô điện trở là vô hạn. Tìm điện trở tương đương của mạch?

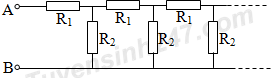
A.4$\Omega $ B.2$\Omega $ C.3$\Omega $ D.5$\Omega $

Câu 3: Đoạn mạch AB gồm 2 điện trở R$_{1}$=12$\Omega $ và

R$_{2}$=36$\Omega $ mắc nối tiếp. Đặt 1 hdt không đổi 24V giữa hai đầu đoạn mạch A,B. Mắc thêm điện trở R$_{3}$ song song với R$_{1}$. Tính điện trở R$_{3}$ để cđdđ qua mạch là 0,6A.

A.12$\Omega $ B.3$\Omega $ C.8$\Omega $ D.6$\Omega $

Câu 4: Cho ba điện trở giống nhau cùng giá trị 8$\Omega $, hai điện trở mắc song song và cụm đó nối tiếp với điện trở còn lại. Đoạn mạch này được nối với nguồn có điện trở trong 2$\Omega $ thì hiệu điện thế ở hai đầu nguồn là 12V. Cường độ dòng điện trong mạch và suất điện động của mạch khi đó là:

A.1A và 14V B.0,5A và 13V C.0,5A và 14V D.1A và 13V

Câu 5: Cho mạch điện như hình vẽ:

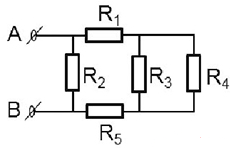
Trong đó: ${{R}_{1}}={{R}_{3}}={{R}_{5}}=3\Omega ,{{R}_{2}}=8\Omega ,{{R}_{4}}=6\Omega ,{{U}_{5}}=6V$. Tính cường độ dòng điện chạy qua điện trở thứ 4?

A.3A B.2/3A C.4/3A D.2A

Câu 6: Cho mạch điện như hình vẽ:

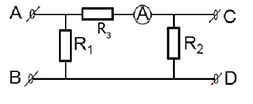
Nếu đặt vào AB hiệu điện thế 100V thì người ta có thể lấy ra ở hai đầu CD một hiệu điện thế U$_{CD}$=40V và ampe kế chỉ 1A. Tính cường độ dòng điện ở đầu A.

A.2A B.3A C.0,5A D.1A

Câu 7: Cho mạch điện như hình vẽ:

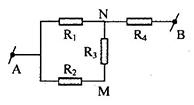
Cho ${{R}_{1}}={{R}_{2}}={{R}_{3}}=6\Omega ,{{R}_{4}}=2\Omega $. Tính điện trở tương đương của mạch khi nối M và B bằng một vôn kế có điện trở rất lớn.

A.6$\Omega $ B.5$\Omega $ C.7$\Omega $ D.8$\Omega $

Câu 8: Cho mạch điện như hình vẽ:

Cho ${{U}_{MN}}=4V,{{R}_{1}}={{R}_{2}}=2\Omega ,{{R}_{3}}={{R}_{4}}={{R}_{5}}=1\Omega ,{{R}_{A}}=0,{{R}_{V}}=\infty $. Tính số chỉ của vôn kế.

A.3V B.4V C.2V D.5V

Câu 9: Cho mạch điện như hình vẽ:

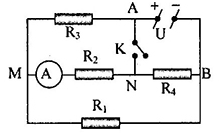
Cho U$_{AB}$= 7,2V không đổi, ${{R}_{1}}={{R}_{2}}={{R}_{3}}=2\Omega ,{{R}_{4}}=6\Omega $. Điện trở của ampe kế và khóa K không đáng kể. Tìm số chỉ của ampe kế khi K đóng.

A.2,4A B.2A C.1,2A D.1A

Câu 10: Cho mạch điện như hình vẽ:

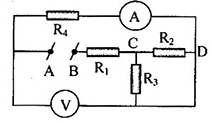
Cho U$_{AB}$ =18V, ${{R}_{1}}={{R}_{2}}={{R}_{3}}={{R}_{4}}=6\Omega $, điện trở ampe kế không đáng kể, điện trở vôn kế vô cùng lớn. Đổi chỗ ampe kế và vôn kế cho nhau. Tính số chỉ của vôn kế lúc này.

A.1V B.2V C.0V D.0,5V