CỰC TRỊ HÀM SỐ

A. LÝ THUYẾT

1. Định nghĩa:

Cho hàm số y = f(x) xác định  trên tập D và x0∈D{{x}_{0}}\in D

- Nếu tồn tại một khoảng (a;b) chứa điểm x0 sao cho (a;b)⊂D(a;b)\subset D và f(x) < f(x0) với mọi x∈(a;b)/ &NegativeThinSpace;&NegativeThinSpace;{&NegativeThinSpace;&NegativeThinSpace; x0 &NegativeThinSpace;&NegativeThinSpace;}&NegativeThinSpace;&NegativeThinSpace; x\in (a;b)/\text{ }\!\!\{\!\!\text{ }{{x}_{0}}\text{ }\!\!\}\!\!\text{ } thì ta nói hàm số f(x) đạt cực đại tại x0 và f(x0) được gọi là giá trị cực đại của hàm số.

- Nếu tồn tại một khoảng (a;b) chứa điểm x0 sao cho (a;b)⊂D(a;b)\subset D và f(x) > f(x0) với mọi x∈(a;b)/ &NegativeThinSpace;&NegativeThinSpace;{&NegativeThinSpace;&NegativeThinSpace; x0 &NegativeThinSpace;&NegativeThinSpace;}&NegativeThinSpace;&NegativeThinSpace; x\in (a;b)/\text{ }\!\!\{\!\!\text{ }{{x}_{0}}\text{ }\!\!\}\!\!\text{ } thì ta nói hàm số f(x) đạt cực tiểu tại x0 và f(x0) được gọi là giá trị cực tiểu của hàm số.

2. Điều kiện cần để có cực trị

Giả sử hàm số f đạt cực trị tại điểm x0. Khi đó, nếu f có đạo hàm tại x0 thì f’(x0) = 0

3. Điều kiện đủ để hàm số có cực trị

Giả sử hàm số y=f(x) liên tục trên K

- Nếu f’(x) đổi dấu từ dương sang âm khi đi qua x0 thì x0 là một điểm cực đại của hàm số f(x).

- Nếu f’(x) đổi dấu từ âm sang dương khi đi qua x0 thì x0 là một điểm cực tiểu của hàm số f(x).

4. Quy tắc tìm cực trị của hàm số

* Quy tắc 1:

Bước 1: TÌm tập xác định của hàm số.

Bước 2: Tính f’(x). Tìm các điểm tại đó f’(x) = 0 hoặc f’(x) không xác định.

Bước 3: Lập bảng biến thiên.

Bước 4: Từ bảng biến thiên suy ra các điểm cực trị.

*Quy tắc 2:

Bước 1: Tìm tập xác định của hàm số

Bước 2: Tính f’(x). Giải phương trình f’(x) và kí hiệu xi­ là các nghiệm của nó.

Bước 3: Tính f’’(x) và f’’(xi).

Bước 4: Dựa vào dấu của f’’(xi) suy ra tính chất cực trị của điểm xi.

5. Kỹ năng giải nhanh các bài toán cực trị hàm bậc ba y=ax3+bx2+cx+d(a≠0)y=a{{x}^{3}}+b{{x}^{2}}+cx+d(a\ne 0)

Ta có y′=3ax2+2bx+cy&#x27;=3a{{x}^{2}}+2bx+c

-Đồ thị hàm số của hai điểm cực trị khi y’=0 có hai nghiệm phân biệt

↔b2−3ac&gt;0\leftrightarrow {{b}^{2}}-3ac&gt;0 . Khi đó đường thẳng qua hai điểm cực trị đó là:

y=(2c3−2b29a)x+d−bc9ay=(\frac{2c}{3}-\frac{2{{b}^{2}}}{9a})x+d-\frac{bc}{9a}

-CASIO tìm ra đường thẳng qua hai điểm cực trị:

   ax3+bx2+cx+d−(3ax2+2bx+c)(x3+b9a)a{{x}^{3}}+b{{x}^{2}}+cx+d-(3a{{x}^{2}}+2bx+c)(\frac{x}{3}+\frac{b}{9a})

 cho x=i →Ai+B→y=Ax+B\to Ai+B\to y=Ax+B

Hoặc sử dụng công thức y−y′.y′′18ay-\frac{y&#x27;.y&#x27;&#x27;}{18a}

-Khoảng cách giữa hai điểm cực trị hàm bậc 3 là:

AB=4e+16e3aAB=\sqrt{\frac{4e+16{{e}^{3}}}{a}} với e=b2−3ac9ae=\frac{{{b}^{2}}-3ac}{9a}

6. Kỹ năng giải nhanh các bài toán cực trị hàm trùng phương

Cho hàm số:

(C) có ba điểm cực trị khi y’=0 có 3 nghiệm phân biệt khi a,b trái dấu

Giả sử A(0;c) là điểm cực trị thuộc trục tung

Khi đó AB=AC=b416a2−b2a,BC=2−b2aAB=AC=\sqrt{\frac{{{b}^{4}}}{16{{a}^{2}}}-\frac{b}{2a}},BC=2\sqrt{-\frac{b}{2a}}

*Các kết quả cần nắm

+ ∆ABC vuông cân ⇔b38a+1=0\Leftrightarrow \frac{{{b}^{3}}}{8a}+1=0

+ ∆ABC đều ⇔b38a+3=0\Leftrightarrow \frac{{{b}^{3}}}{8a}+3=0

+ ∠BAC=α\angle BAC=\alpha , ta có

+ S△ABC=b24∣a∣−b2a{{S}_{\vartriangle ABC}}=\frac{{{b}^{2}}}{4\left| a \right|}\sqrt{-\frac{b}{2a}}

+ Bán kính đường tròn ngoại tiếp ∆ABC  là R=b3−8a8∣a∣bR=\frac{{{b}^{3}}-8a}{8\left| a \right|b}

+ Bán kính đường tròn nội tiếp ∆ABC là r=b24∣a∣+16a2−2ab3r=\frac{{{b}^{2}}}{4\left| a \right|+\sqrt{16{{a}^{2}}-2a{{b}^{3}}}}

+ Phương trình đường tròn ngoại tiếp ∆ABC  là: x2+y2−(2b−△4a+c)y+c(2b−△4a)=0{{x}^{2}}+{{y}^{2}}-\left( \frac{2}{b}-\frac{\vartriangle }{4a}+c \right)y+c\left( \frac{2}{b}-\frac{\vartriangle }{4a} \right)=0

B. VÍ DỤ

VD 1: Cho hàm số y=x2−4x+1x+1.y=\frac{{{x}^{2}}-4x+1}{x+1}. Hàm số có 2 điểm cực trị x1,x2{{x}_{1}},{{x}_{2}} .Tích x1x2{{x}_{1}}{{x}_{2}} bằng

A.1

B.-5

C.-1

D.-4

HD: Ta có y′=(2x−4)(x+1)−x2+4x−1(x+1)2=x2−2x−5(x+1)2y&#x27;=\frac{(2x-4)(x+1)-{{x}^{2}}+4x-1}{{{(x+1)}^{2}}}=\frac{{{x}^{2}}-2x-5}{{{(x+1)}^{2}}}

Khi đó x1,x2{{x}_{1}},{{x}_{2}} là nghiệm của phương trình x2−2x−5=0{{x}^{2}}-2x-5=0 khi đó theo Vi-ét x1.x2=−5→B{{x}_{1}}.{{x}_{2}}=-5\to B

VD 2: Số điểm cực trị của hàm số y=x4−2x2−3y={{x}^{4}}-2{{x}^{2}}-3  là

A.1

B.2

C.3

D.4

HD: Hàm bậc 4 trùng phương y=ax4+bx2+cy=a{{x}^{4}}+b{{x}^{2}}+c có 3 cực trị khi a,b trái dấu

Ta thấy 1.(-2) <0 nên hàm đã cho có 3 cực trị => C

VD 3:  Hàm số có y′=(x+2)2(x−3)3y&#x27;={{(x+2)}^{2}}{{(x-3)}^{3}} có mấy điểm cực trị

A.1

B.2

C.3

D.0

HD: Ta thấy nhưng y’ chỉ đổi dấu khi đi qua điểm x=3 => Hàm số đã cho có 1 điểm cực trị

  • A

VD 4:  Cho hàm số y=x2+2x+1x−3y=\frac{{{x}^{2}}+2x+1}{x-3} . Hàm số có hai điểm cực trị x1,x2{{x}_{1}},{{x}_{2}} .Tổng x1+x2{{x}_{1}}+{{x}_{2}} bằng:

A.-6

B.3

C.6

D.7

HD: Ta có y′=(2x+2)(x−3)−x2−2x−1(x−3)2=x2−6x−7(x−3)2y&#x27;=\frac{(2x+2)(x-3)-{{x}^{2}}-2x-1}{{{(x-3)}^{2}}}=\frac{{{x}^{2}}-6x-7}{{{(x-3)}^{2}}}

Khi đó x1,x2{{x}_{1}},{{x}_{2}} là nghiệm của phương trình x2−6x−7=0{{x}^{2}}-6x-7=0 . Theo Vi-ét x1+x2=6{{x}_{1}}+{{x}_{2}}=6

=>C

VD 5:  Với giá trị nào của tham số m, hàm số y=x3−3x2+mx−1y={{x}^{3}}-3{{x}^{2}}+mx-1 có hai điểm cực trị x1,x2{{x}_{1}},{{x}_{2}} sao cho x12+x22=3x_{1}^{2}+x_{2}^{2}=3

A.m=32m=\frac{3}{2}

B.m=−32m=-\frac{3}{2}

C.m=3

B.m=-3

HD: Ta có y′=3x2−6x+my&#x27;=3{{x}^{2}}-6x+m . Khi đó x1,x2{{x}_{1}},{{x}_{2}} là nghiệm của phương trình

3x2−6x+m=03{{x}^{2}}-6x+m=0 . Theo Vi-ét, ta có:

Ta có: x12+x22=3⇔(x1+x2)2−2x1x2=3⇔4−2m3=2⇔m=3x_{1}^{2}+x_{2}^{2}=3\Leftrightarrow {{({{x}_{1}}+{{x}_{2}})}^{2}}-2{{x}_{1}}{{x}_{2}}=3\Leftrightarrow 4-\frac{2m}{3}=2\Leftrightarrow m=3

=>C

C. BÀI TẬP

Câu 1: Cho hàm số y=f(x)y=f(x) có đồ thị như hình vẽ

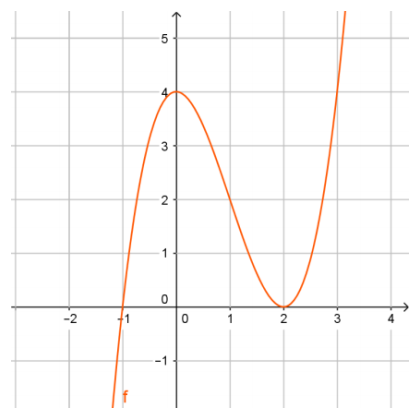
Đồ thị trên có mấy điểm cực trị?

A.2

B.1

C.0

D.3

Câu 2: Cho hàm số y=f(x)y=f(x) có bảng biến thiên:

Khẳng định nào sau đây đúng ?

A.Hàm số đạt cực đại tại x=2

B.Hàm số đạt cực đại tại x=3

C.Hàm số đạt cực đại tại x=4

D.Hàm số đạt cực đại tại x=-2

Câu 3: Biết đồ thị hàm số y=x3−3x+1y={{x}^{3}}-3x+1 có hai điểm cực trị A, B. Khi đó phương trình đường thẳng AB là:

A.y = x - 2

B.y = 2x – 1

C.y = -2x + 1

D.y = -x + 2

Câu 4: Gọi M, n lần lượt là giá trị cực đại, cực tiểu của hàm số y=x2+3x+3x+2y=\frac{{{x}^{2}}+3x+3}{x+2} . Khi đó giá trị của biểu thức M2−2n{{M}^{2}}-2n bằng:

A.8

B.7

C.9

D.6

Câu 5: Cho hàm số y=f(x)=∣x2−2x−4∣y=f(x)=\left| {{x}^{2}}-2x-4 \right| có đồ thị như hình vẽ

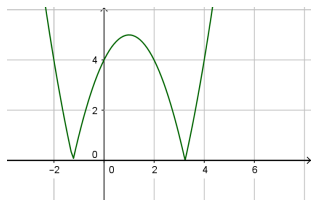
Hàm số y=f(x)y=f(x) có mấy cực trị?

A.4

B.1

C.3

D.2

Câu 6: Cho hàm số y=f(x)y=f\left( x \right) có đạo hàm f′(x)=x(x+1)(x−2)f&#x27;\left( x \right)=x\left( x+1 \right)\left( x-2 \right) . Tìm số điểm cực trị của hàm số y=f(x)y=f\left( x \right)

A.0

B.1

C.2

D.3

Câu 7: Cho hàm số y=f(x)y=f\left( x \right) có đạo hàm f′(x)=x4(x+1)4(x−2)3f&#x27;\left( x \right)={{x}^{4}}{{\left( x+1 \right)}^{4}}{{\left( x-2 \right)}^{3}} . Tìm số điểm cực trị của hàm số y=f(x)y=f\left( x \right)

A.0

B.1

C.2

D.3

Câu 8: Tìm tập hợp tất cả giá trị thực của tham số k để hàm số y=x33−(k2−3k)x2−12x+1y=\frac{{{x}^{3}}}{3}-\left( {{k}^{2}}-3k \right){{x}^{2}}-12x+1 đạt cực tiểu tại x=2x=2

A.{2}\left\{ 2 \right\}

B.∅\varnothing

C.{1}\left\{ 1 \right\}

D.{1,2}\left\{ 1,2 \right\}

Câu 9: Tìm tập hợp tất cả giá trị thực của tham số k để hàm số y=x33+(k2−5k)x22+(5−2k)x+2y=\frac{{{x}^{3}}}{3}+\frac{\left( {{k}^{2}}-5k \right){{x}^{2}}}{2}+\left( 5-2k \right)x+2 đạt cực tiểu tại 1

A.{1}\left\{ 1 \right\}

B.∅\varnothing

C.{6}\left\{ 6 \right\}

D.{1,6}\left\{ 1,6 \right\}

Câu 10: Tìm tập hợp tất cả giá trị thực của tham số m để hàm số y=23x3−mx2−2(3m2−1)x+23y=\frac{2}{3}{{x}^{3}}-m{{x}^{2}}-2\left( 3{{m}^{2}}-1 \right)x+\frac{2}{3} có hai điểm cực trị x1{{x}_{1}} và x2{{x}_{2}} sao cho x1x2+2(x1+x2)=1{{x}_{1}}{{x}_{2}}+2\left( {{x}_{1}}+{{x}_{2}} \right)=1

A.{0,23}\left\{ 0,\frac{2}{3} \right\}

B.{0}\left\{ 0 \right\}

C.{23}\left\{ \frac{2}{3} \right\}

D.∅\varnothing

ĐÁP ÁN

 

Bài viết gợi ý:

1. [TOÁN 12] Bài Toán Tương Giao

2. [TOÁN 11] Hàm Số Liên Tục

3. [TOÁN 11] Định Nghĩa Và Ý Nghĩa Của Đạo Hàm

4. [TOÁN 11] Đại Cương Về Phương Trình

5. [TOÁN 11] Nhị Thức Newton

6. [TOÁN 12] Giới Hạn Của Hàm Sô

7. [TOÁN 11] Phương Pháp Quy Nạp Toán Học