Bài toán thực tế liên quan đến hình học
A. Nội dung kiến thức.
Bài toán thực tế liên quan đến hình học thường xoay quanh một số nội dung như sau: Tính toán để đường đi được ngắn nhất, tính toán để diện tích được lớn nhất, hay cũng có thể đơn giản là tính diện tích hoặc thể tích của một vật…
Ta chú ý một số kiến thức sau:
1. Công thức tính chu vi, diện tích của các hình, thể tích của các khối hình.
* Hình tam giác: Cho tam giác ABC đường cao AH, đặt a = BC, b = CA, c = AB, h = AH.
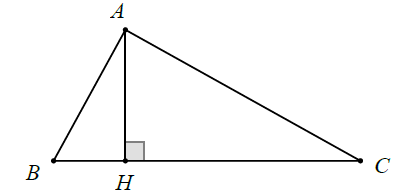
Chu vi tam giác là : P = a + b + c.
Diện tích tam giác là :
$S=\frac{1}{2}ah=\frac{1}{2}ab.\sin C=\sqrt{p(p-a)(p-b)(p-c)}$
( với $p=\frac{P}{2}$).
* Hình quạt: Xét hình quạt OAB có bán kính R, góc ở tâm bằng$\alpha $ (tính theo radian).
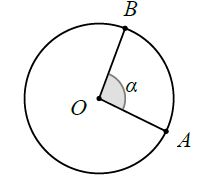
Chu vi của hình quạt là :$P=2\pi R.\frac{\alpha }{2\pi }\Leftrightarrow P=\alpha R.$
Diện tích của hình quạt là : $S=2\pi {{R}^{2}}.\frac{\alpha }{2\pi }\Leftrightarrow S=\alpha {{R}^{2}}.$
* Hình nón, khối nón:
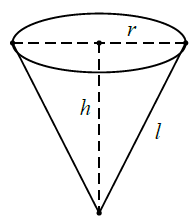
Diện tích xuang quanh của hình nón có bán kính đường tròn đáy bằng r và có độ dài đường sinh bằng l là:${{S}_{xq}}=\pi rl.$
Diện tích toàn phần của hình nón tròn xoay bằng diện tích xung quanh của hình nón cộng với diện tích đáy của hình nón:${{S}_{tp}}=\pi rl+\pi {{r}^{2}}$
Thể tích của khối nón tròn xoay có có chiều cao h và bán kính đáy bằng r là:$V=\frac{1}{3}\pi {{r}^{2}}h.$
*Hình trụ, khối trụ:
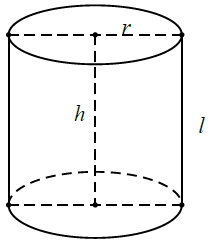
Diện tích xuang quanh của hình trụ có bán kính đáy bằng r và có đường sinh bằng l là:${{S}_{xq}}=2\pi rl.$
Diện tích toàn phần của hình trụ bằng diện tích xung quanh của hình trụ đó cộng với diện tích hai đáy của hình trụ: ${{S}_{tp}}=2\pi rl+2\pi {{r}^{2}}.$
Thể tích của khối trụ có chiều cao h và có bán kính đáy bằng r là:$V=\pi {{r}^{2}}h.$
Chú ý: Trường hợp hình lăng trụ đứng và khối lăng trụ đứng (như hình vẽ) thì h = l.
*Mặt cầu, khối cầu:
Mặt cầu bán kính R có diện tích là:$S=4\pi {{R}^{2}}.$
Khối cầu bán kính R có thể tích là: $S=\frac{4}{3}\pi {{R}^{3}}.$
2. Cách tìm giá trị lớn nhất, nhỏ nhất của hàm số trên một đoạn, khoảng, nửa đoạn, nửa khoảng.
Có lẽ đây là một bài toán khá quen thuộc với rất nhiều bạn đọc, tác giả sẽ không nhắc lại phương pháp khảo sát hàm số để tìm giá trị lớn nhất và nhỏ nhất. Tác giả cung cấp thêm cho bạn đọc một số công thức sau:
- Cho hàm số $y=a{{x}^{2}}+bx+c,$ nếu a > 0 thì hàm số đã cho đạt giá trị nhỏ nhất trên $\mathbb{R}$khi$x=\frac{-b}{2a}.$
- Cho hàm số $y=a{{x}^{2}}+bx+c,$ nếu a < 0 thì hàm số đã cho đạt giá trị lớn nhất trên $\mathbb{R}$ khi $x=\frac{-b}{2a}.$
- Với a , b là các số thực dương thì ta có: ${{\sqrt{ab}}^{AM-GM}}\le \frac{a+b}{2}\Rightarrow ab\le \frac{{{(a+b)}^{2}}}{4}$ Đẳng thức xảy ra khi a = b.
- Vớia , b, c là các số thực dương thì ta có: ${{\sqrt[3]{abc}}^{AM-GM}}\le \frac{a+b+c}{3}\Rightarrow abc\le \frac{{{(a+b+c)}^{3}}}{27}$Đẳng thức xảy ra khi a = b = c.
Phần chứng minh xin để lại cho bạn đọc.
3. Ứng dụng của tích phân trong việc tính diện tích hình phẳng, tính thể tích của khối tròn xoay.
- Nếu hàm số y = f(x) liên tục trên đoạn [ a;b] thì diện tích S của hình phẳng giới hạn bởi các đường : $y=f(x),y=0,x=a,x=b$ là $S=\int\limits_{a}^{b}{\left| f(x) \right|dx}$.
- Diện tích S của hình phẳng giới hạn bởi đồ thị các hàm số $y=f(x)=g(x)$ liên tục trên đoạn [ a; b] và hai đường thẳng x = a, x = b là $S=\int\limits_{a}^{b}{\left| f(x)-g(x) \right|dx}$
- Cho hàm số y = f(x) liên tục trên [a , b]. Thể tích V của khối tròn xoay tạo bởi hình phẳng giới hạn bởi các đường$y=f(x),y=0,x=a,x=b,$ : khi quay xung quanh trục hoành được tính theo công thức : $V=\pi \int\limits_{a}^{b}{{{f}^{2}}(x)dx.}$
- Thể tích V của khối tròn xoay tạo bởi hình phẳng giới hạn bởi các đường $y=f(x),y=g(x),(0\le f(x)\le g(x);f;g$ liên tục trên đoạn [a;b]), x = a, x = b , khi quay xung quanh trục Ox được tính theo công thức : $V=\pi \int\limits_{a}^{b}{\left| {{g}^{2}}(x)-{{f}^{2}}(x) \right|dx.}$
B. Ví dụ minh hoạ.
Ví dụ 1. Một đường dây điện được nối từ nhà máy điện trên bờ biển ở vị trí A đến vị trí C trên một hòn đảo. Khoảng cách ngắn nhất từ C đến đất liền là đoạn BC có độ dài 1 km, khoảng cách từ A đến B là 4 km. Người ta chọn một vị trí là điểm S nằm giữa A và B để mắc đường dây điện từ A đến S, rồi từ S đến C như hình vẽ dưới đây. Chi phí mỗi km dây điện trên đất liền mất 3000USD, mỗi km dây điện đặt ngầm dưới biển mất 5000USD. Hỏi điểm S phải cách điểm A bao nhiêu km để chi phí mắc đường dây điện là ít nhất.

A. 3,25 km. B. 1 km. C. 2 km. D. 1,5 km.
Lời giải
Cách 1:
Giả sử\[AS=x,0
Tổng chi phí mắc đường dây điện là : $f(x)=300x+500\sqrt{1+{{(4-x)}^{2}}}$ .
Bài toán trở thành tìm giá trị lớn nhất của $f(x)$ trên (0;4).
Đặt:$t={{x}^{2}},t>0$ . Xét: $f(t)=\frac{t+5,76}{\sqrt{t+3,24}.\sqrt{t+10,24}}=\frac{t+5,76}{\sqrt{{{t}^{2}}+13,48t+33,1776}}$
Ta có:$f'(t)=\frac{\sqrt{{{t}^{2}}+13,48t+33,1776}-\frac{t+6,74}{\sqrt{{{t}^{2}}+13,48t+33,1776}}.(t+5,76)}{{{t}^{2}}+13,48t+33,1776}$
$f'(t)=\frac{0,98t-5,6448}{{{\left( \sqrt{{{t}^{2}}+13,48t+33,1776} \right)}^{3}}}\Rightarrow f'(t)=0\Leftrightarrow t=5,76.$
Suy ra cos BOC lớn nhất khi $x=\sqrt{5,76}=2,4.$
Đáp án A.
Cách 2:
Ta có: Ta có: f (3,25) =1600; f (1) =1881,13883; f (2) =1718,033989; f (1,5) =1796,291202.
Như vậy ta cũng tìm ra A là đáp án.
Bình luận: Không ít bạn đọc cho rằng cách giải thứ hai không được khoa học và làm mất đi vẻ
đẹp của toán học. Quan điểm của tác giả về Cách 1 và Cách 2 như sau:
- Cả hai cách đều phải tìm giá trị lớn nhất của f (x) trên (0;4).
- Cách 1: Chúng ta giải quyết bằng cách khảo sát hàm số f (x) trên khoảng (0;4) để tìm ra
giá trị của x mà tại đó f (x) đạt giá trị lớn nhất; tiếp theo, so sánh kết quả tìm được với các
đáp án A, B, C, D để tìm ra câu trả lời đúng cho câu hỏi.
- Cách 2: Sau khi lập được hàm số f (x) như Cách 1, tính f (3,25), f (1), f (2), f (1,5); số
lớn nhất trong bốn số tính được sẽ là giá trị lớn nhất của f (x). Từ đó, hiển nhiên, dễ dàng
tìm ra câu trả lời đúng cho câu hỏi.
Có thể thấy, rõ ràng Cách 2 giúp ta tìm đáp án nhanh hơn cách 1. Sự khác biệt giữa Cách 1 và Cách 2 nêu trên nằm ở quan niệm về tình huống đặt ra. Với Cách 1, ta coi các phương
án A, B, C, D chỉ là các dữ liệu đưa ra để đối chiếu; với Cách 2, ta coi các phương án A, B, C, D là giả thiết của tình huống đặt ra.
- Có lẽ những bài tập trắc nghiệm có thể làm theo Cách 2 đôi phần là hạn chế của việc kiểm tra
theo hình thức trắc nghiệm, tuy nhiên trong quá trình làm bài thi mỗi câu hỏi đã được người ra đề đã ngầm ấn định khoảng thời gian làm bài, do vậy theo tác giả nếu gặp câu hỏi này trong phòng thi học sinh nên làm theo Cách 2.
Ví dụ 2. Một màn hình ti vi hình chữ nhật cao 1,4 m được đặt ở độ cao 1,8 m so với tầm mắt (tính từ đầu mép dưới của màn hình). Để nhìn rõ nhất phải xác định vị trí đứng sao cho góc nhìn lớn nhất ( là góc nhìn). Hãy xác định độ dài AO để nhìn được rõ nhất. BOC
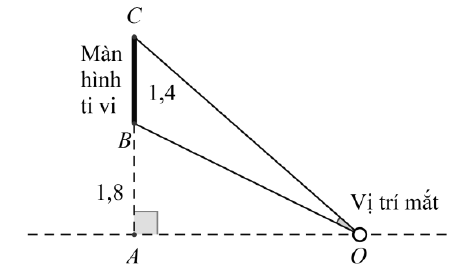
A. AO = 2,4 m. B. AO = 2 m. C. AO = 2,6 m. D. AO = 3 m.
Lời giải
Đặt :$AO=x,(x>0)\Rightarrow OB=\sqrt{{{x}^{2}}+3,24},OC=\sqrt{{{x}^{2}}+10,24}.$ Ta có:\[cosBOC=\frac{O{{B}^{2}}+O{{C}^{2}}-B{{C}^{2}}}{2OB.OC}=\frac{{{x}^{2}}+3,24+{{x}^{2}}+10,24-1,96}{2\sqrt{{{x}^{2}}+3,24}.\sqrt{{{x}^{2}}+10,24}}=\frac{{{x}^{2}}+5,76}{\sqrt{{{x}^{2}}+3,24}.\sqrt{{{x}^{2}}+10,24}}\]
Góc nhìn BOC lớn nhất khi bé nhất. cosBOC
Cách 1:
Đặt:$t={{x}^{2}},t>0$ . Xét: $f(t)=\frac{t+5,76}{\sqrt{t+3,24}.\sqrt{t+10,24}}=\frac{t+5,76}{\sqrt{{{t}^{2}}+13,48t+33,1776}}$
Ta có:$f'(t)=\frac{\sqrt{{{t}^{2}}+13,48t+33,1776}-\frac{t+6,74}{\sqrt{{{t}^{2}}+13,48t+33,1776}}.(t+5,76)}{{{t}^{2}}+13,48t+33,1776}$
$f'(t)=\frac{0,98t-5,6448}{{{\left( \sqrt{{{t}^{2}}+13,48t+33,1776} \right)}^{3}}}\Rightarrow f'(t)=0\Leftrightarrow t=5,76.$
Suy ra cos BOC lớn nhất khi $x=\sqrt{5,76}=2,4.$
Đáp án A.
Cách 2:
Ta sẽ thử xem trong 4 đáp án đã cho đáp án nào làm nhỏ nhất thì đó là đáp án cần tìm. cosBOC
Đặt:$f(x)=\frac{{{x}^{2}}+5,76}{\sqrt{{{x}^{2}}+3,24}.\sqrt{{{x}^{2}}+10,24}}$ .Ta có:
$f(2,4)=\frac{24}{25}=0,96;f(2)=0,9612260675;f(2,6)=0,960240166;f(3)=0,960240166.$
Từ đó suy ra A là đáp án.







