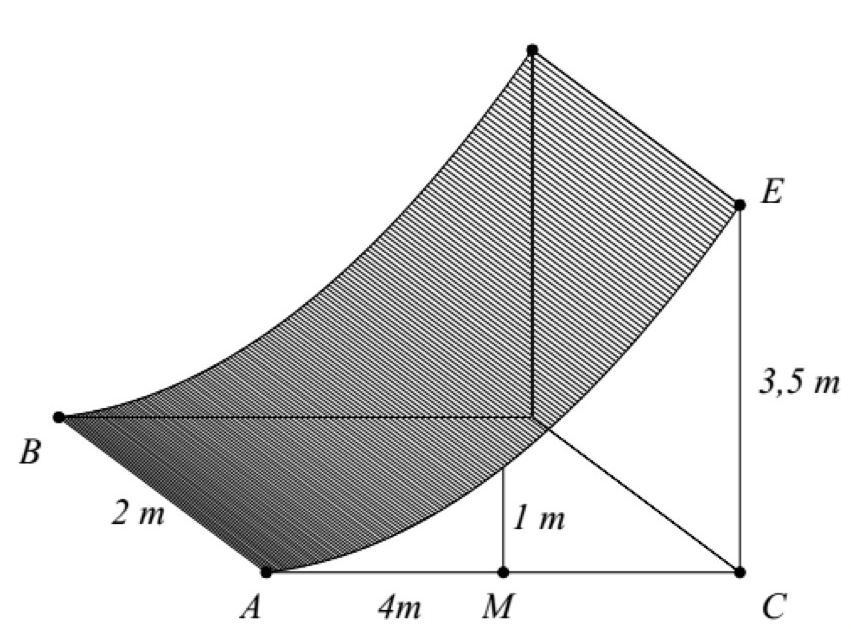
Bài 1: Chướng ngại vật “tường cong” trong một sân thi đấu X - Game là một khối bê tông có chiều cao từ mặt đất lên là 3,5m.Giao của mặt tường cong và mặt đất là đoạn thẳng $AB=2m.$ Thiết diện của khối tường cong cắt bởi mặt phẳng vuông góc với ABtại Alà một hình tam giác vuông cong ACEvới $AC=4m,\,CE=3,5\,m$ và cạnh cong $AE$ nằm trên một đường parabol có trục đối xứng vuông góc với mặt đất. Tại vị trị Mlà trung điểm của ACthì tường cong có độ cao 1m(xem hình minh họa bên). Tính thể tích bê tông cần sử dụng để tạo nên khối tường cong đó.
A. $9,75\,{{m}^{3}}$ B. $10,5\,{{m}^{3}}$C. $10\,{{m}^{3}}$ D. $10,25\,\,{{m}^{3}}$
Giải. Đặt gốc tọa độ ngay tại \[A\] và\[Ox\] trùng với \[AC,\] trục \[Oy\]qua \[A\] và song song \[CE\].
Ta có phương trình parabol qua các điểm \[A(0;0),N(2;1),E\left( 4;\frac{7}{2} \right)\] là: \[y=\frac{3}{16}{{x}^{2}}+\frac{1}{8}x.\]
Khi đó diện tích tam giác vuông cong \[ACE\] là \[\int\limits_{0}^{4}{\left( \frac{3}{16}{{x}^{2}}+\frac{1}{8}x \right)}dx=5\left( {{m}^{2}} \right).\]
Vậy thể tích bê tông cần để tạo nên tường cong đó là \[2.5=10\left( {{m}^{3}} \right).\]Chọn đáp án C.
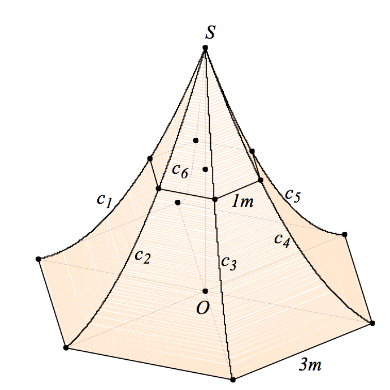
Bài 2:Người ta dựng một cái lều vải (H) có dạng hình “chóp lục giác cong đều” như hình vẽ bên. Đáy của (H) là một hình lục giác đều cạnh $3m.$ Chiều cao $SO=6m$ (SO vuông góc với mặt phẳng đáy). Các cạnh bên của (H) là các sợi dây ${{c}_{1}},\,{{c}_{2}},\,{{c}_{3}},\,{{c}_{4}},\,{{c}_{5}},\,{{c}_{6}}$ nằm trên các đường parabol có trục đối xứng song song với SO. Giả sử giao tuyến (nếu có) của (H) với mặt phẳng (P) vuông góc với SO là một lục giác đều và khi (P) qua trung điểm của SO thì lục giác đều có cạnh bằng $1m.$ Tính thể tích phần không gian nằm bên trong cái lều (H) đó.
A. $\frac{135\sqrt{3}}{5}\,\,({{m}^{3}})$
B. $\frac{96\sqrt{3}}{5}\,\,({{m}^{3}})$
C. $\frac{135\sqrt{3}}{4}\,\,({{m}^{3}})$
D. $\frac{135\sqrt{3}}{8}\,\,({{m}^{3}})$
Giải. Chọn trục toạ độ $Oy$ trùng với $OS$ và $Ox$ trùng với $O{{A}_{1}}.$
Phương trình đường cong parabol ${{c}_{1}}$ là $y=a{{x}^{2}}+bx+c$ đi qua các điểm $(0;6),(3;0),(1;3).$ Do đó $\left\{ \begin{aligned} & c=6 \\ & 9a+3b+c=0 \\ & a+b+c=3 \\ \end{aligned} \right.\Leftrightarrow a=\frac{1}{2},b=-\frac{7}{2},c=6\Rightarrow y=\frac{1}{2}{{x}^{2}}-\frac{7}{2}x+6.$
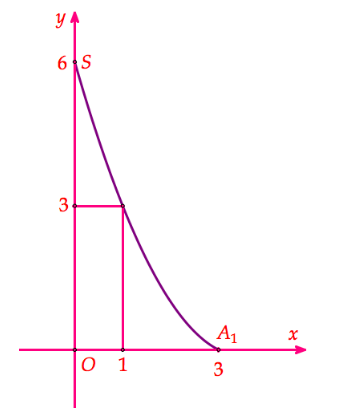
Khi cắt $(H)$ bởi mặt phẳng vuông góc với trục $Oy$ tại điểm có tung độ $y(0\le y\le 6)$ ta được thiết diện là một hình lục giác đều có độ dài cạnh $x$ xác định bởi $y=\frac{1}{2}{{x}^{2}}-\frac{7}{2}x+6.$
Do đó $x=\frac{7\pm \sqrt{1+8y}}{2}$ với $0\le x\le 3$ nên $x=\frac{7-\sqrt{1+8y}}{2}.$
Do đó diện tích thiết diện là $S=6.\frac{{{x}^{2}}\sqrt{3}}{4}=\frac{3\sqrt{3}}{2}{{\left( \frac{7-\sqrt{1+8y}}{2} \right)}^{2}}.$
Và thể tích của $(H)$ là $V=\int\limits_{0}^{6}{Sdy}=\int\limits_{0}^{6}{\frac{3\sqrt{3}}{2}{{\left( \frac{7-\sqrt{1+8y}}{2} \right)}^{2}}dy}=\frac{135\sqrt{3}}{8}({{m}^{3}}).$
*Chú ý. Ở đây chọn trục $Oy$ trùng với $OS$ vì đề bài cho trục đối xứng của các đường parabol song song với $OS.$







