TÓM TẮT LÝ THUYẾT
1. SỐ MŨ
1.1. Định nghĩa:
Số mũ | Định nghĩa | Điều kiện | Ví dụ |
\[n\in {{\mathbb{Z}}^{+}}\], n>1 | \[{{a}^{n}}=a.a......a\](n thừa số) | \[a\in \mathbb{R}\] | \[{{3}^{2}}=3.3=9\] |
n=1 | \[{{a}^{1}}=a\] | \[{{5}^{1}}=5\] | |
n=0 | \[{{a}^{0}}=1\] | \[a\ne 0\] | \[{{5}^{0}}=1\] |
\[n\in {{\mathbb{Z}}^{+}}\] | \[{{a}^{-n}}=\frac{1}{{{a}^{n}}}\] | \[a\ne 0\] | \[{{2}^{-3}}=\frac{1}{{{2}^{3}}}=\frac{1}{8}\] |
\[\frac{m}{n}\in {{\mathbb{Q}}^{+}}\] | \[{{a}^{\frac{m}{n}}}=\sqrt[n]{{{a}^{m}}}\] | a>0 | \[{{8}^{\frac{2}{3}}}=\sqrt[8]{{{8}^{2}}}=4\] |
1.2. Tính chất cần nhớ
\[{{a}^{m}}.{{a}^{n}}={{a}^{m+n}}\] | \[\frac{{{a}^{n}}}{{{b}^{n}}}={{\left( \frac{a}{b} \right)}^{n}}\] |
\[\frac{{{a}^{m}}}{{{a}^{n}}}={{a}^{m+n}}\] | \[{{\left( \frac{a}{b} \right)}^{-n}}={{\left( \frac{b}{a} \right)}^{n}}\] |
\[{{({{a}^{m}})}^{n}}={{a}^{m.n}}\] | \[\sqrt[n]{a}.\sqrt[n]{b}=\sqrt[n]{ab}\] |
\[\sqrt[m.n]{{{a}^{n}}}=\sqrt[m]{a}\] | \[\frac{\sqrt[n]{a}}{\sqrt[n]{b}}=\sqrt[n]{\frac{a}{b}}\] |
\[{{a}^{n}}{{b}^{n}}={{(ab)}^{n}}\] | \[\sqrt[m]{\sqrt[n]{a}}=\sqrt[m.n]{a}\] |
1.3. So sánh:
· Với a > 1, ap > aq $\Leftrightarrow $p > q
· Với 0 < a < 1, ap > aq $\Leftrightarrow $p < q
· Với 0 < a < b và m là số nguyên thì
+ am < bm $\Leftrightarrow $ m > 0
+ am > bm $\Leftrightarrow $ m < 0
+a, b > 0: an = b n $\Leftrightarrow $ a = b
· Với n là nguyên dương lẻ và a < b thì $\sqrt[n]{a}<\sqrt[n]{b}$
· Với n là nguyên dương chẵn và 0 < a < b thì $\sqrt[n]{a}<\sqrt[n]{b}$
2. LOGARIT
2.1. Định nghĩa: cho a > 0, a \[\ne \]1, b>0
\[{{\log }_{a}}b=x,x\in \mathbb{R}\Leftrightarrow {{a}^{x}}=b\]
Vd: \[{{\log }_{2}}8=3\]
\[{{\log }_{2}}\sqrt{2}=\frac{1}{2}\]
2.2. Tính chất:
\[{{\log }_{a}}1=0\] \[{{\log }_{a}}a=1\]
\[{{\log }_{a}}({{a}^{n}})=n\] \[{{a}^{{{\log }_{a}}n}}=n\]
\[{{\log }_{a}}u+{{\log }_{a}}v={{\log }_{a}}(uv)\]
\[{{\log }_{a}}u-{{\log }_{a}}v={{\log }_{a}}\left( \frac{u}{v} \right)\]
\[{{\log }_{a}}b={{\log }_{{{a}^{n}}}}({{b}^{n}})={{\log }_{\sqrt[n]{a}}}\left( \sqrt[n]{b} \right)\]
\[{{\log }_{{{a}^{\alpha }}}}({{b}^{\beta }})=\frac{\beta }{\alpha }{{\log }_{a}}b\]
(*) Công thức đổi cơ số
\[{{\log }_{a}}b=\frac{1}{{{\log }_{b}}a}\] \[{{\log }_{a}}b=\frac{1}{{{\log }_{b}}a}\] \[{{\log }_{a}}b=\frac{{{\log }_{c}}a}{{{\log }_{c}}b}\]
\[{{\log }_{a}}(b).{{\log }_{b}}(a)=1\] \[{{\log }_{a}}(b).{{\log }_{b}}(c)={{\log }_{a}}c\]
2.3. So sánh:
• Khi a > 1 thì \[{{\log }_{a}}\]b > \[{{\log }_{a}}\]c $\Leftrightarrow $ b > c > 0
• Khi 0 < a < 1 thì \[{{\log }_{a}}\]b > \[{{\log }_{a}}\]c $\Leftrightarrow $ 0 < b < c
2.4. Đặc biệt:
2.4.1. Logarit tự nhiên
\[{{\log }_{e}}b=\ln b\] với \[e\approx 2.71828...\]
2.4.2. Logarit thập phân
\[{{\log }_{10}}b=\log b\]
3. HÀM SỐ MŨ, HÀM SỐ LOGARIT
Hàm số mũ, \[y={{a}^{x}}\] | Hàm số logarit, \[y={{\log }_{a}}x\] | |
1) ĐK | a>0,a \[\ne \]1 | \[a>0,a\ne 1\] |
2) TXĐ | \[D=\mathbb{R}\] | $$D = (0; + \infty )$$ |
3) Tập giá trị | $$Y = (0; + \infty )$$ | \[Y=\mathbb{R}\] |
4) Miền liên tục | \[\mathbb{R}\] | $$(0; + \infty )$$ |
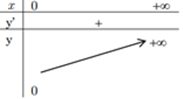
5) bảng biến thiên | 0<>
a>1
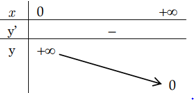
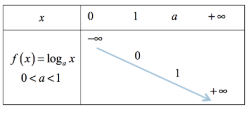
| 0<>
a>1
|
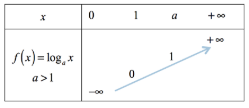
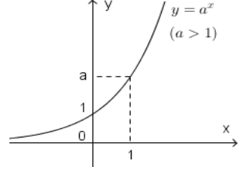
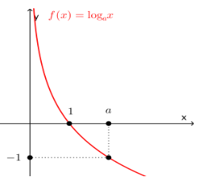
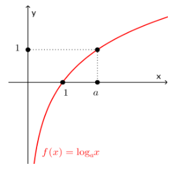
6) đồ thị | 0<> a>1
| 0<>
a>1
|
7) đạo hàm | $$({a^x})' = {a^x}\ln a$$ $$({e^x})' = {e^x}$$ $$({a^u})' = u'{a^u}{\mathop{\rm lna}\nolimits} $$ $$({e^u})' = u'{e^u}$$ $$({e^{kx}})' = k{e^{kx}}$$ | (lnx)’ = \[\frac{\text{1}}{\text{x}}\] \[{{\text{(lo}{{\text{g}}_{\text{a}}}\text{x)}}^{\text{ }\!\!'\!\!\text{ }}}=\frac{\text{1}}{\text{x}\text{.lna}}\] |
4. HÀM LUỸ THỪA y = xa (a ÎR)
• Hàm số y = xa có TXĐ D = (0; +$\infty $)
Trừ các trường hợp sau:
+ Nếu a nguyên dương thì TXĐ D = R
+ Nếu a nguyên âm hoặc a = 0 thì hàm số có TXĐ là D = R\{0}
• Hàm số y = xa (Với a ≠ 0)
+Đồng biến trên khoảng (0; +$\infty $) nếu a > 0
+Nghịch biến trên (0; +$\infty $) nếu a < 0.
• Đồ thị của hàm số luôn đi qua điểm (1; 1).
• Đạo hàm:
$${\left( {{x^a}} \right)^\prime } = a.{x^{a - 1}}$$
\[{{\text{(}\frac{\text{1}}{\text{x}}\text{)}}^{\text{ }\!\!'\!\!\text{ }}}=-\frac{\text{1}}{{{\text{x}}^{\text{2}}}}\]
\[{{\text{(}\sqrt{\text{x}}\text{)}}^{\text{ }\!\!'\!\!\text{ }}}=\frac{\text{1}}{\text{2}\sqrt{\text{x}}}\]