MÃ ĐỀ 101 (TỪ CÂU 35 ĐẾN 50) GIẢI CHI TIẾT VÀ NHẬN XÉT
Nhận xét chung: Trong 16 câu (01 vận dụng thấp và
15 câu vận dụng cao) này không cần phải tính toán nhiều. Các câu chỉ trải qua
nhiều nhất là khoảng 3 bước tính toán đơn giản (cộng, trừ, nhân, chia). Chủ yếu
trong 16 câu này là kiểm tra về tư duy toán học, việc nắm kiến thức của học
sinh có chắc chắn, sâu sắc và đủ rộng không. So với đề thi năm 2017, mức độ tính toán ở 16 câu cuối giảm đi 50%
nhưng mức độ tư duy thì nặng gấp đôi. Điều này có lợi cho các học sinh nắm kiến
thức sâu sắc và tư duy sáng sủa, nhưng lại gây khó khăn cho các học sinh học
theo hình thức thuộc bài và thiên về tính toán.
Câu
35: Có bao nhiêu giá trị nguyên của $m$ để hàm số $y=\frac{x+2}{x+5m}$
đồng biến trên $\left( -\infty ;-10 \right)$?
LG: Ta có ${y}'=\frac{5m-2}{{{\left( x+5m \right)}^{2}}}$. Từ dáng điệu hàm phân thức ta thấy
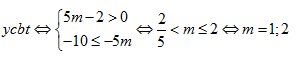
Vậy có 2 giá trị nguyên của $m$ thỏa mãn.
Nhận
xét. Đây là câu ở mức vận dụng thấp, được cho nhẹ
nhàng và đẹp, nhưng học sinh không vững kiến thức về nhận biết đồ thị vẫn không
làm được.
Câu
36: Có bao nhiêu giá trị nguyên của tham số $m$ để
hàm số $y={{x}^{8}}+\left( m-2 \right){{x}^{5}}-\left( {{m}^{2}}-4
\right){{x}^{4}}+1$ đạt cực tiểu tại $x=0$?
LG: Ta có ${y}'=8{{x}^{7}}+5\left( m-2 \right){{x}^{4}}-4\left( {{m}^{2}}-4 \right){{x}^{3}}$. Vậy
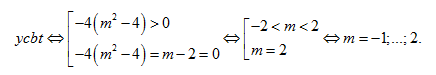
Vậy có 4 giá trị nguyên của $m$ thỏa mãn.
Nhận
xét. Ở đây phải nhận
thấy hàm đạt cực tiểu tại $x=0$ thì tương đương với ${y}'\left( 0 \right)=0$ và
${y}'=\left( x \right)$ đổi dấu tử âm sang dương khi $x$ chạy qua điểm 0 (từ âm
sang dương), điều này lại tương đương với số hạng chứa lũy thừa thấp nhất của $x$
có hệ số khác không trong biểu thức ${y}'$ phải là lũy thừa bậc lẻ và hệ số
dương. Đây là bước tư duy không tầm thường, học sinh phải hiểu thật sâu sắc kiến
thức.
Câu
37: Cho hình lập phương $ABCD.{A}'{B}'{C}'{D}'$ có
tâm $O$. Gọi $I$ là tâm hình vuông ${A}'{B}'{C}'{D}'$ và $M$ là điểm thuộc đoạn
$OI$ sao cho $MO=2MI$. Khi đó cosin góc tạo bởi 2 mặt phẳng $\left( M{C}'{D}'
\right)$ và $\left( MAB \right)$ bằng?
LG.
Ta coi cạnh hình vuông bằng 6. Lấy $P,Q$ là trung điểm $AB$ và ${C}'{D}'$. Góc
cần tính là góc tạo bởi 2 véctơ $\overrightarrow{MP}$ và $\overrightarrow{MQ}$.
Xét mặt phẳng tọa độ gốc $I$, 2 trục là $IQ,\,IO$. Khi đó
$\overrightarrow{MQ}=\left(
3;-1 \right),\,\overrightarrow{MP}=\left( -3;5 \right);\,\cos \alpha
=\frac{\left| -9;-5
\right|}{\sqrt{{{3}^{2}}+1}\sqrt{{{3}^{2}}+{{5}^{2}}}}=\frac{14}{\sqrt{10}\sqrt{34}}=\frac{7\sqrt{85}}{85}.$
Nhận
xét: Đây là bài hình không gian cơ bản, tuy nhiên: học
sinh có tư duy tốt thì sẽ làm rất ngắn gọn và không mất nhiều thời gian, ngược
lại, sẽ phải tính toán nhiều hơn.
Câu
38: Có bao nhiêu số phức $z$ thỏa mãn $\left| z
\right|\left( z-4-i \right)+2i=\left( 5-i \right)z$?
LG.
Dễ thấy phương trình đã cho tương đương với $z=\frac{4\left| z \right|+\left(
\left| z \right|-2 \right)i}{\left| z \right|-5+i}$ (*). Lấy môđun 2 vế ta được
${{\left|
z \right|}^{2}}=\frac{16{{\left| z \right|}^{2}}+{{\left( \left| z \right|-2
\right)}^{2}}}{{{\left( \left| z \right|-5 \right)}^{2}}+1}\Leftrightarrow
{{\left| z \right|}^{4}}-10{{\left| z \right|}^{3}}+9{{\left| z
\right|}^{2}}+4\left| z \right|-4=0$
Học sinh có thể bấm máy để thấy phương trình cuối
cùng có đúng 3 nghiệm dương, hoặc tách một nhân tử $\left( \left| z \right|-1
\right)$ và khảo sát nhân tử bậc 3 còn lại có hai nghiệm dương khác nữa. Thay
vào (*) thì được 3 số phức
Nhận
xét: Bài toán này học sinh nắm chắc kiến thức mới nhận
thấy mỗi nghiệm $\left| z \right|>0$ của phương trình cuối sẽ cho ra đúng 1
và chỉ 1 nghiệm $z$ của phương trình đầu thông qua mối liên hệ (*). Ngược lại nếu
học sinh đặt $z=x+yi$ sẽ rất khó khăn để làm.
Câu 39: Trong không
gian $Oxyz$, cho $\left( S \right):{{\left( x+1 \right)}^{2}}+{{\left( y+1
\right)}^{2}}+{{\left( z+1 \right)}^{2}}=9$ và điểm $A\left( 2;3;-1 \right)$.
Xét các điểm $M$ trên $\left( S \right)$ sao cho $AM$ tiếp xúc với $\left( S
\right)$. Khi đó $M$ luôn thuộc mặt phẳng?
LG. Tâm mặt cầu $I\left(
-1;-1;-1 \right)$. $A{{I}^{2}}=25,A{{M}^{2}}=A{{I}^{2}}-9=16$ vậy $M$ thuộc vào
mặt cầu
$\left( {{S}'}
\right):{{\left( x-2 \right)}^{2}}+{{\left( y-3 \right)}^{2}}+{{\left( z+1
\right)}^{2}}=16.$
Lấy
phương trình của $\left( S \right)$ trừ đi phương trình của $\left( {{S}'}
\right)$ (tương ứng vế với vế) ta được phương trình của mặt phẳng luôn chứa $M$
là
$6x+8y-11=-7\Leftrightarrow
3x+4y-2=0.$
Nhận xét:
Tọa độ không gian luôn là phần dễ nhất, nhưng yêu cầu đối với học sinh bày này
chỉ là tư duy tưởng tượng hình, việc tính toán gần như không đáng kể.
Câu
40: Cho hàm số $y=\frac{1}{4}{{x}^{4}}-\frac{7}{2}{{x}^{2}}$.
Có bao nhiêu điểm $A$ thuộc đồ thị hàm số sao chi tiếp tuyến tại $A$ cắt lại đồ
thị tại hai điểm khác $A$ là $M\left( {{x}_{1}};{{y}_{1}} \right),N\left(
{{x}_{2}};{{y}_{2}} \right)$ thỏa mãn ${{y}_{1}}-{{y}_{2}}=6\left(
{{x}_{1}}-{{x}_{2}} \right)$.
LG: Chú ý ${y}'={{x}^{3}}-7x=0\Leftrightarrow x=-\sqrt{7};0;\sqrt{7};$ và ${{y}'}'=3{{x}^{2}}-7$. Ta thấy hàm số đã cho là hàm trùng phương bậc 4 hướng lên trên, vậy 1 điểm $A\left( {{x}_{0}};{{y}_{0}} \right)$ mà tiếp tuyến tại đó có đúng 3 điểm chung với đồ thị khi và chỉ khi ${{x}_{CT1}}<{{x}_{0}}<{{x}_{CT2}}$ và ${{x}_{0}}$ không là nghiệm kép của phương trình tương giao, hay ${{y}'}'\left( {{x}_{0}} \right)\ne 0$. Còn điều kiện còn lại tương đương với hệ số góc của tiếp tuyến ${y}'\left( {{x}_{0}}=6 \right)$. Vậy
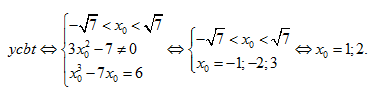
Vậy có 2 điểm $A$.
Nhận
xét: thực tế điều kiện ${{y}'}'\left( {{x}_{0}}
\right)\ne 0$ trong bài này không cần kiểm tra vì phương trình hệ số góc bằng 6
không có nghiệm $\pm \sqrt{\frac{7}{3}}$. Do vậy ngay cả khi học sinh quên điều
kiện này thì vẫn làm được. Bài toán sẽ trở lên rất khó và nhiều em làm sai nếu
nghiệm của phương trình ${y}'=6$ thỏa mãn phương trình ${{y}'}'=0$.
Câu
41: Cho hàm số $f\left( x
\right)=a{{x}^{3}}+b{{x}^{2}}+cx-\frac{1}{2}$ và $g\left( x
\right)=d{{x}^{2}}+ex+1$. Biết đồ thị hàm số $y=f\left( x \right);y=g\left( x
\right)$ cắt nhau tại 3 điểm có hoành độ $-3;-1;1$. Hình phẳng giới hạn bởi đồ
thị hai hàm số bằng?
LG:
Ta có $f\left( x \right)-g\left( x \right)=m\left( x+3 \right)\left( x+1
\right)\left( x-1 \right)$ với $-3m=f\left( 0 \right)-g\left( 0
\right)=-\frac{3}{2}$. Vậy
$dtich=\left|
\int\limits_{-3}^{-1}{\frac{1}{2}\left( x+3 \right)\left( {{x}^{2}}-1
\right)dx-\int\limits_{-1}^{1}{\frac{1}{2}\left( x+3 \right)\left( {{x}^{2}}-1
\right)dx}} \right|=4$.
Nhận
xét: Bài này nếu học sinh sử dụng cách thay từng nghiệm
vào để tìm các hệ số của $f-g$ thì vẫn được. Tuy nhiên sẽ mất nhiều thời gian.
Học sinh khá giỏi sẽ tư duy như trên và không mất công tính toán (bước tích
phân học sinh có thể bấm máy). Việc cho hình minh họa trong bài này là một điểm
không hay, vì sẽ hướng học sinh đến việc dựng lại hàm $f$ và $g$.
Câu
42: Cho khối lăng trụ $ABC.{A}'{B}'{C}'$, khoảng
cách từ $C$ đến đường thẳng $B{B}'$ bằng 2, khoảng cách từ $A$ đến $B{B}'$ và $C{C}'$lần
lượt bằng $1$ và $\sqrt{3}$, hình chiếu vuông góc của $A$ lên mặt phẳng $\left(
{A}'{B}'{C}' \right)$ là trung điểm $M$ của ${B}'{C}',{A}'M=\frac{2\sqrt{3}}{3}$.
Thể tích khối lăng trụ đã cho bằng?
LG.
Mặt phẳng qua $M$ vuông góc với cạnh bên khối lăng trụ cắt $A{A}',B{B}',C{C}'$
tại${{A}_{1}},{{B}_{1}},{{C}_{1}}$. khi đó tam giác ${{A}_{1}}{{B}_{1}}{{C}_{1}}$
là thiết diện ngang của khôi lăng trụ và là tam giác vuông có hai cạnh bên $1;\sqrt{3}$
và cạnh đáy 2, đường trung tuyến là ${{A}_{1}}M=1$ (một nửa cạnh đáy). Do đó
$A{A}'=\frac{{A}'{{M}^{2}}}{{{A}_{1}}{A}'}=\frac{{A}'{{M}^{2}}}{\sqrt{{A}'{{M}^{2}}-{{A}_{1}}{{M}^{2}}}}=\frac{4/3}{\sqrt{4/3-1}}=\frac{4}{\sqrt{3}};V=A{A}'.{{S}_{{{A}_{1}}{{B}_{1}}{{C}_{1}}}}=\frac{4}{\sqrt{3}}.\frac{1}{2}.1.\sqrt{3}=2.$
Nhận
xét: Đây là bài tính thể tích dựa trên ý tưởng nguyên
thủy: số đo thể tích bằng số đo diện tích thiết diện ngang nhân với độ dài đường
sinh. Tuy nhiên nếu học sinh không nhìn ra ý tưởng này (từ việc cho khoảng cách
giữa các đường sinh) mà dựng hình, tính chiều cao thì sẽ rất phức tạp.
Câu
43: Ba bạn $A;B;C$ viết ngẫu nhiên 1 số tự nhiên thuộc
đoạn $\left[ 1;17 \right]$. Xác xuất để tổng 3 số viết ra chia hết cho 3 là
LG:
Chia tập hợp các số tự nhiên $\left[ 1;17 \right]$ hình thành 3 nhóm đồng dư
theo modun 3. Có 2 nhóm 6 phần tử, 1 nhóm 5 phần tử. Ba số được viết ra có tổng
chia hết cho 17 khi và chỉ khi cùng thuộc 1 nhóm hoặc thuộc 3 nhóm khác nhau. Vậy
xác xuất bằng
$\frac{{{2.6}^{3}}+{{5}^{3}}+3!.6.6.5}{{{17}^{3}}}=\frac{1637}{4913}.$
Nhận xét: đây là bài xác xuất nhẹ nhàng
đơn giản, không phải tính toán. Tuy nhiên kết hợp với 1 chút số học nên sẽ gây
ra lúng túng cho không ít học sinh. Học sinh có tư duy tốt mới nhận ra được. Việc
chia lớp đồng dư mang hơi hướng của toán cao cấp.
Câu
44: Cho $a>0,b>0$ thỏa mãn ${{\log
}_{3a+2b+1}}\left( 9{{a}^{2}}+{{b}^{2}}+1 \right)+{{\log }_{6ab+1}}\left(
3a+2b+1 \right)=2$. Giá trị của $a+2b$ bằng?
LG:
Sử dụng bất đẳng thức Cauchy cho 2 số ta dễ thấy
$VP\ge {{\log }_{3a+2b+1}}\left( 6ab+1 \right)+{{\log }_{6ab}}\left( 3a+2b+1 \right)\ge 2\sqrt{{{\log }_{3a+2b+1}}\left( 6ab+1 \right).{{\log }_{6ab}}\left( 3a+2b+1 \right)}=2.$
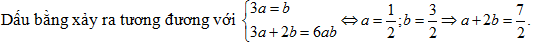
Nhận
xét: Mặc dù ở câu số 44, nhưng đây là câu dễ nhất
trong mức vận dụng cao vì bất đẳng thức Cauchy bị lộ ngay khi xuất hiện $\left(
3a+2b+1 \right)$ trong cả hai số hạng. Nhưng phần lớn học sinh không nghĩ đến việc
dùng bất đẳng thức Cauchy vì nó nằm trong chương trình lớp 10 THPT.
Câu
45: Cho hàm số $y=\frac{x-1}{x+2}$ có đồ thị $\left(
C \right)$. Gọi $I$ là giao điểm của hai đường tiệm cận của $\left( C \right)$.
Xét tam giác đều $ABI$ có hai đỉnh thuộc $\left( C \right)$. Đoạn thẳng $AB$ có
độ dài bằng?
LG:
Ta thấy $\left( C \right):y=1-\frac{3}{x+2}\Leftrightarrow
Y=-\frac{3}{{{X}'}}\left( Y=y-1;X=x+2 \right)$. Trong tọa độ mới (tịnh tiến tọa
độ không làm thay đổi độ dài vecto) $I\left( 0;0 \right)$. Do $\left( C
\right)$ là hyperbol thuộc góc 2 và 4, nên hai đỉnh $A,B$ không thể thuộc về
hai nhánh khác nhau của $\left( C \right)$ mà phải cùng thuộc về 1 nhánh và đối
xứng qua đường phân giác của góc tọa độ thứ 2 (trong hệ $IXY$). Vậy nếu $A\left(
X;Y \right)$ thì $B\left( -Y;-X \right)$ và
$I{{A}^{2}}=A{{B}^{2}}\Rightarrow {{X}^{2}}+{{Y}^{2}}=2{{\left(
X+Y \right)}^{2}}=2{{X}^{2}}+2{{Y}^{2}}-12\Rightarrow
A{{B}^{2}}={{X}^{2}}+{{Y}^{2}}=12\Rightarrow AB=2\sqrt{3.}$
Nhận
xét: Tương tự bài 35 (thuộc mức vận dụng thấp), bài
này kiểm tra về dáng điệu của hàm bậc nhất trên bậc nhất nhưng ở mức cao hơn là
tính đối xứng của đồ thị. Học sinh không nắm chắc kiến thức vẫn có thể làm được
bằng phương pháp tính toán cồng kềnh. Khi nắm được bản chất thì sẽ đưa ra lời
giải ngắn gọn như trên.
Câu 46: Cho phương trình ${{5}^{x}}+m={{\log }_{5}}\left( x-m \right)$, với $m$ là tham số. Có bao nhiêu giá trị nguyên của $m$ thuộc $\left( -20;20 \right)$ để phương trình có nghiệm?
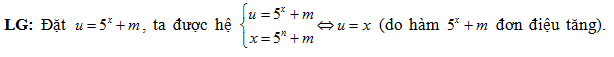
Vậy phương trình đã cho tương đương với $m=x-{{5}^{x}}=f\left(
x \right)$. Ta có ${f}'\left( x \right)=1-\left( \ln 5
\right){{.5}^{x}}=0\Leftrightarrow x={{\log }_{5}}\left( 1/\ln 5 \right)$.
Từ đó dễ thấy ${{f}_{\max }}=f\left( {{\log
}_{5}}\left( 1/\ln 5 \right) \right)\in \left( -1;0 \right);ycbt\Leftrightarrow
m\le {{f}_{\max }}$. Vậy $m=-19;...;-1$.
Do đó có 19 giá trị của $m$.
Nhận
xét: Đây là dạng bài sử dụng tính đơn điệu của hàm số
kết hợp với tính toán hàm logarit. Nói chung đây là kiểu bài quen thuộc. Sau
bài 47 thì đây là bài dễ nhất vì mức độ đòi hỏi tư duy ít.
Câu
47: Trong không gian $Oxyz$, cho mặt cầu $\left( S
\right)$ có tâm $I\left( -2;1;2 \right)$ và đi qua điểm $A\left( 1;-2;-1
\right)$. Xét các điểm $B,C,D$ thuộc $\left( S \right)$ sao cho $AB,AC,AD$ đôi
một vuông góc với nhau. Thể tích của khối tứ diện $ABCD$ có giá trị lớn nhất bằng?
LG:
Đặt $a=AB,b=AC,c=AD$. Khi đó $A{{I}^{2}}={{3}^{2}}+{{3}^{2}}+{{3}^{2}}=27.$
${{a}^{2}}+{{b}^{2}}+{{c}^{2}}={{\left(
2R \right)}^{2}}=4A{{I}^{2}}=108;\,V=\frac{abc}{6}\le \frac{{{\left(
{{a}^{2}}+{{b}^{2}}+{{c}^{2}}
\right)}^{3/2}}}{{{\sqrt{3}}^{3}}.6}=\frac{3\sqrt{3}{{.6}^{3}}}{3\sqrt{3}.6}=36.$
Vậy ${{V}_{\max }}=36.$
Nhận
xét: Đối với bài này, học sinh chỉ cần hình dung được
mặt cầu đã cho phải ngoại tiếp hình hộp chữ nhật dựng trên các tia $AB,AC,AD$.
Việc tính toán gần như không có.
Câu
48: Cho hàm số $f\left( x \right)$ thỏa mãn $f\left(
2 \right)=-\frac{2}{9};{f}'\left( x \right)=2x{{\left[ f\left( x \right)
\right]}^{2}}$ với mọi $x\in \mathbb{R}$. Tính $f\left( 1 \right)=?$
LG:
Dễ thấy $\frac{{{f}'}}{{{f}^{2}}}=2x\Rightarrow
-\frac{1}{f}={{x}^{2}}+C;C=-\frac{1}{f\left( 2
\right)}-4=\frac{1}{2}\Rightarrow f\left( 1
\right)=-\frac{1}{{{I}^{2}}+1/2}=-\frac{2}{3}.$
Nhận
xét: Đây là một
bài nguyên hàm đơn giản, việc cho ${f}'$ và ${{f}^{2}}$ ở hai vế gần như
gợi ý luôn hướng giải. Có thể băn khoăn rằng việc chia 2 vế cho ${{f}^{2}}$ có
hợp lệ không. Câu trả lời là có. Vì nếu giả sử tồn tại ${{x}_{0}}$ sao cho $f\left(
{{x}_{0}} \right)=0$. Không mất tổng quát ta xem ${{x}_{0}}>2$ là số nhỏ nhất
có tính chất này, như vậy trên một khoảng dạng $\left( b;{{x}_{0}}
\right),b<2$, thì $f\left( x \right)=-\frac{1}{{{x}^{2}}+C}$ với 1 hằng số $C$
nào đó. Lấy giới hạn của $f\left( x \right)$ khi $x\to {{x}_{0}}$ thì $-\frac{1}{{{x}_{0}}+C}=0$.
Đây là điều vô lý. Tất nhiên là với câu hỏi trắc nghiệm thì học sinh sẽ không
phải băn khoăn về bước này vì khi đã tìm được hàm $f\left( x \right)=-\frac{1}{{{x}^{2}}+C}$
thì đó chắc chắn phải là hàm đầu bài đã cho.
Câu
49: Trong không gian $Oxyz$, cho đường thẳng $d:\left\{
x=1+3t;y=1+4t;z=1 \right\}$. Gọi $\Delta $ là đường thẳng đi qua $A\left( 1;1;1
\right)$ có vector chỉ phương $\vec{u}=\left( 1;-2;2 \right)$. Đường phân giác
của góc nhọn tạo bởi $d$ và $\Delta $ có phương trình là?
LG:
Ta có ${{\vec{u}}_{d}}=\left( \frac{3}{5};\frac{4}{5};0 \right)$. Vì ${{\vec{u}}_{d}}.\vec{u}=-1<0$
nên chọn ${{\vec{u}}_{\Delta }}=-\frac{{\vec{u}}}{\left\| {\vec{u}}
\right\|}=\left( -\frac{1}{3};\frac{2}{3};-\frac{2}{3} \right)$;
${{\vec{u}}_{pg}}={{\vec{u}}_{d}}+{{\vec{u}}_{\Delta
}}=\left( \frac{4}{15};\frac{22}{15};-\frac{10}{15} \right)$. Vậy đường phân
giác là
${d}':\left\{ x=-1+2t;y=-10+11t;x=6-5t \right\}$.
Nhận xét: Bài này có thể gây khó khăn cho thí sinh khi phải lựa chọn giữa phân giác trong và phân giác ngoài của góc. Còn phương pháp chuẩn hóa vector để tìm vector chỉ phương của đường phân giác là khá quen thuộc.
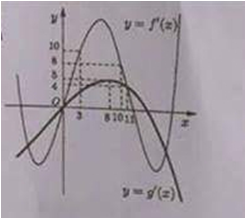
Câu 50: Cho hai hàm số $y=f\left( x \right),y=g\left( x \right)$. Hai hàm số $y={f}'\left( x \right)$ và $y={g}'\left( x \right)$ có đồ thị như hình vẽ bên, trong đó đường cong đậm hơn là đố thị của hàm số $y={g}'\left( x \right)$. Hàm số $h\left( x \right)=f\left( x+4 \right)-g\left( 2x-\frac{3}{2} \right)$ đồng biến trên khoảng nào dưới đây? A. $\left( 5;\frac{31}{5}
\right).$ B. $\left( \frac{9}{4};3
\right)$. C.
$\left( \frac{31}{5};+\infty \right).$ D.
$\left( 6;\frac{25}{4} \right).$
|
|
LG:
Đây là câu duy nhất trong đề thi mà việc sử dụng phương pháp loại trừ đáp án sẽ
tìm ra kết quả nhanh nhất. Ta thấy ${f}'\left( x+4 \right)-2{g}'\left(
2x-\frac{3}{2} \right)$. Như vậy sẽ đưa đến việc so sánh giá trị của ${f}'$ và
2 lần giá trị của ${g}'$. Nếu để ý sẽ thấy các số $10=5.2;8=4.2$. Như vậy nhiều
khả năng để $h$ nghịch biến thì miền giá trị của bên ${f}'$nằm dưới 8, còn miền
giá trị của bên ${g}'$ nằm trên 4. Từ duy luận đó và xét các điểm đặc biệt trên
trục hoành ta thấy ${h}'\left( 6 \right)={f}'\left( 10 \right)-2{g}'\left( 10,5
\right)<8-2.4=0$. Vậy phương án $A,C,D$ đều chứa 1 khoảng xung quanh giá trị
6 mà trên đó $h$ nghịch biến. Vậy đáp án đúng là B.