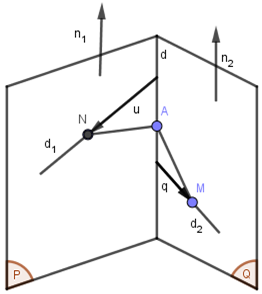
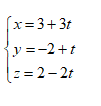Dạng 1: Viết phương trình đường thẳng d
đi qua A và cắt hai đường thẳng ${{d}_{1}};{{d}_{2}}$
cho trước.
Phương pháp giải
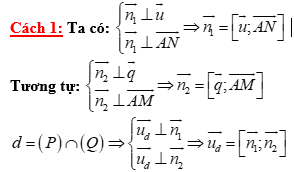
Cách 2: Lập phương trình mặt phẳng (P) ta có: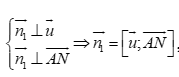 
, (P) đi qua điểm N
Tìm
Khi đó đường thẳng AB chính là đường thẳng d.
Bài 1: Trong hệ tọa độ Oxyz,viết phương trình đường thẳng d đi
qua $A\left( 1;1;0 \right)$ và cắt hai đường thẳng
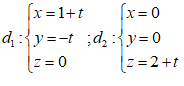( t là tham số)
Hướng dẫn giải
Giả sử d là đường thẳng cần dựng và $d\cap {{d}_{1}}=B;d\cap {{d}_{2}}=C$. Khi đó:
$B\in {{d}_{1}}\Rightarrow B\left( 1;0;0 \right);\,C\in {{d}_{2}}\Rightarrow C\left( 0;0;2 \right)$
$\overrightarrow{{{n}_{{{d}_{1}}}}}=\left[ \overrightarrow{{{u}_{{{d}_{1}}}}};\overrightarrow{AB} \right]=\left[ \left( 1;-1;0 \right);\left( 0;-1;0 \right) \right]=\left( 0;0;-1 \right)$
$\overrightarrow{{{n}_{{{d}_{2}}}}}=\left[ \overrightarrow{{{u}_{{{d}_{2}}}}};\overrightarrow{AC} \right]=\left[ \left( 0;0;1 \right);\left( -1;-1;2 \right) \right]=\left( 1;-1;0 \right)$
Vậy ta chọn $\overrightarrow{{{u}_{d}}}=\left( 1;1;0 \right)$
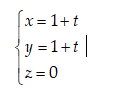
Bài 2: Trong không gian Oxyz, cho điểm $A\left(
1;-1;1 \right)$ và hai đường thẳng $\Delta
:\frac{x-1}{2}=\frac{y}{1}=\frac{z-3}{-1};\Delta
':\frac{x}{1}=\frac{y+1}{-2}=\frac{z-2}{1}$ . Phương trình đường thẳng đi qua
điểm A và cắt hai đường thẳng $\Delta ;\Delta '$ là:
Bài 1:
Đáp án C
Bài 3: Trong không gian Oxyz, cho điểm $A\left( 3;10;1 \right)$ và hai đường thẳng $\Delta :\frac{x-2}{3}=\frac{y+1}{1}=\frac{z+3}{2}$ .và $\Delta ':\frac{x-3}{1}=\frac{y-7}{-2}=\frac{z-1}{-1}$ Phương trình đường thẳng đi qua điểm A và cắt hai đường thẳng $\Delta ;\Delta '$ là:
Đáp án A
Dạng 2: Viết
phương trình đường thẳng d thỏa mãn $d//{{d}_{1}}$ và d cắt ${{d}_{2}};{{d}_{3}}$
Phương pháp giải
Cách 1: Gọi $A\in {{d}_{2}};B\in {{d}_{3}}$ (
ta mã hóa tọa độ)
Khi đó phương trình đường thẳng AB chính là phương trình đường thẳng d sao
cho:
$AB//{{d}_{1}}$ , nghĩa là: $\overrightarrow{AB}=k\overrightarrow{{{u}_{{{d}_{1}}}}}$
Cách 2: Viết phương trình mặt phẳng $\left( P
\right)//{{d}_{1}}$ và chứa ${{d}_{2}}$ ta có: $\overrightarrow{{{n}_{\left( P
\right)}}}=\left[ \overrightarrow{{{u}_{{{d}_{1}}}}};\overrightarrow{{{u}_{{{d}_{2}}}}}
\right]$
Viết phương trình mặt phẳng $\left( Q \right)//{{d}_{1}}$ và chứa ${{d}_{2}}$
có: $\overrightarrow{{{n}_{\left( Q \right)}}}=\left[
\overrightarrow{{{u}_{{{d}_{1}}}}};\overrightarrow{{{u}_{{{d}_{3}}}}} \right]$
Khi đó: $d=\left( P \right)\cap \left( Q \right)$
Bài 1: Trong
không gian với hệ tọa độ Oxyz, viết phương trình đường thẳng d biết d song song
với $d':\frac{x-4}{1}=\frac{y-7}{4}=\frac{z-3}{-2}$ đồng thời cắt cả hai đường thẳng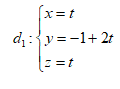 
và đường thẳng ${{d}_{2}}:\frac{x}{1}=\frac{y-1}{-2}=\frac{z-1}{3}$ .
Hướng dẫn giải
Gọi $A\in {{d}_{1}}\Rightarrow A\left(
t;-1+2t;t \right)$; $B\in {{d}_{2}}\Rightarrow B\left( t';1-2t';1+3t' \right)$
Khi đó: $\overrightarrow{AB}\left(
t'-t;2-2t'-2t;1+3t'-t \right)$
Do $d//d'$ nên $\overrightarrow{{{u}_{d'}}}$ và $\overrightarrow{AB}$ cùng phương.
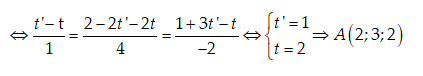
Vậy d là phương trình đường thẳng đi qua A và nhận $\overrightarrow{{{u}_{d'}}}$ là VTCP, vậy d có phương trình là:
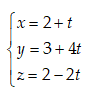
Bài 2: Trong
không gian hệ tọa độ Oxyz đường thẳng $\Delta //{{d}_{1}}$,cắt ${{d}_{2}};{{d}_{3}}$
biết ${{d}_{1}}:\frac{x-1}{2}=\frac{y+1}{1}=\frac{z+2}{-3}$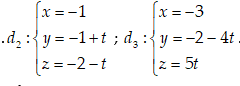 
Đường thẳng nào sau đây không phải là
phương trình đường thẳng ∆
|
A. $\frac{x-1}{-6}=\frac{y+1}{1}=\frac{z-1}{7}$
|
B. $\frac{x+1}{-6}=\frac{y-1}{-1}=\frac{z+1}{7}$
|
|
C. $\frac{x-1}{-6}=\frac{y+1}{-1}=\frac{z-1}{7}$
|
D. $\frac{x-1}{6}=\frac{y+1}{1}=\frac{z-1}{7}$
|
|
A.
$\frac{x+1}{2}=\frac{y+\frac{14}{9}}{1}=\frac{z-\frac{5}{9}}{-3}$
|
B.
$\frac{x+1}{2}=\frac{y-\frac{5}{9}}{1}=\frac{z+\frac{22}{9}}{-3}$
|
|
C.
$\frac{x+3}{-2}=\frac{y+\frac{14}{9}}{-1}=\frac{z-\frac{5}{9}}{3}$
|
D. $\frac{x+3}{2}=\frac{y+\frac{14}{9}}{1}=\frac{z-\frac{5}{9}}{-3}$
|
Dạng 3: Viết phương trình
đường thẳng d đi qua điểm A, vuông góc ${{d}_{1}}$ cắt ${{d}_{2}}$
Phương pháp giải
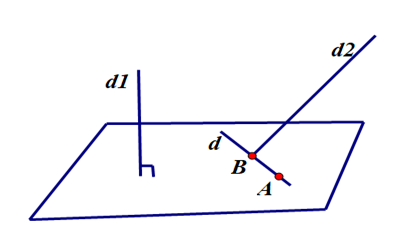
Cách 1: Viết phương trình mặt phẳng $\left( P
\right)$ đi qua A và vuông góc với ${{d}_{1}}$
$\overrightarrow{{{n}_{\left( P \right)}}}=\overrightarrow{{{u}_{{{d}_{1}}}}}$
Tìm $B={{d}_{2}}\cap \left( P \right)$
Khi đó đường thẳng d chính là đường thẳng AB
Cách 2: Lấy $B\in {{d}_{2}}$, khi đó đường thẳng
d chính là đường thẳng AB có $\overrightarrow{{{u}_{d}}}=\overrightarrow{AB}$
Bài 1: Trong
không gian hệ tọa độ Oxyz, viết phương trình đường thẳng d đi qua .., vuông góc
với đường thẳng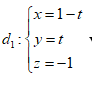 
và cắt
đường thẳng 
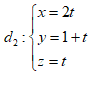( t là
tham số)
Hướng dẫn giải
Giả sử đường thẳng d là đường thẳng cần
dựng và cắt ${{d}_{2}}$ tại B, khi đó: $B\left( 2t;1+t;t \right)$ và:
$\overrightarrow{AB}\left( 2t;t;t-1
\right)$. Gọi $\overrightarrow{{{u}_{1}}}\left( -1;1;0 \right)$ là VTCP của đường
thẳng ${{d}_{1}}$
Vì $d\bot {{d}_{1}}\Leftrightarrow \overrightarrow{AB}.\overrightarrow{{{u}_{1}}}=0\Leftrightarrow t=0\Rightarrow \overrightarrow{AB}\left( 0;0;-1 \right)$
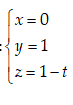( t là tham số).
Bài 2:Trong không gian hệ tọa độ Oxyz, cho điểm $A\left( 1;-1;3
\right)$ và hai đường thẳng ${{d}_{1}}:\frac{x-4}{1}=\frac{y+2}{4}=\frac{z-1}{-2}$
${{d}_{2}}:\frac{x-2}{1}=\frac{y+1}{-1}=\frac{z-1}{1}$ . Viết phương trình
đường thẳng d đi qua điểm A, vuông góc với đường thẳng ${{d}_{1}}$ và cắt đường
thẳng ${{d}_{2}}$
|
A. $\frac{x-1}{4}=\frac{y+1}{1}=\frac{z-3}{4}$
|
B.
$\frac{x-1}{2}=\frac{y+1}{1}=\frac{z-3}{3}$
|
|
C. $\frac{x-1}{2}=\frac{y+1}{-1}=\frac{z-3}{-1}$
|
D.
$\frac{x-1}{-2}=\frac{y+1}{2}=\frac{z-3}{3}$
. |
Đáp án C
Phương pháp giải
Cách 1: Lấy $B\in d'$ ( ta mã hóa tọa độ)
Khi đó đường thẳng d chính là đường
thẳng AB
$\overrightarrow{AB}.\overrightarrow{{{n}_{\left(
Q \right)}}}=0$
Cách 2: Viết
phương trình mặt phẳng $\left( P \right)$ qua điểm A và song song với $\left( Q
\right)$
Khi đó: $B=d'\cap \left( P
\right)$
Do vậy phương trình đường thẳng d chính là phương trình đường thẳng AB
Bài 1: Cho đường thẳng $d:\frac{x-3}{1}=\frac{y-3}{3}=\frac{z}{2}$
, mặt phẳng $\left( Q \right):x+y-z+3=0$ và điểm $A\left( 1;2;-1 \right)$ . Viết
phương trình đường thẳng ∆ đi qua A cắt d và song song với mặt phẳng $\left( Q
\right)$
Hướng dẫn giải
Giả sử ∆ cắt d tại $B\left( 3+t;3+3t;2t \right)$ khi đó: $\overrightarrow{AB}=\left(
2+t;1+3t;2t+1 \right)$
Mặt khác:$AB//\left( Q \right)\Rightarrow 2+t+1+3t-2t-1=0\Leftrightarrow
t=-1$
Suy ra $B\left( 2;0;-2 \right)\Rightarrow \overrightarrow{AB}\left( 1;-2;-1 \right)$ do đó: $AB:\frac{x-1}{2}=\frac{y-2}{-2}=\frac{z+1}{-1}$
Dạng 5: Viết phương trình đường thẳng d nằm
trong mặt phẳng $\left( P \right)$ và cắt hai đường ${{d}_{1}};{{d}_{2}}$
Phương pháp giải
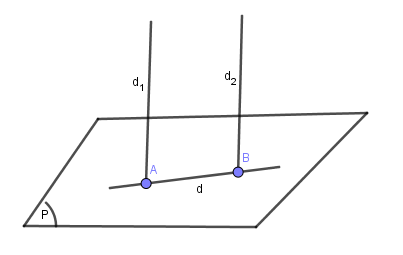
Lấy $A\in {{d}_{1}};B\in {{d}_{2}}$
( ta mã hóa tọa độ các điểm)
Khi đó phương trình đường thẳng d chính là phương trình đường thẳng AB.
$\overrightarrow{AB}.\overrightarrow{{{n}_{\left( P \right)}}}=0$
Bài 1: Trong không gian với hệ tọa độ Oxyz, cho hai đường thẳng ${{d}_{1}}:\frac{x+1}{2}=\frac{y-1}{-1}=\frac{z-1}{2};\,$ ${{d}_{2}}:\frac{x-1}{1}=\frac{y-2}{1}=\frac{z+1}{2}$ và mặt phẳng $\left( P \right):x-y-2z+3=0$. Viết phương trình đường thẳng d nằm trên mặt phẳng $\left( P \right)$ và cắt hai đường thẳng${{d}_{1}};{{d}_{2}}$
Hướng dẫn giải
Ta có: $A={{d}_{1}}\cap \left( P \right)\Rightarrow A\left( -1+2t;1-t;1+t
\right);B={{d}_{2}}\cap \left( P \right)\Rightarrow B\left( 1+t';2+t';-1+2t'
\right)$
Mặt khác có: $A\in \left( P \right)\Rightarrow -1+2t-\left( 1-t
\right)-2\left( 1+t \right)+3=0\Leftrightarrow t=1\Rightarrow A\left( 1;0;2
\right)$
Tương tự: $B\in \left( P \right)\Rightarrow B\left( 2;3;1 \right)$
Vì A, B thuộc $\left( P \right)$ nên đường thẳng d đi qua A,B và nằm trong $\left(
P \right)$
Ta có: $\overrightarrow{{{u}_{d}}}=\overrightarrow{AB}=\left( 1;3;-1
\right)$
Vậy phương trình đường thẳng d cần tìm là:
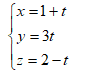
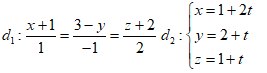và mặt phẳng $\left( P \right):x-2y+z-2=0$. Viết
phương trình đường thẳng d nằm trên mặt phẳng $\left( P \right)$ và cắt hai đường
thẳng ${{d}_{1}};{{d}_{2}}$
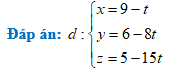
Dạng 6: Viết
phương trình đường thẳng d nằm trong mặt phẳng $\left( P \right)$ và vuông góc
với d’ cho trước tại giao điểm $I=d'\cap \left( P \right)$
Phương pháp giải
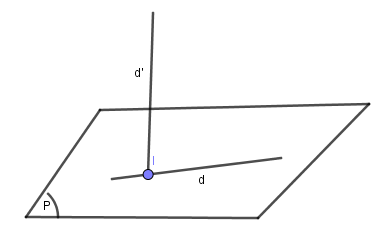
Tìm $I=d'\cap \left( P \right)$
Khi đó: $\overrightarrow{{{u}_{d}}}=\left[ \overrightarrow{{{u}_{d'}}};\overrightarrow{{{n}_{\left( P \right)}}} \right]$
Bài 1: Trong không gian hệ tọa Oxyz, cho đường thẳng $d:\frac{x+2}{1}=\frac{y-2}{1}=\frac{z}{-1}$
và mặt phẳng $\left( P \right):x+2y-3z+4=0$. Viết phương trình đường thẳng ∆ nằm
trong (P) sao cho ∆ vuông góc với d tại giao điểm của d với (P).
Hướng dẫn giải
Gọi $A=d\cap \left( P \right)\Rightarrow A\left( -3;1;1
\right);\overrightarrow{{{u}_{\Delta }}}\left( 1;1;-1
\right);\overrightarrow{{{n}_{\left( P \right)}}}=\left( 1;2;-3 \right)$
Đường thẳng ∆ đi qua A và có VTCP $\overrightarrow{{{u}_{d}}}=\left[ \overrightarrow{{{u}_{\Delta }}};\overrightarrow{{{n}_{\left( P \right)}}} \right]=\left( -1;2;1 \right)$ nên có phương trình $\frac{x+3}{-1}=\frac{y-1}{2}=\frac{z-1}{1}$
Dạng 7: Viết
phương trình đường vuông góc chung của hai đường thẳng chéo nhau.
Phương pháp giải
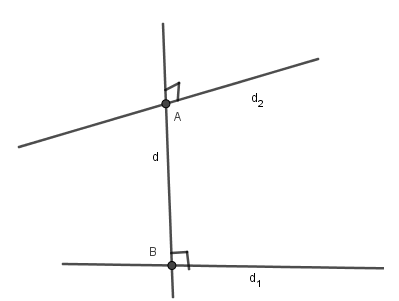
Cách 1: Ta
có: $\overrightarrow{{{u}_{d}}}=\left[
\overrightarrow{{{u}_{1}}};\overrightarrow{{{u}_{2}}} \right]$
Viết phương trình mặt phẳng $\left(
P \right)$ chứa ${{d}_{1}}$ $\overrightarrow{{{n}_{1}}}=\left[
\overrightarrow{{{u}_{d}}};\overrightarrow{{{u}_{1}}} \right]$
Viết phương trình mặt phẳng $\left(
Q \right)$ chứa ${{d}_{2}}$ $\overrightarrow{{{n}_{2}}}=\left[
\overrightarrow{{{u}_{d}}};\overrightarrow{{{n}_{2}}} \right]$
Khi đó: $d=\left( P \right)\cap
\left( Q \right)$
Cách 2: Lấy $A\in {{d}_{1}};B\in {{d}_{2}}$ ( ta mã hóa tọa độ)
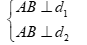
Bài 1: Trong không gian hệ tọa độ Oxyz, cho hai đường thẳng ${{\Delta
}_{1}}:\frac{x+1}{2}=\frac{y+2}{1}=\frac{z-1}{1}$ và đường thẳng ${{\Delta
}_{2}}:\frac{x+2}{-4}=\frac{y-1}{1}=\frac{z+2}{-1}$. Tìm đường vuông góc chung
của ${{\Delta }_{1}};{{\Delta }_{2}}$
Hướng dẫn giải
${{\Delta }_{1}}$
có VTCP: $\overrightarrow{{{u}_{1}}}\left( 2;1;1 \right)$
${{\Delta }_{2}}$
có VTCP: $\overrightarrow{{{u}_{2}}}\left( -4;1;-1 \right)$
Gọi Δ là đường vuông góc chung.
Giao điểm của Δ với ${{\Delta
}_{1}}$ và ${{\Delta }_{2}}$ lần lượt là A,B
Suy ra: Tọa độ của $A\left(
2a-1;a-2;a+1 \right);B\left( -4b-2;b+1;-b-2 \right)$
$\overrightarrow{AB}\left(
2a+4b+1;a-b-3;a+b+3 \right)$
Đường thẳng vuông góc chung sẽ đi qua AB suy ra AB vuông góc với ${{\Delta }_{1}}$ và ${{\Delta }_{2}}$
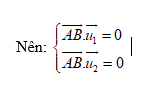
Giải phương trình ta được
$a=1;b=-1$
Suy ra: $A\left( 1;-1;2
\right);B\left( 2;0;-1 \right)$
Phương trình đường vuông góc chung là:
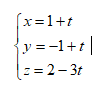
Bài 2: Trong không gian hệ tọa độ Oxyz, cho hai đường thẳng ${{\Delta
}_{1}}:\frac{x-1}{1}=\frac{y}{2}=\frac{z-1}{1}$ và đường thẳng ${{\Delta
}_{2}}:\frac{x-1}{2}=\frac{y-1}{1}=\frac{z}{1}$. Tìm đường vuông góc chung của ${{\Delta
}_{1}};{{\Delta }_{2}}$
Dạng 8:Viết
phương trình đường thẳng d vuông góc với mặt phẳng $\left( P \right)$ và cắt
hai đường thẳng ${{d}_{1}};{{d}_{2}}$
Phương pháp giải
Cách 1: Viết
phương trình mặt phẳng $\left( P' \right)$ chứa ${{d}_{1}}\bot \left( P
\right)$ $\Rightarrow \overrightarrow{{{n}_{\left( P' \right)}}}=\left[
\overrightarrow{{{u}_{{{d}_{1}}}}};\overrightarrow{{{n}_{\left( P \right)}}}
\right]$
Viết phương trình mặt phẳng $\left(
Q \right)$ chứa ${{d}_{2}}\bot \left( P \right)\Rightarrow
\overrightarrow{{{n}_{\left( Q \right)}}}=\left[
\overrightarrow{{{u}_{{{d}_{2}}}}};\overrightarrow{{{n}_{\left( P \right)}}}
\right]$
Khi đó: $d=\left( P' \right)\cap
\left( Q \right)$
Cách 2:
Lấy $A\in {{d}_{1}};B\in {{d}_{2}}$ mã hóa tọa độ
Khi đó phương trình đường thẳng d
cính là phương trình đường thẳng AB
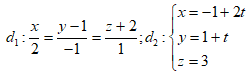( t là tham số). Viết phương trình đường thẳng vuông góc với mặt phẳng $\left(
P \right):7x+y-4z=0$ và cắt cả hai đường thẳng ${{d}_{1}};{{d}_{2}}$.
Hướng dẫn giải
Giả sử $d\cap {{d}_{1}}=A\Rightarrow A\in {{d}_{1}}\Rightarrow A\left(
2t;1-t;t-2 \right)$
Tương tự: $d\cap {{d}_{2}}=B\Rightarrow B\in {{d}_{2}}\Rightarrow B\left(
2u-1;u+1;3 \right)$
Vì thế: $\overrightarrow{AB}\left( 2u-2t-1;u+t;5-t \right)$ là VTCP của d
Do $d\bot \left( P \right)\Rightarrow
\overrightarrow{AB}//\overrightarrow{{{n}_{\left( P \right)}}}\left( 7;1;-4
\right)$
Từ đó ta có hệ phương
trình: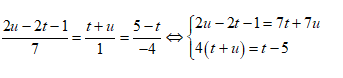 
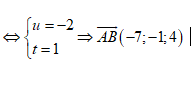
Vậy phương trình đường thẳng d đi qua điểm $A\left( 2;0;-1 \right)$ nên $d:\frac{x-2}{7}=\frac{y}{1}=\frac{z+1}{-4}$
Bài 2: Trong không gian với hệ trục tọa độ Oxyz, cho hai đường thẳng ${{d}_{1}};{{d}_{2}}$ có phương trình lần lượt là: ${{d}_{1}}:\frac{x-1}{2}=\frac{y+1}{1}=\frac{z-2}{-1};{{d}_{2}}:\frac{x-2}{1}=\frac{y}{-1}=\frac{z+2}{3}$ ( t là tham số). Viết phương trình đường thẳng vuông góc với mặt phẳng $\left( P \right):x+2y-z+1=0$ và cắt cả hai đường thẳng ${{d}_{1}};{{d}_{2}}$.
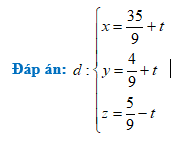
Dạng 10: Viết phương trình
đường thẳng d đi qua điểm A, vuông góc với đường thẳng ${{d}_{1}}$ và cắt đường thẳng ${{d}_{1}}$
Phương pháp giải
Gọi H là hình chiều vuông góc của
A lên ${{d}_{1}}$ do đó ta mã hóa tọa độ H
Do $AH\bot
{{d}_{1}}\Leftrightarrow \overrightarrow{AH}.\overrightarrow{{{u}_{1}}}=0$
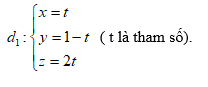
Hướng dẫn giải
Gọi H là hình chiếu của A lên ${{d}_{1}}$ do đó: $H\left( t;1-t;2t
\right)\Rightarrow \overrightarrow{AH}\left( t-1;-t-1;2t+2 \right)$
$\overrightarrow{{{u}_{1}}}\left( 1;-1;2 \right)$ là VTCP của ${{d}_{1}}$
Do $AH\bot {{d}_{1}}\Leftrightarrow
\overrightarrow{AH}.\overrightarrow{{{u}_{1}}}=0\Leftrightarrow
6t+4=0\Rightarrow t=-\frac{3}{2}\Rightarrow \overrightarrow{AH}\left(
-\frac{5}{3};-\frac{1}{3};\frac{2}{3} \right)$
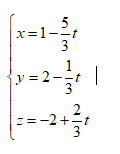
Bài 2: Trong không gian tọa độ Oxyz, viết phương trình đường thẳng d đi qua điểm $A\left( -4;-2;4 \right)$ và vuông góc với đường thẳng ${{d}_{1}}:\frac{x+3}{2}=\frac{y-1}{-1}=\frac{z+1}{4}$.
|
A. $\frac{x+4}{-4}=\frac{y+2}{-4}=\frac{z-4}{1}$
|
B.
$\frac{x+4}{-1}=\frac{y+2}{2}=\frac{z-4}{1}$ |
|
C. $\frac{x+4}{2}=\frac{y+2}{-2}=\frac{z-4}{-1}$ |
D.
$\frac{x+4}{3}=\frac{y+2}{2}=\frac{z-4}{-1}$ |
Đáp án D
Dạng 11: Viết phương trình tham số của đường thẳng d là hình chiếu của $d'$ trên mặt phẳng $\overrightarrow{u}$ .
Phương pháp giải
Xác
định điểm chung của $d'$ và mặt phẳng $\left(
P \right)$
+Nếu
$d'\subset \left( P \right)$ thì hình
chiếu của $d'$chính là $d'$
+Nếu
$d'//\left( P \right)$ thì:
*Xác định $A\in d'$
*Xác
định B là hình chiếu vuông góc của A trên $\left( P \right)$
*d
là đường thẳng đi qua B và $//d'$
+Nếu
$d'\cap \left( P \right)=M$ thì:
*Xác
định $A\in d'$ (A không trùng với M)
*Xác
định B là hình chiếu vuông góc của A trên $\left( P \right)$
Bài 1: Trong không gian với hệ
toạ độ Oxyz, viết phương trình tham số của đường thẳng d là hình chiếu của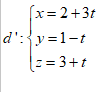 
trên mặt phẳng $\left( P \right):2x-3y+z+1=0$
Hướng dẫn giải
Gọi $M=d'\cap \left( P \right)\Rightarrow M\left(
\frac{1}{2};\frac{3}{2};\frac{5}{2} \right)$
Ta có: $A\left( 2;1;3 \right)\in d'$
Gọi ${{d}_{1}}$ là đường thẳng đi qua A và vuông góc với $\left( P \right)$
nên có phương trình là: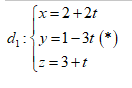
Gọi B là hình chiếu vuông góc của A trên $\left( P \right)\Rightarrow
B=\left( P \right)\cap {{d}_{1}}$
Thay (*) và phương trình mặt phẳng $\left( P \right)$ ta được: $2\left(
2t+2 \right)-3\left( 1-3t \right)+3+t+1=0$
$\Leftrightarrow t=-\frac{5}{14}\Rightarrow B\left(
\frac{9}{7};\frac{29}{14};\frac{37}{14} \right)\Rightarrow
\overrightarrow{MB}\left( \frac{11}{14};\frac{8}{14};\frac{2}{14} \right)$
Đường thẳng d cần tìm là đường thẳng đi qua C và nhận $\overrightarrow{u}\left( 11;8;2 \right)$ là VTCP
Vậy phương trình d là: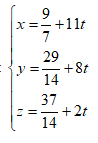 
Bài 2: Trong không gian với hệ toạ độ Oxyz, viết phương trình tham số của đường thẳng d là hình chiếu của $d':\frac{x-1}{2}=\frac{y+1}{1}=\frac{z-2}{1}$ trên mặt phẳng $\left( Oxy \right)$
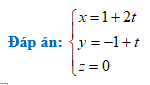
Dạng 12: Viết phương trình
đường thẳng d song song và cách đều hai đường thẳng song song ${{d}_{1}}$ và ${{d}_{2}}$ đồng thời d
nằm trong mặt phẳng chứa ${{d}_{1}}$ và ${{d}_{2}}$
Phương pháp giải
- VTCP $\overrightarrow{u}$ của d là VTCP
của ${{d}_{1}}$ hoặc ${{d}_{2}}$
- Xác định toạ độ điểm $M\in
{{d}_{1}};N\in {{d}_{2}}$ toạ độ trung
điểm I của MN thuộc d.
- Vậy đường thẳng d cần tìm là đường thẳng đi qua I và nhận $\overrightarrow{u}$ là VTCP
Bài 1: Trong không gian với hệ
toạ độ Oxyz, cho hai đường thẳng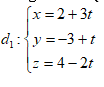 
( t là tham số ) và ${{d}_{2}}:\frac{x-4}{3}=\frac{y+1}{1}=\frac{z}{-2}$
. Viết phương trình tham số của đường thẳng d nằm trong mặt phẳng chứa ${{d}_{1}}$
và ${{d}_{2}}$ đồng thời cách đều hai đường
thẳng đó.
Hướng dẫn giải
Do ${{d}_{1}}//{{d}_{2}}$ và d cách
đều ${{d}_{1}};{{d}_{2}}$ chỉ phương của d là $\overrightarrow{u}\left( 3;1;-2
\right)$
Lấy $M\left( 2;-3;4 \right)\in {{d}_{1}};N\left( 4;-1;0 \right)\in {{d}_{2}}$ toạ độ trung điểm I của MN là $I\left( 3;-2;2 \right)\in d$
Phương trình tham số của d là 
