Công thức giải nhanh các dạng toán Max - Min Số Phức

Bài 1: Tìm giá trị nhỏ nhất của $\left| z \right|$,biết rằng số phức z thỏa mãn điều kiện $\left| z-1+i \right|=1$

Hướng dẫn giải:

Đáp án C

Khi đó có: $x=-1;y=1;k=1$

Vậy giá trị nhỏ nhất của $\left| z \right|=\left| 1-\sqrt{{{1}^{2}}+{{1}^{2}}} \right|=\sqrt{2}-1$

Bài 2: Cho số phức z thỏa mãn $\left| z-2+2i \right|=1$ . Tìm giá trị lớn nhất ,nhỏ nhất  lần lượt của $\left| z \right|$

Bài 3: Tìm số phức z sao cho $\left| z-3i+1 \right|$ đạt giá trị nhỏ nhất?

Bài 4: Trong các số phức z thỏa mãn $\left| z-3+4i \right|=5$, gọi ${{z}_{0}}$ là số phức có modun lớn nhất. Tổng phần thức và phần ảo của ${{z}_{0}}$bằng:

Bài 5: Trong các số phức z thỏa mãn $\left| z-1+2i \right|\le 2\sqrt{5}$, gọi M, m lần lượt là GTLN,GTNN của $\left| z \right|$ . Tính $M+m$

Bài 1:  Cho số phức z thỏa mãn $\left| \frac{3-3\sqrt{2}i}{1+2\sqrt{2}i}z-1-\sqrt{2}i \right|=\sqrt{3}$ . Gọi M và m lần lượt là giá trị lớn nhất và nhỏ nhất của biểu thức $P=\left| z-3-3i \right|$ . Tính Mm.

Chọn C

Áp dụng công thức trên với ${{z}_{1}}=\frac{3-3\sqrt{2}i}{1+2\sqrt{2}i};{{z}_{2}}=1+\sqrt{2}i;{{z}_{3}}=3+3i;r=\sqrt{3}$ ta được: Max=6; min=4

Khi đó Mm=24

Bài 2: Tìm giá trị lớn nhất của $\left| z \right|$, biết rằng số phức z thỏa mãn điều kiện: $\left| \frac{-2-3i}{3-2i}z+1 \right|=1$

Bài 3: Cho số phức z thỏa mãn $\left| \frac{1+i}{1-i}z+2 \right|=1$, đặt $m=\min \left| z \right|$ ; M=max$\left| z \right|$ , tìm $\left| m+iM \right|$

Bài 4: Trong các số phức z thỏa mãn điều kiện $\left| z-3-2i \right|=\sqrt{2}$, số phức z có modun nhỏ nhất là:

Bài 5: Tìm GTNN của $\left| z \right|$ biết z thỏa mãn $\left| \frac{4+2i}{1-i}z-1 \right|=1$

Bài 6: ( Chuyên KHTN – L1) Trong các số phức z thỏa mãn điều kiện $\left| \left( 1+i \right)z+1-7i \right|=\sqrt{2}$ . Tìm $\max \left| z \right|$

Bài 1:  Cho số phức z thỏa mãn $\left| z+1 \right|+\left| z-1 \right|=4$ . Gọi m=min$\left| z \right|$ và M=max$\left| z \right|$. Khi đó M.m bằng

Hướng dẫn giải

Chọn B

Áp dụng công thức: với ${{z}_{1}}=1;{{z}_{2}}=1;K=4$

m=min=$\sqrt{3}$ ; M=max =2

Khi đó M.m=$2\sqrt{3}$

Bài 2:  Cho số phức z thỏa mãn $\left| iz+\frac{2}{1-i} \right|+\left| iz-\frac{2}{1-i} \right|=4$ . Gọi m=min$\left| z \right|$ và M=max$\left| z \right|$. Khi đó M.m bằng

Bài 3: Cho số phức z thỏa mãn điều kiện $\left| z+4 \right|+\left| z-4 \right|=10$. Gọi M,m lần lượt là giá trị lớn nhất và nhỏ nhất của \[\left| z \right|\] .Tìm $v=\left| \left( m-4i \right)+\left( 2+Mi \right) \right|$

 Bài 4: (THPT Trần Phú- Hà Nội 2017) Cho số phức z thỏa mãn $\left| z+3 \right|+\left| z-3 \right|=10$. Giá trị nhỏ nhất của $\left| z \right|$ là:

Bài 5: (THPT Thăng Long- Hà Nội 2017 L2) Cho z là số phức thay đổi thỏa mãn $\left| z-2 \right|+\left| z+2 \right|=4\sqrt{2}$. Trong mặt phẳng tọa độ, gọi M,N là điểm biểu diễn của z và $\overline{z}$. Tính giá trị lớn nhất của diện tích tam giác OMN.

Bài 1: (THPT Chuyên Lào Cai 2017 L2) Cho số phức z thỏa mãn $\left| z+\frac{4i}{z} \right|=2$. Gọi M, m lần lượt là giá trị lớn nhất và nhỏ nhất của $\left| z \right|$ . Tính $M+m$ ?

Hướng dẫn giải

Chọn B

Áp dụng công thức ta có: ${{z}_{0}}=4i;K=2$

Ta tính  được: $-1+\sqrt{5}\le \left| z \right|\le 1+\sqrt{5}$

Vậy $M=1+\sqrt{5};m=-1+\sqrt{5}$

Bài 2: Cho số phức z thỏa mãn $\left| \left( 1+i \right){{z}^{2}}+1-2i \right|\le \sqrt{2}\left| z \right|$ . Tìm GTLN,GTNN của $T=\left| z \right|$ 

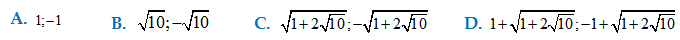
Đáp án :D

Bài 1: Cho số phức z thỏa mãn $\left| z-2 \right|+\left| z+2 \right|=6$ . Tìm GTLN,GTNN của $P=\left| z-1+3i \right|$

Hướng dẫn giải:

Có $a=3;c=2\Rightarrow {{b}^{2}}=5$

Phương trinh chính tắc của elip $\frac{{{x}^{2}}}{9}+\frac{{{y}^{2}}}{5}=1\Rightarrow y=\pm \frac{\sqrt{5}}{3}\sqrt{9-{{x}^{2}}}$

Vậy ${{P}^{2}}={{\left( x-1 \right)}^{2}}+{{\left( \pm \frac{\sqrt{5}}{3}\sqrt{9-{{x}^{2}}} \right)}^{2}}={{f}_{1,2}}\left( x \right)$

Bấm TABLE của hàm ${{f}_{1,2}}\left( x \right)$ với $x\in \left[ -3;3 \right]$ được GTLN,GTNN của ${{P}^{2}}$

Bài 1: Cho số phức z thỏa mãn $\left| z-1+3i \right|+\left| z+2-i \right|=8$. Tìm GTLN,GTNN của $P=\left| 2z+1+2i \right|$

Hướng dẫn giải

Ta có: $P=\left| 2z+1+2i \right|\Rightarrow \frac{P}{2}=\left| z+\frac{1}{2}+i \right|$. Đặt $A=\left| z+\frac{1}{2}+i \right|$

Ta thấy ${{z}_{1}}=1-3i;{{z}_{2}}=-2+i;{{z}_{0}}=-\frac{1}{2}-i$ . Do ${{z}_{0}}=\frac{{{z}_{1}}+{{z}_{2}}}{2}$

Tính $c=\frac{5}{2};a=4\Rightarrow b=\frac{\sqrt{39}}{2}$

Vậy $\max A=4;\min A=\frac{\sqrt{39}}{2}\Rightarrow \max P=8;\min P=\sqrt{39}$

Bài 1: Cho số phức z thỏa mãn $\left| z+1+i \right|=\left| \overline{z}-2i \right|$ .Tìm GTNN của $\left| z \right|$

Hướng dẫn giải

Chọn D

Gọi  $z=x+yi$ thì $M\left( x;y \right)$ là điểm biểu diễn của z. Từ giả thiết có:$\left| z+1+i \right|=\left| \overline{z}-2i \right|\Leftrightarrow {{\left( x+1 \right)}^{2}}+{{\left( y+1 \right)}^{2}}={{x}^{2}}+{{\left( y+2 \right)}^{2}}\Leftrightarrow x-y-1=0\left( d \right)$. Vậy M di chuyển trên (d). Có:

$\left| z \right|=OM$ do đó: $d\left( O;d \right)=\frac{1}{\sqrt{2}}$

Bài 2: Cho số phức z thỏa mãn $\left( z+3-i \right)\left( \overline{z}+1+3i \right)$ là một số thực. Tìm giá trị nhỏ nhất của $T=\left| z-1+i \right|$

Bài 3: Tìm số phức z có $\left| z \right|$ nhỏ nhất , biết rằng số phức z thỏa mãn $\left| z+2 \right|=\left| i-z \right|$

Bài 4: Cho số phức z thỏa mãn điều kiện $v=\left( z-i \right)\left( 2+i \right)$ là một số thuần ảo . Tìm giá trị nhỏ nhất của $\left| z-2+3i \right|$

Bài 5: Trong các số phức z thỏa mãn $\left| z \right|=\left| \overline{z}-3+4i \right|$ , số phức có modun nhỏ nhất là:

Bài 6: Trong các số phức z thỏa mãn điều kiện $\left| z-2-4i \right|=\left| z-2i \right|$. Tìm số phức có modun bé nhất

Bài 7: Cho các số phức z,w thỏa mãn $\left| z+3-2i \right|=\left| \overline{z}+3i \right|,\text{w}=\left( 1+i \right)z+3$ . Giá trị nhỏ nhất của $\left| \text{w} \right|$ là:

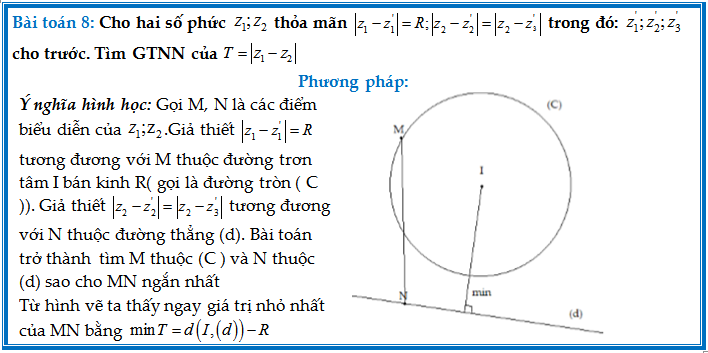
Bài 1: Cho hai số phức ${{z}_{1}};{{z}_{2}}$ thỏa mãn $\left| {{z}_{1}}+5 \right|=5$ và $\left| {{z}_{2}}+1-3i \right|=\left| {{z}_{2}}-3-6i \right|$. Tìm giá trị nhỏ nhất của $T=\left| {{z}_{1}}-{{z}_{2}} \right|$

Hướng dẫn giải

Chọn C

Gọi M,N là các điểm biểu diễn ${{z}_{1}};{{z}_{2}}$. Giả thiết $\left| {{z}_{1}}+5 \right|=5$ tương đương M thuộc đường tròn tâm $I\left( -5;0 \right)$  bán kinh $R=5$ . Giả thiết $\left| {{z}_{2}}+1-3i \right|=\left| {{z}_{2}}-3-6i \right|$ tương đương N thuộc đường tròn thẳng $\left( d \right):8x+6y-35=0$. Vậy $\min MN=d\left( I,\left( d \right) \right)-R=\frac{15}{2}-5=\frac{5}{2}$

Bài 2: Cho hai số phức ${{z}_{1}};{{z}_{2}}$ thỏa mãn $\left| {{z}_{1}}+4-3i \right|=2$ và $\left| {{z}_{2}}+2-3i \right|=\left| {{z}_{2}}-1+2i \right|$. Tìm giá trị nhỏ nhất của

$T=\left| {{z}_{1}}-{{z}_{2}} \right|$

Đáp án A

Bài 1: Cho số phức z thỏa mãn $\left| z-1 \right|=\sqrt{2}$. Tìm GTLN của $T=\left| z+1 \right|+\left| z-2-i \right|$

Hướng dẫn giải

Chọn A

Áp dụng công thức:

Với ${{z}_{0}}=1;{{z}_{1}}=-i;{{z}_{2}}=2+i;k=1;R=\sqrt{2}$

$T\le 4$

Vậy Max $T=4$

Bài 2: Cho số phức z thỏa mãn $\left| z-1-2i \right|=2$. Tìm Max của $T=\left| z \right|+\left| z-3-6i \right|$

Đáp án B

Bài viết gợi ý: