Câu 1: Cho hàm số $f\left( x \right)$ liên tục trên $\mathbb{R}$
và có $\int\limits_{0}^{1}{f\left( x \right)d\text{x}}=2;\int\limits_{0}^{3}{f\left(
x \right)d\text{x}}=6$.Tính$I=\int\limits_{-1}^{1}{f\left( \left| 2\text{x}-1
\right| \right)d\text{x}}$
A.
$I=\frac{2}{3}$ B.
$I=4$ C. $I=\frac{3}{2}$ D.
$I=6$
Hướng dẫn : Bikiptheluc.com – Loga.vn
Chọn hàm 2 ẩn \[f(x)=ax+b\]
do ta có 2 phương trình
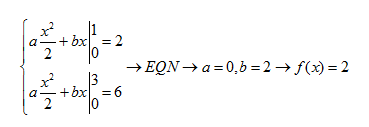
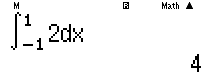
Câu
2: Cho hàm số $y=f(x)$ xác định và liên tục
trên $\mathbb{R}$ có $f(x)>0\text{ }\forall x\in \mathbb{R}$, $f(0)=1$
Biết $\frac{f'(x)}{f(x)}=2-2x$, tìm tất cả các giá trị của m để phương trình $f(x)=m$
có 2 nghiệm thực phân biệt.
A.
$1<><> B. $0<><> C. $m>e$ D. $0
Hướng dẫn
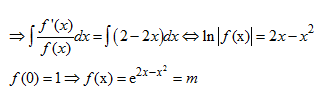
Sau đó các em xét các giá trị m đặc trưng ở các đáp án, hoặc khảo sát
bằng Table
Câu 3: Cho biết\[\int\limits_{0}^{4}{\frac{\sqrt{2x+1}}{1+\sqrt{2x+1}}dx}=a+b\ln
2,\,\left( a,b\in \mathbb{Q} \right)\]. Khi đó đẳng thức nào sau đây đúng?
A. $a-b=0$ B.
${{a}^{2}}-4b-1=0$ C. ${{a}^{2}}-4b+1=0$ D. ${{a}^{2}}-4b=0$
Hướng dẫn Bikiptheluc.com – Loga.vn
Các em dùng Table dò được : a=2,b=1
Câu 4. Cho $\int\limits_{0}^{1}{x.\ln
\sqrt{3{{x}^{2}}+1}}dx=a.ln2-\frac{b}{c}$ (với a là số hữu tỉ , b và c là các số
nguyên dương ,$\frac{b}{c}$ là phân số tối giản). Hãy tính giá trị của $a.b.c$
.
A. 6. B. 3. C. $\frac{8}{3}$ D. $\frac{4}{3}$.
Hướng dẫn :
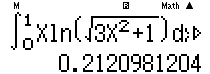
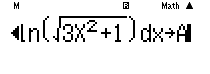
Rút $\frac{b}{c}=A-a\ln 2$ rồi tiến hành dò
Các em dò Table với $F(x)=A-Xln2$
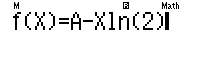
Start $-3=$ End $3=$ Step $\frac{1}{3}=$
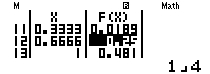
Vậy $a=\frac{2}{3},b=1,c=4\to abc=\frac{8}{3}$
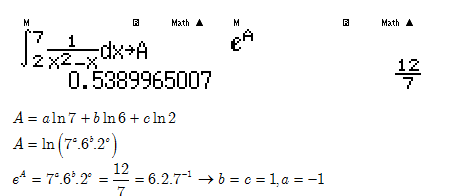
Câu 5: Biết $\int\limits_{2}^{7}{\frac{d\text{x}}{{{x}^{2}}-x}}=a\ln
7+b\ln 6+c\ln 2$, với $a,b,c$ là các số
nguyên. Tính $S=a+2b+c$.
A.
\[\text{S}=3\]. B.
\[\text{S}=4\]. C. $S=2$. D. $S=1$.
Hướng dẫn Bikiptheluc.com – Loga.vn
Câu 6: Cho hàm số $y=f\left( x \right)$ thỏa mãn $f'\left( x
\right).f\left( x \right)={{x}^{4}}+{{x}^{2}}$. Biết $f\left( 0 \right)=2$.
Tính ${{f}^{2}}\left( 2 \right).$
A. ${{f}^{2}}\left( 2
\right)=\frac{313}{15}$. B. ${{f}^{2}}\left( 2
\right)=\frac{332}{15}$. C. ${{f}^{2}}\left( 2 \right)=\frac{324}{15}$. D. \[{{f}^{2}}\left( 2
\right)=\frac{323}{15}\].
Hướng dẫn
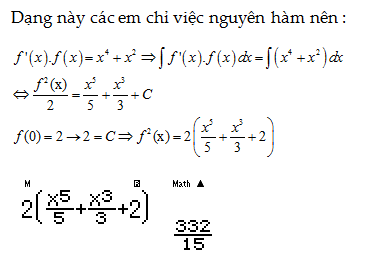
Câu 7: Cho hàm số \[y=f\left( x \right)\] xác định trên \[\mathbb{R}\],
thỏa mãn \[f\left( x \right)>0,\text{ }\forall x\in \mathbb{R}\] và \[f'\left(
x \right)+2f\left( x \right)=0\]. Tính \[f\left( -1 \right)\], biết rằng \[f\left(
1 \right)=1\].
A.
\[3\]. B. \[{{e}^{-2}}\]. C. \[{{e}^{4}}\]. D. \[{{e}^{3}}\].
Hướng
dẫn Bikiptheluc.com – Loga.vn
Các em biến đổi rồi nguyên hàm 2 vế
\[f'\left( x \right)=-2f\left( x \right)\Leftrightarrow \frac{f'\left(
x \right)}{f\left( x \right)}=-2\]
\[\Rightarrow \int{\frac{f'\left( x \right)}{f\left( x
\right)}dx=-2x+C}\]
\[f(1)=1\Rightarrow \ln \left| f(x) \right|=-2x+2\Leftrightarrow
f(x)={{e}^{-2x+2}}\]







