Nếu em nào đã học khóa LiveStream cơ bản và nâng cao của anh tại đây thì sẽ rất dễ dàng kiếm 8 điểm đề này còn chịu khó học thì sẽ tầm 8.5 vì toàn những dạng anh đã dạy kĩ từ cách làm tay tới cách casio để giải nhanh nên các em không có gì bỡ ngỡ cả, ngoài ra sắp tới anh cũng ra mắt cuốn casio ver 3 năm 2018 để giải nhanh dạng 7+ 8+ 9+ như thế này ( tầm 20/5). Thôi mình vào giải nhé
Câu
26. Tìm tất cả các giá trị của tham số m để
phương trình ${{4}^{x}}+{{2}^{x}}+4={{3}^{m}}({{2}^{x}}+1)$ có 2 nghiệm phân biệt
A.${{\log
}_{4}}3\le m<1$ B. ${{\log
}_{4}}3
Hướng
dẫn
Cách
1: Các em xét các đáp án xem đáp án nào làm hàm đổi dấu 2 lần
Cách
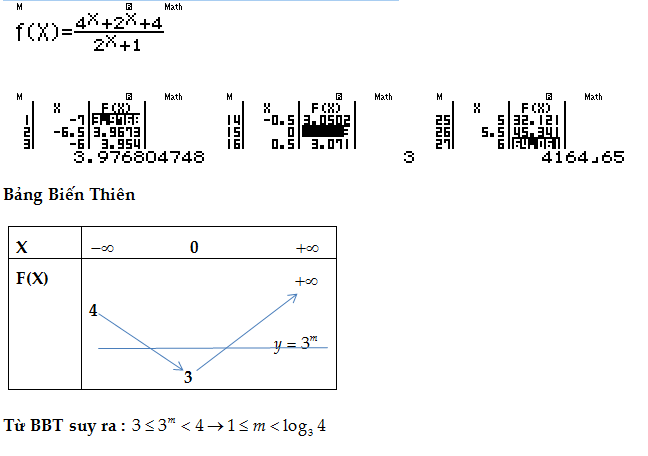
2: Cô lập m xét hàm
${{4}^{x}}+{{2}^{x}}+4={{3}^{m}}({{2}^{x}}+1)\Leftrightarrow {{3}^{m}}=\frac{{{4}^{x}}+{{2}^{x}}+4}{{{2}^{x}}+1}$
Câu
28. Cho $y=f(x)$ là hàm số chẵn và liên tục trên
R. Biết $\int\limits_{0}^{1}{f(x)dx=\frac{1}{2}}\int\limits_{1}^{2}{f(x)dx=1}$ .
Giá trị của $\int\limits_{-2}^{2}{\frac{f(x)}{{{3}^{x}}+1}dx}$ bằng ?
A.3 B.1
C.4 D.6
Hướng
dẫn
Chọn $f(x)=a{{x}^{2}}+b$ là 1 hàm chẵn có 2 biến do mình có 2 điều kiện
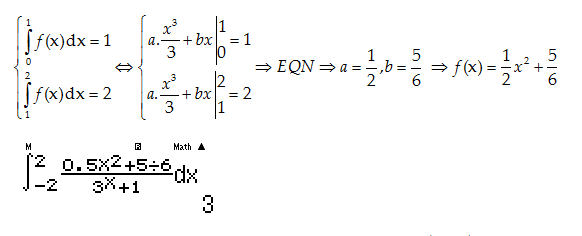
Câu
31. Giả sử $F(x)$ là một nguyên hàm của $f(x)=\frac{\ln
\left( x+3 \right)}{{{x}^{2}}}$ sao cho $F(-2)+F(1)=0$. Giá trị của $F(-1)+F(2)$
bằng
A.$\frac{7}{3}\ln 2$ B.$\frac{2}{3}\ln 2+\frac{3}{6}\ln 5$ C. $\frac{10}{3}\ln 2-\frac{5}{6}\ln 5$ D. $0$
Hướng
dẫn
Các em phải chia làm 2 khoảng do nó bị gián
đoạn tại$x=0$
$-\infty
\to 0:F(-1)=\int\limits_{-2}^{-1}{f(x)dx}+F(-2)$
$0\to +\infty :F(2)=\int\limits_{1}^{2}{f(x)dx}+F(1)$
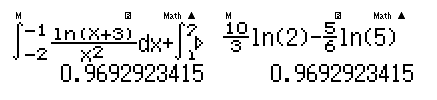
Câu
39. Biết rằng giá trị nhỏ nhất của hàm số $y=mx+\frac{36}{x+1}$
trên $\left[ 0;3 \right]$ bằng 20. Mệnh
đề nào sau đây đúng ?
A.$4
Hướng
dẫn
Đa phần các em thử bằng Table và được kết quả là $m=4$
Câu
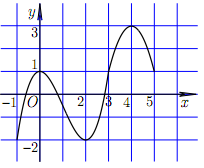
40. Cho hàm số $y=f(x)$ có đồ thị của hàm số $y=f'(x)$
được cho như hình bên. Hàm số $y=-2f(2-x)+{{x}^{2}}$ nghịch biến trên khoảng A.$\left(
-1;0 \right)$ B.$\left( 0;2 \right)$
C.$\left(
-2;-1 \right)$ D.$\left( -3;-2 \right)$ |
|

Câu
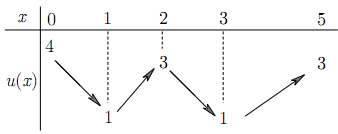
43. Cho hàm số $u\left( x \right)$ liên tục trên
đoạn $\left[ 0;5 \right]$ và có bảng biến thiên như hình vẽ. Có bao nhiêu giá
trị nguyên của m để phương trình $\sqrt{3x}+\sqrt{10-2x}=m.u(x)$ có nghiệm trên
đoạn $\left[ 0;5 \right]$ ? A.5 B.6
C.3 D.4 |
|
Hướng
dẫn
$\sqrt{3x}+\sqrt{10-2x}=m.u(x)\Leftrightarrow
g(x)=\frac{\sqrt{3x}+\sqrt{10-2x}}{u(x)}=m$
Để phương trình có nghiệm thì : $Mi{{n}_{g(x)}}\le m\le Ma{{x}_{g(x)}}$

Câu
46. Cho hàm số $y=f(x)$ có đạo hàm liên tục trên
R, $f(0)=0$ và $f(x)+f\left( \frac{\pi }{2}-x \right)=sinxcosx$ , với mọi $x\in
R$ . Giá trị của tích phân $\int\limits_{0}^{\frac{\pi }{2}}{xf'(x)dx}$ bằng ?
A.$\frac{-\pi }{4}$ B.$\frac{1}{4}$ C.$\frac{\pi }{4}$ D.$\frac{-1}{4}$

Câu
47.Cho
các số phức $w,z$ thỏa mãn $\left| w+i \right|=\frac{3\sqrt{5}}{5}$ và $5w=\left(
2+i \right)\left( z-4 \right)$ , Giá trị lớn nhất của biểu thức $P=\left|
z-1-2i \right|+\left| z-5-2i \right|$ bằng ?
A.$4\sqrt{3}$ B.$4+2\sqrt{13}$ C.$2\sqrt{53}$ D.$6\sqrt{7}$
Hướng
dẫn
$\left| w+i
\right|=\frac{3\sqrt{5}}{5}\Rightarrow \left| 5w+5i
\right|=3\sqrt{5}\Rightarrow \left| \left( 2+i \right)\left( z-4 \right)+5i
\right|=3\sqrt{5}$
$\Leftrightarrow \left| \left( 2+i
\right)z-8+i \right|=3\sqrt{5}\Leftrightarrow \left| \left( 2+i \right)\left(
z+\frac{-8+i}{2+i} \right) \right|=3\sqrt{5}$
$\left| 2+i \right|.\left| z+\frac{-8+i}{2+i}
\right|\Leftrightarrow \left| z-3+2i \right|=3\Leftrightarrow {{\left( x-3
\right)}^{2}}+{{\left( y+2 \right)}^{2}}=9\Rightarrow y=-2\pm \sqrt{9-{{\left(
x-3 \right)}^{2}}}$
Xét trường hợp $y=-2+\sqrt{9-{{\left( x-3
\right)}^{2}}}$