Giải chi tiết đề thi thử Thanh Chương 3 - Nghệ An lần 1 năm 2018
Đề thi có nhiều câu khá là hay, các em rèn luyện và xem full lời giải tại đây : Bấm vào đây
Một số câu hay trong đề
Câu 1. Cho hàm số \[y=f\left( x \right)\]có đạo hàm liên tục trên khoảng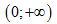
biết \[f'\left( x \right)+\left( 2x+3 \right){{f}^{2}}\left( x \right)=0,f\left( x \right)>0,\forall x>0\] và \[f\left( 1 \right)=\frac{1}{6}.\]Tính giá trị của \[P=1+f\left( 1 \right)+f\left( 2 \right)+...+f\left( 2017 \right)\]
A.$\frac{6059}{4038}$ B.$\frac{6055}{4038}$ C.$\frac{6053}{4038}$ D.$\frac{6047}{4038}$
Hướng dẫn
Ta có $f'\left( x \right)+\left( 2x+3 \right){{f}^{2}}\left( x \right)=0\Leftrightarrow -\frac{f'\left( x \right)}{{{f}^{2}}\left( x \right)}=2x+3\Leftrightarrow \int{-\frac{f'\left( x \right)}{{{f}^{2}}\left( x \right)}=\int{\left( 2x+3 \right)dx}}$
$\Leftrightarrow \int{-\frac{d\left( f\left( x \right) \right)}{{{f}^{2}}\left( x \right)}={{x}^{2}}+3x+C\Leftrightarrow \frac{1}{f\left( x \right)}={{x}^{2}}+3x+C\Leftrightarrow f\left( x \right)=\frac{1}{{{x}^{2}}+3x+C}}$ mà $f\left( 1 \right)=\frac{1}{6}\Rightarrow C=2$
Câu 2. Biết $\int\limits_{\frac{2\pi }{3}}^{\pi }{\frac{1-x\tan \,x}{{{x}^{2}}\cos x+x}dx=\ln \frac{\pi -a}{\pi -b}}\left( a;b\in \mathbb{Z} \right)$là. Tính $P=a+b$ ?
A.$P=2$ B.$P=-4$ C.$P=4$ D.$P=-2$
Hướng dẫn
Ta có $\frac{1-x\tan \,x}{{{x}^{2}}\cos x+x}=\frac{\frac{\cos x-x\sin x}{\cos x}}{{{x}^{2}}\cos x+x}=\frac{\cos x-x\sin x}{x\cos x\left( x\cos x+1 \right)}$
Đặt $t=x\,\cos x\Rightarrow dt=\cos x-x\sin x$
Đổi cận suy ra \[I=\int\limits_{-\frac{1}{3}}^{-\pi }{\frac{dt}{t\left( t+1 \right)}=\left. \ln \left| \frac{t}{t+1} \right| \right|}_{-\frac{1}{3}}^{-\pi }=\ln \left| \frac{\pi -3}{\pi -1} \right|\Rightarrow a=3;b=1\]
Câu 3. Tìm m để hàm số $f\left( x \right)=-{{x}^{3}}-mx+\frac{3}{28{{x}^{7}}}$ nghịch biến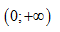 
A.$m\le -\frac{15}{4}$ B.$-\frac{15}{4}\le m\le 0$ C.$m\ge -\frac{15}{4}$ D.$-\frac{15}{4} < m\le 0$
Hướng dẫn
Ta có $f\left( x \right)=-{{x}^{3}}-mx+\frac{3}{28{{x}^{7}}}\Rightarrow f'\left( x \right)=-3{{x}^{2}}-m-\frac{3}{4{{x}^{8}}};\forall x>0$
Hàm số nghịch biến trên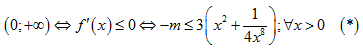 
Lại có ${{x}^{2}}+\frac{1}{4{{x}^{8}}}=\frac{{{x}^{2}}}{4}+\frac{{{x}^{2}}}{4}+\frac{{{x}^{2}}}{4}+\frac{{{x}^{2}}}{4}+\frac{1}{4{{x}^{8}}}\ge 5\sqrt[5]{{{\left( \frac{{{x}^{2}}}{4} \right)}^{4}}.\frac{1}{4{{x}^{8}}}}=\frac{5}{4}\Rightarrow \min \left\{ {{x}^{2}}+\frac{1}{4{{x}^{8}}} \right\}=\frac{5}{4}$
Vậy 
