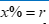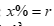Bài toán ứng dụng thực tế hàm số mũ, hàm số logarit trong thực tế

Bài 1: (THPT Nguyễn Tất Thành- Hà Nội-2017) Ông A gửi 15 triệu đồng vào ngân hàng theo thể thức lãi kép kỳ hạn 1 năm với lãi suất 7,65% / năm. Giả sử lãi suất không thay đổi. Hỏi sau 5 năm ông A thu được cả vốn lẫn lãi là bao nhiêu triệu đồng?

Hướng dẫn giải

Chọn D

Áp dụng công thức 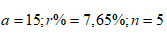 ta được:

Số tiền ông A có được sau 5 năm là: ${{A}_{5}}=15{{\left( 1+0,0765 \right)}^{5}}$triệu đồng.

Bài 2: (Sở GD&ĐT Lâm Đồng-2017) Ông B hửi vào ngân hàng số tiền là 120 triệu đồng với lãi suất định kỳ hàng năm là 12% /năm.Nếu sau mỗi năm ông không đến ngân hàng lấy lãi thì tiền lãi sẽ được cộng dồn vào vốn ban đầu. Hỏi sau đúng 12 năm kể từ ngày gửi, số tiền lãi L ( không kể vốn) ông sẽ nhận được bao nhiêu? ( Giả sử trong thời gian đó, lãi suất ngân hàng không thay đổi)

A.    $L={{12.10}^{7}}.\left[ {{\left( 1,12 \right)}^{12}}-1 \right]$ (VNĐ)

B.     $L={{12.10}^{7}}.\left[ {{\left( 1,12 \right)}^{12}}+1 \right]$ (VNĐ)       \[\]

C.    $L={{12.10}^{7}}.{{\left( 1,12 \right)}^{12}}$ (VNĐ)

D.    $L={{12.10}^{7}}.0,12$ (VNĐ)

Đáp án A

Bài 3: (THPT chuyên Lam Sơn-2017)Kết quả thống kê cho ở thời điểm 2013 dân số Việt Nam là 90 triệu người, tốc độ tăng trưởng dân số là 1,1%/ năm. Nếu mức tăng dân số ổn định như mức ở trên thì dân số Việt Nam sẽ gấp đôi ( đạt ngưỡng 180 triệu người) vào năm nào?

Đáp án B

Bài 3: (THPT chuyên Phan Bội Châu- Nghệ An-2017): Ông Quang cho ông Tèo vay 1 tỉ đồng với lãi xuất hàng tháng là 0,5%theo hình thức tiền lãi hàng tháng được cộng dồn vào tiền gốc cho tháng kế tiếp. Sau 2 năm, ông Tèo phải trả cho ông Quang cả gốc lẫn lãi. Hỏi số tiền ông Tèo phải trả là bao nhiêu? ( Làm tròn đến hàng nghìn)

Đáp án C

Bài 1: (THPT Quang Trung- Hà Nội-2017) Một người có 10 triệu đồng gửi vào ngân hàng với kỳ hạn 3 tháng ( 1 quý gồm 3 tháng), lãi suất 6%/ 1 quý theo hình thức lãi kép ( sau 3 tháng sẽ tính lãi cộng vào gốc). Sau đúng 3 tháng, người đó gửi thêm vào 20 triệu đồng cũng với hình thức lãi suất như vậy. Hỏi sau 1 năm, tính từ lần gửi đầu tiên, người đó nhận được số tiền là bao nhiêu?

Hướng dẫn giải

Chọn C

Sau quý thứ nhất, số tiền trong tài khoản của người đó là:

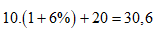triệu đồng ( do người đó gửi thêm vào 20 triệu).

Sau quý thứ hai số tiền có trong tài khoản của người đó là:

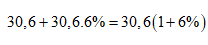triệu đồng.

Sau 1 năm số tiền người đó thu được là: 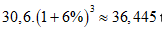triệu đồng.

Bài 2: (THPT chuyên Trần Phú- Hải Phòng lần II-2017) Một bác nông dân vừa bán một con trâu được số tiền là 20.000.000 đồng. Do chưa cần dùng đến tiền nên bác nông dân mang toàn bộ số tiền đó đi gửi tiết kiệm ngân hàng loại kỳ hạn 6 tháng với lãi suất kép là 8,5% một năm. Hỏi sau 5 năm 8 tháng bác nông dân nhận được bao nhiêu tiền cả vốn lẫn lãi ( làm tròn đến hàng đơn vị)? Biết rằng bác nông dân đó không rút vốn cũng như lãi trong tất cả các định kỳ trước và nếu rút trước thời hạn thì ngân hàng trả lãi suất theo không kỳ hạn 0,01% một ngày (1 tháng tính 30 ngày).

Đáp án A

Bài 3: (THPT chuyên Nguyễn Trãi- Hải Dương-2017) Một người đem gửi tiết kiệm ở ngân hàng với lãi suất 12%/ năm. Biết rằng cứ sau mỗi quý ( 3 tháng) thì lãi sẽ được cộng dồn vào gốc. Hỏi sau ít nhất bao nhiêu năm người đó nhận được số tiền( cả gốc và lãi) gấp 3 lần số tiền ban đầu?

Đáp án C

Bài 4: (THPT Lạng Giang số 1- Bắc Giang-2017) Một người lần đầu gửi vào ngân hàng 100 triệu đồng với kỳ hạn 3 tháng, lãi suất 2% một quý theo hình thức lãi kép. Sau 6 tháng , người đó gửi thêm 100 triệu đồng với kì hạn và lãi suất nhưu trước đó. Tổng số tiền người đó nhận được 1 năm sau khi gửi thêm tiền gần nhất với kết quả nào sau đây?

Đáp án C

Bài 1: (THPT Huỳnh Thúc Kháng-2017) Một người gửi tiết kiệm theo thể thức lãi kép như sau: Mỗi tháng người này gửi tiết kiệm một số tiền là a đồng rồi gửi vào ngân hàng theo kì hạn một tháng với lãi suất là 0,6%/tháng. Tìm a để sau 3 năm kể từ ngày gửi tiền lần đầu người đó có tổng số tiền là 400 triệu đồng. (Biết lãi suất không thay đổi trong suốt thời gian gửi)

Hướng dẫn giải

Chọn D

Áp dụng công thức trên ta có sau ba năm kể từ ngày gửi lần đầu tiên số tiền nhận được là:

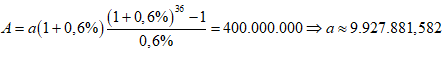 đồng.

Bài 2: (THPT Lê Quý Đôn- Hà Nội-2017) Ông An gửi tiết kiệm tích lũy cho con tại một ngân hàng với ố tiền tiết kiệm ban đầu là 200.000.000 VNĐ với lãi suất 7%/ năm. Từ năm thứ hai trử đi, mỗi năm ông gửi thêm vào tài khoản tiết kiệm với số tiền là 20.000.000 đồng. Ông không rút lãi định kỳ hàng năm. Biết rằng lãi suất định kỳ hàng năm không thay đổi. Hỏi sau 18 năm, số tiền ông An nhận được cả gốc lẫn lãi là bao nhiêu?

Đáp án A

Bài 3: (THPT chuyên Quốc Học Huế-2017) Bạn Nam là sinh viên của một trường đại học, muốn vay tiền ngân hàng với lãi suất ưu đãi trang trải kinh phí học tập hàng năm. Đầu mỗi năm học, bạn ấy vay ngân hàng với số tiền là10 triệu đồng với lãi suất là 4%. Tính số tiền mà Nam nợ ngân hàng sau 4 năm, biết rằng trong 4 năm đó, ngân hàng không thay đổi lãi suất? ( kết quả làm tròn đến hàng nghìn đồng)

Đáp án B

Bài 4: (THPT Chuyên Lương Văn Tụy -2017) Một bà mẹ Việt Nam anh hùng được hưởng số tiền là 4 triệu đồng trên một tháng ( chuyển vào tải khoản của mẹ ở ngân hàng vào đầu tháng). Từ tháng 1 năm 2016 mẹ không rút đi rút tiền mà để lại ngân hàng và được tính lãi suất 1% trên tháng. Đến đầu tháng 12 năm 2016 mẹ rút toàn bộ số tiền trên ( gồm số tiền gốc và lãi). Hỏi khi đó mẹ linh vè bao nhiêu tiền? ( Kết quả làm tròn theo đơn vị nghìn đồng)

           A. 50 triệu 730 nghìn đồng

B.       B.  50 triệu 640 nghìn đồng

C        C. 53 triệu 760 nghìn đồng

D.        D.   48 triệu 480 nghìn đồng

Đáp án A

Bài 1: ( đề thi minh họa BGD lần 1- năm 2017) Ông A vay ngân hàng 100 triệu đồng với lãi suất 12% / năm. Ông muốn hoàn nợ cho ngân hàng theo cách: Sau đúng một tháng kể từ ngày vay, ông bắt đầu hoàn nợ; hai lần hoàn nợ liên tiếp cách nhau đúng 1 tháng và số tiền hoàn nợ mỗi tháng là như nhau và trả hết nợ sau đúng 3 tháng kể từ ngày vay.Hỏi theo cách đó, số tiền m ông A sẽ phải trả cho ngân hàng hàng tháng trong mỗi lần hoàn nợ là bao nhiêu? Biết rằng lãi suất ngân hàng không thay đổi trong thời gian ông A hoàn nợ.

Hướng dẫn giải

Chọn B

Lãi suất 12% trên một năm vậy 1 tháng có lãi suất là 1%

Áp dụng công thức trên suy ra số tiền m ông A phải trả mỗi tháng là:

$a=\frac{A{{\left( 1+r \right)}^{n}}.r}{{{\left( 1+r \right)}^{n}}-1}=\frac{100{{\left( 1+0,01 \right)}^{3}}.0,01}{{{\left( 1+0,01 \right)}^{3}}-1}=\frac{{{\left( 1,01 \right)}^{3}}}{{{\left( 1,01 \right)}^{3}}-1}$

Bài 2: (sở GD&DT Bắc Ninh-2017) Chị Minh vay ngân hàng 300 triệu đồng theo phương thức trả góp để mau nhà. Nếu cuối mỗi tháng, bắt đầu từ tháng thứ nhất chị Minh trả 5,5 triệu đồng và chịu lãi số tiền chưa trả là 0,5% trên một tháng( biết lãi suất không thay đổi) thì sau bao lâu chị Minh trả hết số tiền trên?

Đáp án A

Bài 3: (sở GD&DT Nam Định)  Anh Nam vay ngân hàng 1 tỷ đồng theo phương thức trả góp ( chịu lãi số tiền chưa trả) với lãi suất là 0,5%/ tháng. Nếu cuối mỗi tháng bắt đầu từ tháng thứ nhất anh Nam trả 30 triệu đồng. Hỏi sau bao nhiêu tháng anh Nam trả hết nợ.

Đáp án C

Bài 1:Một người lĩnh lương khởi điểm là A đồng/ tháng. Cứ 3 tháng người đó được tăng lương thêm 7%/tháng. Hỏi sau 36 năm thì người đó lĩnh được tất cả bao nhiêu tiền?

Hướng dẫn giải

Chọn A

Áp dụng công thức ta đươc: ${{T}_{36}}={{3.10}^{6}}.12.\frac{{{\left( 1,07 \right)}^{12}}-1}{0,07}\approx 643984245,8$ triệu đồng

Bài 2: Một người lĩnh lương khởi điểm là 2.000.000 đồng/ tháng. Cứ 3 năm người đó được tăng lương thêm 7%/năm. Hỏi sau bao nhiêu  năm thì người đó lĩnh được 1.800.000.000 đồng?

 Đáp án C

Bài 1: (THPT Kim Liên -Hà Nội- 2017) Dân số thế giới được tính theo công thức $S=A.{{e}^{r.N}}$ trong đó: A là dân số của năm lấy mốc tính, S là dân số sau N năm, r là tỷ lệ tăng dân số hằng năm. Cho biết năm 2001, dân số Việt Nam có khoảng 78.685.000 người và tỷ lệ tăng dân số hàng năm là 1,7%/ năm. Như vậy, nếu tỷ lệ tăng dân số hàng năm không đổi thì đến năm bao nhiêu dân số nước ta ở khoảng mức 120 triệu người?

Hướng dẫn giải

Chọn C

Áp dụng công thức trên ta được: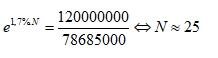 

Như vậy sau 25 năm tức là vào năm 2026 thì dân số ở nước ta đạt mức 120 triệu người.

Bài 2: (THPT chuyên Nguyễn Bỉnh Khiêm-2017) Sự tăng trưởng của một loại vi khuẩn được tính theo công thức $S=A.{{e}^{r.N}}$, trong đó A là lượng vi khuẩn ban đầu, r là tỷ lệ tăng trưởng(r>0), t là thời gian tăng trưởng. Biết số lượng vi khuẩn ban đầu là 100 con và sau 5 giờ là 300 con. Hỏi sau 15 giờ có bao nhiêu con vi khuẩn?

Đáp án B

Bài 1: (THPT Nguyễn Văn Linh) Bom nguyên tử là loại bom chưa Uranium-235 được phát nổ khi ghép các khối Uranium-235 thành một khối chưa 50kg tinh khiết. Uranium-235 có chu kì bán rã là 704 triệu năm. Nếu quả bom ban đầu chứa 64kg Uranium-235 tinh khiết và sau t triệu năm thì quả bom không thể phát nổ. Khi đó t thỏa mãn phương trình:

Hướng dẫn giải

Chọn A

Ở đây sau t triệu năm thì quả bom không thể phát nổ, tức là trong khoảng thời gian t triệu năm đó thì quả bom đó không nổ, quả bom nổ vào năm thứ t triệu tính từ thời điểm ban đầu.

Do chu kì bán rã của quả bom là 704 triệu năm nên ta có: $704=\frac{\ln 2}{k}\Rightarrow k=\frac{\ln 2}{704}$

Sau t triệu năm quả bom không phát nổ nên $64.{{e}^{-\frac{\ln 2}{704}.t}}=50\Rightarrow {{e}^{-\frac{\ln 2}{704}.t}}=\frac{50}{64}\Leftrightarrow \frac{50}{64}={{\left( \frac{1}{2} \right)}^{\frac{t}{704}}}$

Bài 2: (THPT Lương Thế Vinh – Hà Nội-2017) Một chất phóng xạ theo thời gian sẽ phaanhuyr tự nhiên. Công thức tính khối lượng chất phóng xạ Cacbon ${{C}^{14}}$ còn lại sau thời gian t năm là $m\left( t \right)={{m}_{0}}.{{e}^{-1,{{21.10}^{4}}.t}}$ với ${{m}_{0}}$ là khối lượng Cacbon ban đầu. Người ta tìm trong một mẫu đồ cổ có một lượng Cacbon và xác định nó đã mất đi 15% lượng Cacbon ban đầu của nó. Hỏi mẫu đồ cổ đó cao độ tuổi là bao nhiêu năm?

Đáp án B

.

Bài viết gợi ý: