Câu
48: Trong thư viện có 3 quyển sách toán, 3 quyển sách lý, 3
quyển sách hóa, 3 quyển sách sinh. Biết các quyển sách cùng môn giống nhau, xếp
12 quyển sách trên lên giá thành một hàng sao cho không có 3 quyển nào cùng môn
đứng cạnh nhau. Hỏi có tất cả bao nhiêu cách xếp?
A. $308664$. B. $16800$. C. $369600$. D. $295176$.
Hướng dẫn giải
Chọn A
Số cách xếp 12 quyển sách lên giá sách là: $\frac{12!}{{{\left(
3! \right)}^{4}}}$
Vì các loại sách có vai trò như nhau, nên số cách xếp 3
cuốn liền nhau của 1 loại sách là:
$\frac{10!}{{{\left( 3! \right)}^{3}}}$ ⇒ cả 4 loại có: $4.\frac{10!}{{{\left( 3! \right)}^{3}}}$
Số cách xếp mà trong đó có 2 loại mỗi loại 3 cuốn liền
nhau là:$C_{4}^{2}.\frac{8!}{{{\left( 3! \right)}^{2}}}$
Số cách xếp mà trong đó 3 loại mỗi loại 3 cuốn liền nhau
là:$C_{4}^{3}.\frac{6!}{3!}$
Số cách xếp cả 4 loại mỗi loại 3 cuốn liền nhau là: $4!$
Áp dụng nguyên lý bao hàm và loại trừ, ta có số cách xếp
theo yêu cầu đề bài là:
$\frac{12!}{{{\left( 3! \right)}^{4}}}-4.\frac{10!}{{{\left( 3! \right)}^{3}}}+C_{4}^{2}.\frac{8!}{{{\left( 3! \right)}^{2}}}-C_{4}^{3}.\frac{6!}{3!}+4!=308664$
A. ${{a}^{2}}-xy=a(x+y)$. B. ${{a}^{2}}+xy=a(x+y)$.
C. $2{{a}^{2}}-xy=2a(x+y)$. D. $2{{a}^{2}}+xy=2a(x+y)$.
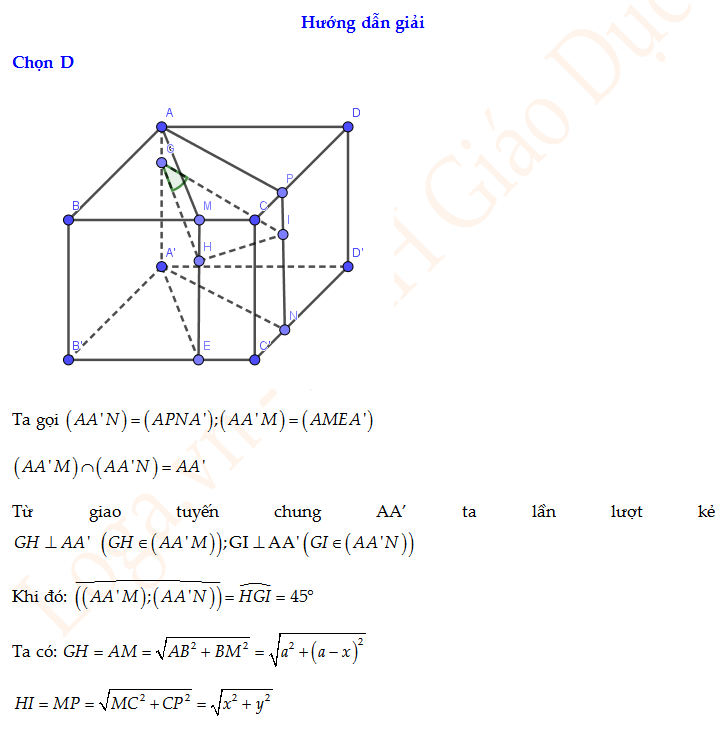
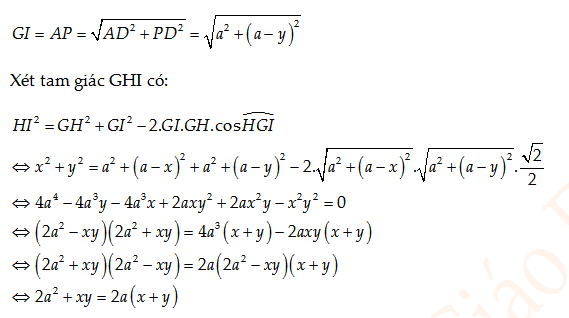
Câu 38: Cho hàm số $f(x)={{x}^{3}}-(2m+1){{x}^{2}}+3mx-m$ có đồ thị $({{C}_{m}})$. Có bao nhiêu giá trị
nguyên của tham số $m$ thuộc $(-2018;2018]$ để đồ thị $({{C}_{m}})$có hai điểm
cực trị nằm khác phía so với trục hoành.
A. $4033$. B. $4034$. C. $4035$. D. $4036$.









