Vừa hôm 30/5 thì SGD Nam Định đã tổ chức thi thử lần 2, đề khá là vừa tầm nhiều câu phân loại đã được anh hướng dẫn trong sách Bí Kíp Thế Lực 2018 v3
4 Câu này đều giống các dạng đã hướng dẫn trong sách ver3 nên các em cứ yên tâm học.
Câu
47.Cho phương trình $\left( \sqrt{x}+\sqrt{x-1}
\right)\left( m\sqrt{x}+\frac{1}{\sqrt{x-1}}+16\sqrt[4]{{{x}^{2}}-x} \right)=1$
, với m là tham số thực. Tìm số các giá trị nguyên của tham số m để phương
trình đã cho có hai nghiệm thực phân biệt
A.11 B.9
C.20 D.4
Hướng
dẫn: CASIO EXPERT : Nguyễn Thế Lực
$\left(
\sqrt{x}+\sqrt{x-1} \right)\left( m\sqrt{x}+\frac{1}{\sqrt{x-1}}+16\sqrt[4]{{{x}^{2}}-x}
\right)=1$
$\to
m\sqrt{x}=\frac{1}{\sqrt{x}+\sqrt{x-1}}-\frac{1}{\sqrt{x-1}}-16\sqrt[4]{{{x}^{2}}-x}$
$\leftrightarrow
m=\frac{1}{\sqrt{x}}\left(
\frac{1}{\sqrt{x}+\sqrt{x-1}}-\frac{1}{\sqrt{x-1}}-16\sqrt[4]{{{x}^{2}}-x}
\right)$
Các em dùng Table lập BBT với Start 1.000001= End 8= Step 0.25=
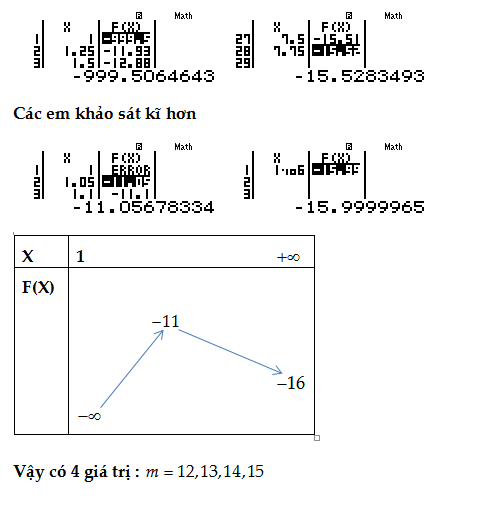
Câu
48. Có tất cả bao nhiêu giá trị nguyên dương của
m để phương trình ${{5}^{{{\sin }^{2}}x}}+{{6}^{{{\cos }^{2}}x}}={{7}^{{{\cos
}^{2}}x}}.{{\log }_{2}}m$ có nghiệm ?
A.63
B.64 C.6 D.62
Hướng
dẫn
\[{{5}^{{{\sin
}^{2}}x}}+{{6}^{{{\cos }^{2}}x}}={{7}^{{{\cos }^{2}}x}}.{{\log }_{2}}m\]
\[\Leftrightarrow {{\log }_{2}}m=\frac{{{5}^{{{\sin }^{2}}x}}+{{6}^{{{\cos }^{2}}x}}}{{{7}^{{{\cos }^{2}}x}}}\to 1\le {{\log }_{2}}m\le 6\to 2\le m\le 64\]
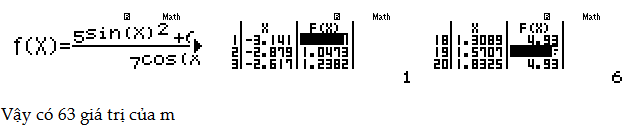
Câu
49. Cho hàm số $f(x)$ có đạo hàm liên tục
trên $\left( 0;+\infty \right)$ , biết
$f'\left( x \right)+\left( 2x+4
\right){{f}^{2}}\left( x \right)=0,f\left( x \right)>0\forall x>0,f\left(
2 \right)=\frac{1}{15}$ . Tính $f(1)+f(2)+f(3)$
A.$\frac{7}{15}$ B.$\frac{11}{15}$ C.$\frac{11}{30}$ D.$\frac{7}{30}$
Hướng
dẫn: CASIO EXPERT : Nguyễn Thế Lực
$f'\left( x \right)+\left( 2x+4
\right){{f}^{2}}\left( x \right)=0\Leftrightarrow -\frac{f'\left( x
\right)}{{{f}^{2}}\left( x \right)}=2x+4\Rightarrow \frac{1}{f\left( x \right)}={{x}^{2}}+4x+C$
$f(2)=\frac{1}{15}\to 15=4+8+C\to C=3\Rightarrow \frac{1}{f\left( x \right)}={{x}^{2}}+4x+3\to f(x)=\frac{1}{{{x}^{2}}+4x+3}$
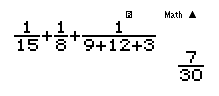
Câu
50. Cho số phức z thỏa mãn $\left| z-2+i
\right|+\left| z+1-i \right|=\sqrt{13}$ .Tìm giá trị nhỏ nhất m của biểu thức $\left|
z+2-i \right|$
A.$m=1$ B. $m=\frac{2\sqrt{13}}{13}$ C. $m=\frac{\sqrt{13}}{13}$ D. $m=\frac{1}{13}$
Hướng
dẫn: Giống câu 9 trang 176 sách BKTLver3
Các em xét : $\left| z+2-i \right|=A\to
{{\left( x+2 \right)}^{2}}+{{\left( y-1 \right)}^{2}}={{A}^{2}}\to y=1\pm
\sqrt{{{A}^{2}}-{{\left( x+2 \right)}^{2}}}$
Sau đó các em xét các đáp án từ nhỏ tới lớn
thế vào $\left| z-2+i \right|+\left| z+1-i \right|=\sqrt{13}$ giải phương trình
xem có tồn tại số phức thỏa mãn hay không
$\left| z-2+i \right|+\left| z+1-i \right|=\sqrt{13}\Rightarrow \sqrt{{{\left( x-2 \right)}^{2}}+{{\left( y+1 \right)}^{2}}}+\sqrt{{{\left( x+1 \right)}^{2}}+{{\left( y-1 \right)}^{2}}}=\sqrt{13}$








