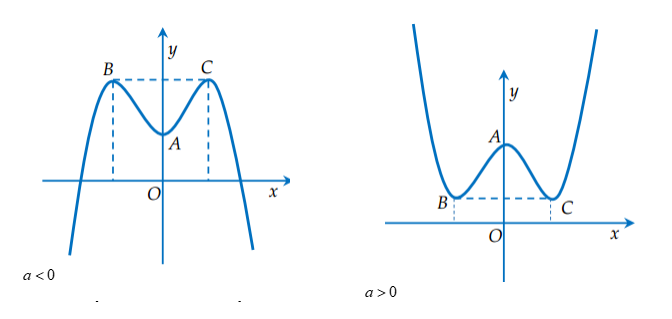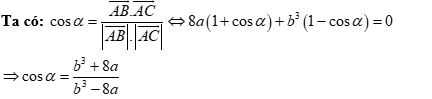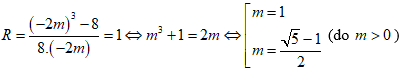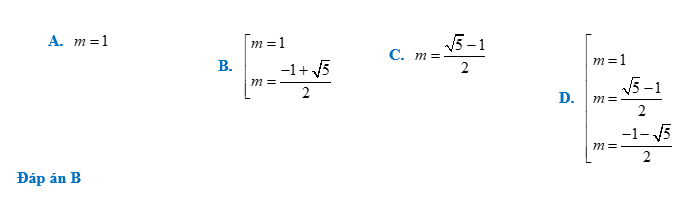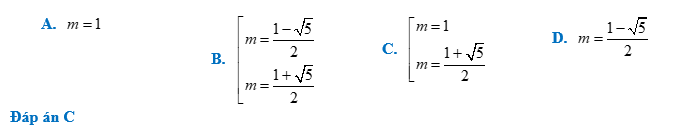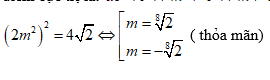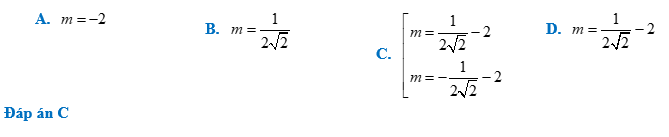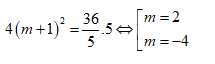Hướng dẫn giải
$AB=BC=AC$
$\Rightarrow
\frac{{{b}^{3}}}{a}=-24$
Bài 1:
Tìm m để hàm số $y={{x}^{4}}-2m{{x}^{2}}+2m+{{m}^{4}}$ có ba điểm cực
trị tạo thành một tam giác đều.
Hướng dẫn giải
Ta
có: $a=1;b=-2m$
- Điều
kiện để có ba điểm cực trị là $ab<0\Leftrightarrow -2m<0\Leftrightarrow
m>0$
- Điều
kiện tạo thành một tam giác đều là : $\frac{{{\left( -2m
\right)}^{3}}}{1}=-24\Leftrightarrow {{m}^{3}}=3\Leftrightarrow
m=\sqrt[3]{3}$
Bài 2:
Tìm m để hàm số $y=\frac{9}{8}{{x}^{4}}+3\left( m-2017 \right){{x}^{2}}-2018$
có 3 cực trị tạo thành một tam giác đều
|
A. $m=2016$
|
B. $m=2017$
|
C. $m=2018$
|
D. $m=2019$
|
Bài 3:
Tìm m để đồ thị hàm số $\left( {{C}_{m}} \right)\,\,y={{x}^{4}}+2\left( m-2 \right){{x}^{2}}+{{m}^{2}}-5m+5$
có 3 điểm cực trị tạo thành tam giác đều:
|
A. $m=2-\sqrt[3]{3}$
|
B. $m=2+\sqrt[3]{3}$
|
C. $m=5-2\sqrt[3]{3}$
|
D. $m=5+2\sqrt[3]{3}$
|
Bài toán 3 : Tìm tất cả các giá trị của tham số m để
đồ thị hàm số $y=a{{x}^{4}}+b{{x}^{2}}+c\,\,\,\left( a\ne 0 \right)$ có ba
điểm cực trị tạo thành tam giác có diện tích ${{S}_{0}}$
Hướng dẫn giải
${{S}_{ABC}}=\frac{1}{2}.h.BC\Rightarrow
S_{0}^{2}=\frac{-{{b}^{5}}}{32{{a}^{3}}}$
Bài 1: Tìm
m để đồ thị hàm số $y={{x}^{4}}-2m{{x}^{2}}+m+1$ có 3 điểm cực trị tạo thành
một tam giác có diện tích bằng 32.
Hướng dẫn giải:
- Điều
kiện để có 3 điểm cực trị là: $ab<0\Leftrightarrow -2m<0\Leftrightarrow
m>0$
- Điều
kiện để tam giác có diện tích bằng 32 là: ${{32}^{2}}=\frac{-{{\left( -2m
\right)}^{5}}}{32}\Leftrightarrow {{m}^{5}}={{32}^{2}}\Leftrightarrow m=4$ (
thỏa mãn)
Bài 2: Cho
hàm số $y={{x}^{4}}+2m{{x}^{2}}-m-1$ . Tìm m để hàm số có 3 điểm cực trị tạo
thành một tam giác có diện tích bằng $4\sqrt{2}$
|
A. $m=2$
|
B. $m=-2$
|
C. $m=4$
|
D. $m=-4$
|
Bài 3: Tìm
m để đồ thị hàm số $y=3{{x}^{4}}-2m{{x}^{2}}+2m+{{m}^{4}}$ có 3 điểm cực trị
tạo thành một tam giác có diện tích bằng 3
|
A. $m=3$
|
B. $m=-3$
|
C. $m=4$
|
D. $m=-4$
|
Bài 4: (THPT QG- 2017) Tìm tất cả các giá trị
thực của tham số m để đồ thị hàm số $y={{x}^{4}}-2m{{x}^{2}}$ có ba điểm cực
trị tạo thành một tam giác có diện tích nhỏ hơn 1
|
A. $0<>
|
B. $m<1$
|
C. $0<>
|
D. $m>0$
|
|
Bài 2: B
|
Bài 3: B
|
Bài 4: C.
|
Bài toán 4:Tìm tất cả các giá trị của tham số m để đồ
thị hàm số $y=a{{x}^{4}}+b{{x}^{2}}+c\,\,\,\left( a\ne 0 \right)$ có ba điểm
cực trị tạo thành tam giác có diện tích lớn nhất .
Hướng dẫn giải
Ta
chỉ việc tìm max của $-\frac{{{b}^{5}}}{32{{a}^{3}}}$
Bài 1: Cho
hàm số $y={{x}^{4}}-2\left( 1-{{m}^{2}} \right){{x}^{2}}+m+1$ . Tìm m để hàm
số có 3 cực trị tạo thành tam giác có diện tích lớn nhất
Hướng dẫn giải
- Điều
kiện hàm số có 3 điểm cực trị là: $ab<0\Leftrightarrow -2\left(
1-{{m}^{2}} \right)<0\Leftrightarrow -1\le m\le 1$
- Diện
tích của tam giác là: $S_{0}^{2}=\frac{-{{\left( -2\left( 1-{{m}^{2}} \right)
\right)}^{5}}}{32}={{\left( 1-{{m}^{2}} \right)}^{5}}$
- Khi
diện tích ${{S}_{0}}$ thì $S_{0}^{2}$ cũng max. Vậy ${{\left( 1-{{m}^{2}}
\right)}^{5}}$ max $\Leftrightarrow 1-{{m}^{2}}\le 1\Leftrightarrow m=0$
- Vậy
${{S}_{\max }}=1$
Bài 2: Cho
hàm số $y={{x}^{4}}-2\left( 1-{{m}^{2}} \right){{x}^{2}}+m+1$. Tìm m để hàm
số có 3 điểm cực trị tạo thành một tam giác có diện tích lớn nhất.
|
A. Không có m
tm
|
B. $m=0$
|
C. $m=1$
|
D. $m=-1$
|
Đáp án B
Bài toán 5: Tìm tất cả các giá trị của tham số m để đồ
thị hàm số $y=a{{x}^{4}}+b{{x}^{2}}+c\,\,\,\left( a\ne 0 \right)$ có ba điểm
cực trị tạo thành tam giác có góc ở đỉnh cân bằng 𝛂.
Hướng dẫn giải
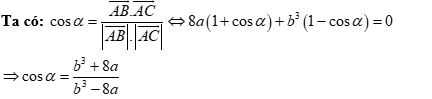
$\Rightarrow
\cos \alpha =\frac{{{b}^{3}}+8a}{{{b}^{3}}-8a}$
Hoặc:
$8a+{{b}^{3}}.{{\tan }^{2}}\frac{\alpha }{2}=0$
Bài 1:
Tìm m để đồ thị hàm số: $y={{x}^{4}}+2m{{x}^{2}}+{{m}^{2}}+m$ có 3 cực trị
tạo thành một tam giác có góc ở đỉnh bằng $120{}^\circ $
Hướng dẫn giải
- Điều
kiện để đồ thị hàm số có 3 điểm cực trị là: $ab<0\Leftrightarrow
2m<0\Leftrightarrow m<0$
- Điều
kiện để tam giác có góc ở đỉnh bằng $120{}^\circ $là: $\cos 120{}^\circ
=\frac{{{\left( 2m \right)}^{3}}+8}{{{\left( 2m \right)}^{3}}-8}=-\frac{1}{2}\Leftrightarrow
2\left( {{m}^{3}}+1 \right)=1-{{m}^{3}}\Leftrightarrow
3{{m}^{3}}=-1\Leftrightarrow m=\frac{-1}{\sqrt[3]{3}}$ ( thỏa mãn)
Bài 2:
Tìm tất cả các giá trị thực của m để đồ thị hàm số
$y={{x}^{4}}-4\left( m-1 \right){{x}^{2}}+2m-1$ có 3 cực trị tạo thành một
tam giác có góc ở đỉnh bằng $120{}^\circ $ .
|
A. $m=1+\sqrt[3]{16}$
|
B. $m=1+\sqrt[3]{2}$
|
C. $m=1+\sqrt[3]{48}$
|
D. $m=1+\sqrt[3]{24}$
|
Đáp án D
Bài toán 6: Tìm tất cả các giá trị của tham số m để đồ thị
hàm số $y=a{{x}^{4}}+b{{x}^{2}}+c\,\,\,\left( a\ne 0 \right)$ có ba điểm cực
trị tạo thành tam giác có ba góc là góc nhọn.
Hướng dẫn giải
Để
có ba góc là góc nhọn thì góc ở đỉnh cũng là góc nhọn $\cos \alpha =\frac{\overrightarrow{AB}.\overrightarrow{AC}}{\left|
\overrightarrow{AB} \right|.\left| \overrightarrow{AC} \right|}>0$
Mà
$\left| \overrightarrow{AB} \right|.\left| \overrightarrow{AC}
\right|>0\Leftarrow \overrightarrow{AB}.\overrightarrow{AC}>0\Leftrightarrow
b\left( {{b}^{3}}+8a \right)>0$
Bài toán 7: Tìm tất cả các giá trị của tham số m để đồ thị
hàm số $y=a{{x}^{4}}+b{{x}^{2}}+c\,\,\,\left( a\ne 0 \right)$ có ba điểm cực
trị tạo thành tam giác có bán kính đường tròn nội tiếp là r
Hướng dẫn giải
Ta
có: $S=pr\Rightarrow r=\frac{2S}{C}=\frac{{{b}^{2}}}{4.\left| a
\right|.\left( 1+\sqrt{1-\frac{{{b}^{3}}}{8a}} \right)}$ với C là chu vi của
tam giác.
Bài 1: Cho
hàm số $y={{x}^{4}}-2m{{x}^{2}}+2$.Tìm m để đồ thị hàm số có ba điểm cực trị
tạo thành một tam giác có bán kính đường tròn nội tiếp bằng 1.
Hướng dẫn giải
- Điều
kiện để đồ thị hàm số có 3 điểm cực trị là: $ab<0\Leftrightarrow
-2m<0\Leftrightarrow m>0$
- Điều
kiện có bán kính đường tròn nội tiếp bằng 1 là: $r=\frac{{{\left( -2m \right)}^{2}}}{4.1.\left(
1+\sqrt{1-\frac{{{\left( -2m \right)}^{3}}}{8}} \right)}=1\Leftrightarrow
4{{m}^{2}}=4.\left( 1+\sqrt{1+{{m}^{3}}} \right)\Leftrightarrow
{{m}^{2}}=1+\sqrt{1+{{m}^{3}}}\Leftrightarrow m=2$
Bài 2: Cho
hàm số $y={{x}^{4}}-2m{{x}^{2}}+2m+{{m}^{4}}$, với giá trị nào của m thì đồ
thị hàm số có ba điểm cực trị tạo thành một tam giác có bán kính đường tròn
nội tiếp bằng 2
|
A. $m=2+2\sqrt{2}$
|
B. $m=0$
|
C. $m=2-2\sqrt{2}$
|
D. $m=2\pm
2\sqrt{2}$
|
Đáp án A
Bài toán 8: Tìm tất cả các giá trị của tham số m để đồ thị
hàm số $y=a{{x}^{4}}+b{{x}^{2}}+c\,\,\,\left( a\ne 0 \right)$ có ba điểm cực
trị tạo thành tam giác có bán kính đường tròn ngoại tiếp là R.
Hướng dẫn giải
Ta
có: ${{S}_{ABC}}=\frac{AB.BC.CA}{4R}\Leftrightarrow \frac{1}{2}.AH.BC=\frac{AB.BC.CA}{4R}\Leftrightarrow
2.{{R}^{2}}.A{{H}^{2}}=A{{B}^{4}}\Leftrightarrow
R=\frac{{{b}^{3}}-8a}{8.\left| a \right|.b}$
Bài 1: Cho
hàm số $y={{x}^{4}}-2m{{x}^{2}}+m-1$ , tìm giá trị thực của m để đồ thị hàm
số đã cho có ba điểm cực trị tạo thành một tam giác có bán kính đường tròn
ngoại tiếp bằng 1.
Hướng dẫn giải
- Điều
kiện để đồ thị hàm số có 3 điểm cực trị là: $ab<0\Leftrightarrow
-2m<0\Leftrightarrow m>0$
Áp
dụng công thức ta có: 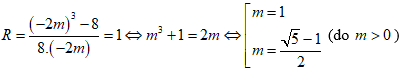
Bài 2: Cho
hàm số $y={{x}^{4}}-2m{{x}^{2}}-3$ , tìm giá trị thực của m để đồ thị hàm số
đã cho có ba điểm cực trị tạo thành một tam giác có bán kính đường tròn ngoại
tiếp nhỏ nhất.
|
A. $m=\frac{1}{\sqrt[3]{2}}$
|
B. $m=1$
|
C. $m=\sqrt[3]{2}$
|
D. $m=\frac{1}{2}$
|
Đáp án A
Bài toán 9: Tìm tất cả các giá trị của tham số m để đồ thị
hàm số $y=a{{x}^{4}}+b{{x}^{2}}+c\,\,\,\left( a\ne 0 \right)$ có ba điểm cực
trị tạo thành tam giác nhận gốc O làm trọng tâm.
Hướng dẫn giải
${{b}^{2}}-6ac=0$
Bài 1: cho
hàm số $y={{x}^{4}}-2{{x}^{2}}+m+2$ xác định giá trị của m đề đồ thị hàm số
đã cho có 3 điểm cực trị nhận gốc tọa độ O làm trọng tâm
Hướng dẫn giải
- Điều
kiện để hàm số có 3 điểm cực trị là: a\[ab<0\Leftrightarrow -2<0\left(
tm \right)\]
- Áp
dụng công thức có: ${{\left( -2 \right)}^{2}}-6.1.\left( m+2
\right)=0\Leftrightarrow 4-6m-12=0\Leftrightarrow m=\frac{-4}{3}$
Bài 2: Cho
hàm số $y={{x}^{4}}+2\left( m-4 \right){{x}^{2}}+m+5$ tìm m để đồ thị hàm số
đã cho có ba điểm cực trị tạo thành một tam giác có gốc tọa độ O làm trọng
tâm.
|
A. $m=0$
|
B. $m=2$
|
C. $m=1$
|
D. $m=-1$
|
Đáp án C
Bài toán 10: Tìm tất cả các giá trị của tham số m để đồ thị
hàm số $y=a{{x}^{4}}+b{{x}^{2}}+c\,\,\,\left( a\ne 0 \right)$ có ba điểm cực
trị tạo thành tam giác nhận O làm trực tâm.
Hướng dẫn giải
${{b}^{3}}+8a-4ac=0$
Bài 1: Cho
hàm số $y={{x}^{4}}-2m{{x}^{2}}-2$ tìm m để đồ thị hàm số đã cho có ba điểm
cực trị tạo thành một tam giác nhận gốc tọa độ O làm trực tâm.
Hướng dẫn giải
- Điều
kiện để hàm số đã cho có 3 điểm cực trị là: $ab<0\Leftrightarrow m>0$
- Áp
dụng công thức ta được: ${{\left( -2m \right)}^{3}}+8+8=0\Leftrightarrow
m=\sqrt[3]{2}$ ( thỏa mãn)
Bài 2: Cho
hàm số $y={{x}^{4}}-2m{{x}^{2}}+1-m$ , tìm tất cả các giá trị của m đề đồ thị
hàm số đã cho có ba điểm cực trị tạo thành một tam giác nhận gốc tọa độ O làm
trực tâm.
|
A. $m=1$
|
B. $m=2$
|
C. $m=0$
|
D. $m=-1$
|
Đáp án A
Bài toán 11: Tìm tất cả các giá trị của tham số m để đồ thị
hàm số $y=a{{x}^{4}}+b{{x}^{2}}+c\,\,\,\left( a\ne 0 \right)$ có ba điểm cực
trị tạo thành tam giác có độ dài cạnh $BC={{m}_{0}}$
Hướng dẫn giải
$am_{0}^{2}+2b=0$
Bài 1: Cho hàm
số $y={{x}^{4}}-2m{{x}^{2}}+1-m$ tìm tất cả các giá trị của m đề đồ
thị hàm số đã cho có ba điểm cực trị tạo thành một tam giác có độ dài cạnh
$BC=4$
Hướng dẫn giải
- Điều
kiện để hàm số có 3 điểm cực trị là: $ab<0\Leftrightarrow m>0$
- Áp
dụng công thức ta được: ${{4}^{2}}+2.\left( -2m \right)=0\Leftrightarrow m=4$
( thỏa mãn)
Bài 2: Cho
hàm số $y={{x}^{4}}-2\left( m+1 \right){{x}^{2}}+{{m}^{2}}+5m+7$ , tìm tất cả
các giá trị của m đề đồ thị hàm số đã cho có ba điểm cực trị tạo thành một
tam giác có độ dài cạnh $BC=8$
|
A. $m=8$
|
B. $m=16$
|
C. $m=15$
|
D. $m=-17$
|
Đáp án C
Bài toán 12: Tìm tất cả các giá trị của tham số m để đồ thị
hàm số $y=a{{x}^{4}}+b{{x}^{2}}+c\,\,\,\left( a\ne 0 \right)$ có ba điểm cực
trị tạo thành tam giác có cực trị $B,C\in Ox$
Hướng dẫn giải
${{b}^{2}}=4ac$
Bài 1: Cho
hàm số $y={{x}^{4}}-2{{x}^{2}}+2m$ , tìm tất cả các giá trị của m đề đồ thị
hàm số đã cho có ba điểm cực trị trong đó có hai cực trị thuộc trục hoành
Hướng dẫn giải
- Đồ
thị hàm số luôn có 3 điểm cực trị
- Áp
dụng công thức ta có: $4=4.2m\Leftrightarrow m=\frac{1}{2}$
Bài 2: Cho
hàm số $y=1008{{x}^{4}}-m{{x}^{2}}+1008$ , tìm tất cả các giá trị của m đề đồ
thị hàm số đã cho có ba điểm cực trị trong đó có hai cực trị thuộc trục
hoành.
|
A. $m=-1008$
|
B. $m=2016$
|
C. $m=1008$
|
D. $m=2017$
|
Đáp án B
Bài toán 13: Tìm tất cả các giá trị của tham số m
để đồ thị hàm số $y=a{{x}^{4}}+b{{x}^{2}}+c\,\,\,\left( a\ne 0 \right)$ có ba
điểm cực trị tạo thành tam giác cùng điểm O tạo thành hình thoi.
Hướng dẫn giải
${{b}^{2}}=2ac$
Bài 1: Cho
hàm số $y=\frac{1}{4}{{x}^{4}}-\left( m-1 \right){{x}^{2}}+2m+1$ , tìm m để
đồ thị hàm số có 3 điểm cực trị cùng với điểm O tạo thành hình thoi.
Hướng dẫn giải
- Điều
kiện để hàm số có ba điểm cực trị là: $ab<0\Leftrightarrow m>1$
- Áp
dụng công thức ta được: ${{\left( m-1 \right)}^{2}}=2.\frac{1}{4}\left( 2m+1
\right)\Leftrightarrow 2{{m}^{2}}-4m+2=2m+1\Leftrightarrow
m=m=\frac{3+\sqrt{7}}{2}$
Bài 2:
Cho hàm số $y=2{{x}^{4}}+2m{{x}^{2}}-\frac{3m}{2}$, tìm m để đồ thị hàm số có
3 điểm cực trị cùng với điểm O tạo thành hình thoi.

Đáp án D
Bài toán 14: Tìm tất cả các giá trị của tham số m để đồ
thị hàm số $y=a{{x}^{4}}+b{{x}^{2}}+c\,\,\,\left( a\ne 0 \right)$ có ba điểm
cực trị tạo thành tam giác có O là tâm đường tròn nội tiếp.
Hướng dẫn giải
${{b}^{3}}-8a-4abc=0$
Bài 1: Cho
hàm số $y={{x}^{4}}+2m{{x}^{2}}+2m+2$, tìm m để đồ thị hàm số có 3 điểm cực
trị tạo thành tam giác có O là tâm đường tròn nội tiếp.
Hướng dẫn giải
- Điều
kiện để hàm số có 3 điểm cực trị là: $ab<0\Leftrightarrow m<0$
- Áp
dụng công thức ta được: $-8{{m}^{3}}-8-4\left( 2m \right)\left( 2m+2
\right)=0\Leftrightarrow {{m}^{3}}+1+2{{m}^{2}}+2m=0\Leftrightarrow m=-1$
Bài 2:
Cho hàm số $y={{x}^{4}}-2m{{x}^{2}}+2$, tìm m để đồ thị hàm số có 3 điểm cực
trị tạo thành tam giác có O là tâm đường tròn nội tiếp 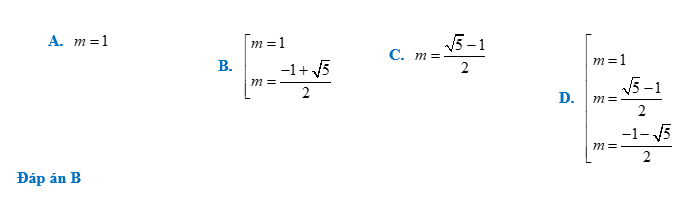
Bài toán 15: Tìm tất cả các giá trị của tham số m để đồ
thị hàm số $y=a{{x}^{4}}+b{{x}^{2}}+c\,\,\,\left( a\ne 0 \right)$ có ba điểm
cực trị tạo thành tam giác nhận O làm tâm đường tròn ngoại tiếp.
Hướng dẫn giải
${{b}^{3}}-8a-8abc=0$
Bài 1: Tìm
tất cả các giá trị của tham số m để đồ thị hàm số $y={{x}^{4}}-4{{x}^{2}}+4m$
có ba điểm cực trị tạo thành tam giác nhận O làm tâm đường tròn ngoại tiếp.
Hướng dẫn giải
- Đồ
thị hàm số luôn có 3 điểm cực trị
- Áp
dụng công thức: $-8-8-8.\left( -4 \right).4m=0\Leftrightarrow m=\frac{1}{8}$
Bài 2: Tìm
tất cả các giá trị của tham số m để đồ thị hàm số $y={{x}^{4}}-2m{{x}^{2}}+m$
có ba điểm cực trị tạo thành tam giác nhận O làm tâm đường tròn ngoại tiếp.
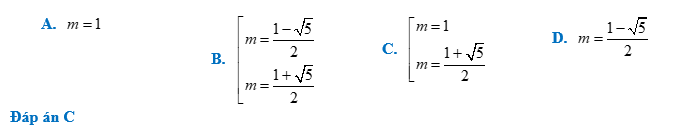
Bài toán 16: Tìm tất cả các giá trị của tham số m để đồ thị
hàm số $y=a{{x}^{4}}+b{{x}^{2}}+c\,\,\,\left( a\ne 0 \right)$ có ba
điểm cực trị tạo thành tam giác có $AB=AC={{n}_{0}}$
Hướng dẫn giải
$16{{a}^{2}}n_{0}^{2}-{{b}^{4}}+8ab=0$
Bài toán 17: Tìm tất cả các giá trị của tham số m để đồ
thị hàm số $y=a{{x}^{4}}+b{{x}^{2}}+c\,\,\,\left( a\ne 0 \right)$ có ba điểm
cực trị tạo thành tam giác có $BC=kAC=kAB$
Hướng dẫn giải
${{b}^{3}}.{{k}^{2}}-8a\left(
{{k}^{2}}-4 \right)=0$
Bài 1: Cho hàm số $y={{x}^{4}}+\left( 3m+1 \right){{x}^{2}}-3$. Tìm tất cả các
giá trị của m để đồ thị hàm số có 3 điểm cực trị tạo thành một tam giác có độ
dài cạnh đáy bằng $\frac{2}{3}$ lần độ dài cạnh bên.
Hướng dẫn giải
- Điều kiện để đồ thị hàm số có 3 điểm cực trị là: $ab<0\Leftrightarrow
3m+1<0\Leftrightarrow m<-\frac{1}{3}$
- Áp dụng công thức có: ${{\left( 3m+1 \right)}^{3}}.\frac{4}{9}-8\left(
\frac{4}{9}-4 \right)=0\Leftrightarrow 4{{\left( 3m+1 \right)}^{3}}=-256\Leftrightarrow
{{\left( 3m+1 \right)}^{3}}=-64\Leftrightarrow m=-\frac{5}{3}$ ( thỏa mãn)
Bài 2: Cho hàm số $y=\frac{1}{4}{{x}^{4}}-2m{{x}^{2}}+2$. Tìm tất cả các
giá trị của m để đồ thị hàm số có 3 điểm cực trị tạo thành một tam giác có độ
dài cạnh đáy bằng 3 lần độ dài cạnh bên.
|
A. $m=-\sqrt[3]{\frac{5}{36}}$
|
B. $m=-\sqrt[3]{\frac{10}{9}}$
|
C. $m=-\sqrt[3]{\frac{1}{4}}$
|
D. $m=-\sqrt[3]{\frac{5}{18}}$
|
Đáp án A
Bài toán 18: Tìm tất cả các giá trị của tham số m để đồ thị
hàm số $y=a{{x}^{4}}+b{{x}^{2}}+c\,\,\,\left( a\ne 0 \right)$ có ba điểm cực
trị tạo thành tam giác sao cho trục hoành chia tam giác ABC thành hai phần có
diện tích bằng nhau.
Hướng dẫn giải
${{b}^{2}}=4\sqrt{2}\left|
ac \right|$
Bài 1: Cho
hàm số tìm m sao cho đồ thị hàm số có ba
điểm cực trị tạo thành tam giác sao cho trục hoành chia tam giác ABC thành
hai phần có diện tích bằng nhau.
Hướng dẫn giải
- Điều
kiện để hàm số có 3 điểm cực trị là: $ab<0\Leftrightarrow
{{m}^{2}}>0\Leftrightarrow m\ne 0$
Áp
dụng công thức ta có 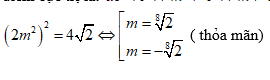
Bài 2:
Cho hàm số $y=2{{x}^{4}}-2{{x}^{2}}+m+2$ tìm m sao cho đồ thị hàm số có ba
điểm cực trị tạo thành tam giác sao cho trục hoành chia tam giác ABC thành
hai phần có diện tích bằng nhau.
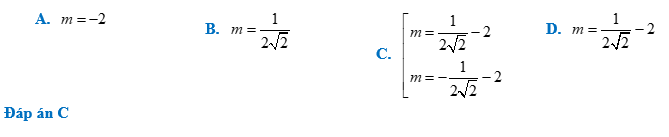
Bài toán 19: Tìm tất cả các giá trị của tham số m để đồ thị
hàm số $y=a{{x}^{4}}+b{{x}^{2}}+c\,\,\,\left( a\ne 0 \right)$ có ba điểm cực
trị tạo thành tam giác có điểm cực trị cách đều trục hoành
Hướng dẫn giải
${{b}^{2}}=8ac$
Bài 1: Tìm
tất cả các giá trị của tham số m để đồ thị hàm số $y={{x}^{4}}+2\left( m-2
\right){{x}^{2}}+{{m}^{2}}-5m+4$ có ba điểm cực trị tạo thành tam giác có
điểm cực trị cách đều trục hoành.
Hướng dẫn giải
- Điều
kiện để hàm số đã cho có 3 điểm cực trị là: $ab<0\Leftrightarrow m<2$
- Áp
dụng công thức ta được: $4{{\left( m-2 \right)}^{2}}=8\left( {{m}^{2}}-5m+4
\right)\Leftrightarrow {{m}^{2}}-4m+4=2{{m}^{2}}-10m+8\Leftrightarrow
m=3-\sqrt{5}$
Bài 2: Tìm
tất cả các giá trị của tham số m để đồ thị hàm số
$y=-{{x}^{4}}-2m{{x}^{2}}+{{m}^{2}}+m$ có ba điểm cực trị tạo thành tam giác
có điểm cực trị cách đều trục hoành.
|
A. $m=0$
|
B. $m=-\frac{2}{3}$
|
C. $m=-1$
|
D. $m=1$
|
Đáp án B
Bài toán 20: Tìm tất cả các giá trị của tham số m để đồ thị
hàm số $y=a{{x}^{4}}+b{{x}^{2}}+c\,\,\,\left( a\ne 0 \right)$ để đồ thị hàm
số cắt Ox tại 4 điểm phân biệt có hoành độ lập thành cấp số cộng.
Hướng dẫn giải
${{b}^{2}}=\frac{100}{9}ac$
Bài 1:
Cho hàm số $y={{x}^{4}}+2m{{x}^{2}}+{{m}^{2}}+m$ , tìm m để đồ thị hàm số cắt
trục hoành tại 4 điểm phân biệt có hoành độ lập thành cấp số cộng.
Hướng dẫn giải
- Điều
kiện để hàm số có 3 điểm cực trị là: $ab<0\Leftrightarrow m<0$
- Áp
dụng công thức ta được: ${{\left( 2m \right)}^{2}}=\frac{100}{9}\left(
{{m}^{2}}+m \right)\Leftrightarrow m=-\frac{25}{16}$
Bài 2: Cho
hàm số , tìm m để đồ thị hàm số cắt trục hoành tại 4 điểm phân
biệt có hoành độ lập thành cấp số cộng.
|
A. $m=-1$
|
B. $m=0$
|
C. $m=\frac{16-5\sqrt{34}}{9}$
|
D. $m=\frac{16+5\sqrt{34}}{9}$
|
Đáp án D
Bài toán 21: Tìm tất cả các giá trị của tham số m để hình
phẳng giới hạn bởi đồ thị hàm
số $y=a{{x}^{4}}+b{{x}^{2}}+c\,\,\,\left( a\ne 0 \right)$ và trục
hoành có diện tích phần trên và phần dưới bằng nhau.
Hướng dẫn giải
${{b}^{2}}=\frac{36}{5}ac$
Bài 1: Cho
hàm số $y={{x}^{4}}-2\left( m+1 \right){{x}^{2}}+5$ , tìm m để hình phẳng
giới hạn bởi đồ thị hàm số đã cho và trục hoành có diện tích phần trên và
phần dưới bằng nhau.
Hướng dẫn giải
Áp
dụng công thức ta được:
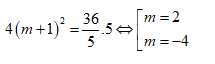
Bài 2: Cho
hàm số $y={{x}^{4}}+2\left( m-2 \right){{x}^{2}}+20$ , tìm m để hình phẳng
giới hạn bởi đồ thị hàm số đã cho và trục hoành có diện tích phần trên và
phần dưới bằng nhau.

Bài toán 22: Phương trình đường tròn ngoại tiếp tam giác
ABC: ${{x}^{2}}+{{y}^{2}}-\left( \frac{2}{b}-\frac{\Delta }{4a}+c
\right)y+c\left( \frac{2}{b}-\frac{\Delta }{4a} \right)=0,\Delta
={{b}^{2}}-4ac$
|