Chuyên đề các bài toán liên quan đến đường thẳng đi qua các điểm cực trị của hàm số

Bài 1: (THPT chuyên ĐHSP Hà Nội lần 2) Giá trị m để hàm số $y=\frac{\cot x-2}{\cot x-m}$ nghịch biến trên $\left( \frac{\pi }{4};\frac{\pi }{2} \right)$ là:

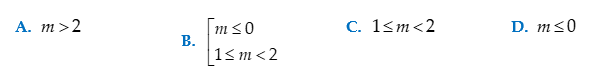
Hướng dẫn giải

Chọn B

Đặt $t=\cot x$

Có $x\in \left( \frac{\pi }{4};\frac{\pi }{2} \right)\Rightarrow t\in \left( 0;1 \right)$

Ta có hàm số $t=\cot x$ nghịch biến trên $\left( \frac{\pi }{4};\frac{\pi }{2} \right)$ nên x tăng trên $\left( \frac{\pi }{4};\frac{\pi }{2} \right)$ thì t giảm trên $\left( 0;1 \right)$

Suy ra đề bài trở thành tìm m để hàm số $f\left( t \right)=\frac{t-2}{t-m}$ đồng biến trên $\left( 0;1 \right)$

Xét hàm số $f\left( t \right)=\frac{t-2}{t-m}$ trên $\left( 0;1 \right)$

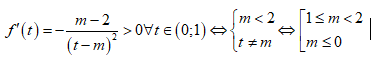
Bài 2: (THPT chuyên Hạ Long- 2017) Tìm các giá trị thức của tham số m để hàm số $y=\frac{m-\operatorname{sinx}}{{{\cos }^{2}}x}$ nghịch biến trên khoảng $\left( 0;\frac{\pi }{6} \right)$

Đáp án D

Bài 3: (THPT Yên Lạc-Vĩnh Phúc) Cho hàm số $y=\frac{\left( m-1 \right)\sqrt{x-1}+2}{\sqrt{x-1}+m}$ . Tìm tất cả các giá trị của tham số m để hàm số đồng biến trên khoảng $\left( 17;37 \right)$

Bài 1: (THPT chuyên Bắc Ninh lần 1-2018)Đồ thị hàm số $y={{x}^{3}}-3{{x}^{2}}-9x+1$ có hai điểm cực trị A và B. Điểm nào dưới đây thuộc đường thẳng AB?

Hướng dẫn giải

Chọn A

Áp dụng công thức ta có: Đường thẳng đi qua hai điểm A và B là:

$y=\left( \frac{2.\left( -9 \right)}{3}-\frac{2.{{\left( -3 \right)}^{2}}}{9.1} \right)x+1-\frac{\left( -3 \right).\left( -9 \right)}{9.1}=-8x-2$

Vậy điểm $M\left( 1;-10 \right)$ thuộc đường thẳng AB

Bài 2: (THPT Xuân Hòa Lần 1-2018) Biết đồ thị hàm số $y={{x}^{3}}-3x+1$ có hai điểm cực trị A, B. Khi đó phương trình đường thẳng AB là:

Đáp án A

Bài 3: (THPT Quang Trung- Bình Định-2017) Cho hàm số $y={{x}^{3}}+3\left( m-1 \right){{x}^{2}}+3\left( m-1 \right)x+1$. Với giá trị nào sau đây của tham số m thì hàm số có hai cực trị và đường thẳng nối hai điểm cực trị đi qua $M\left( 0;-3 \right)$

Đáp án B

Bài toán 2: Hàm số bậc 3 $y=a{{x}^{3}}+b{{x}^{2}}+cx+d\,\,\left( a\ne 0 \right)$ có điểm cực đại và cực tiểu đối xứng với nhau qua đường thẳng d: $y=kx+m$

Hướng dẫn giải

-          Khi đó có điểm uốn chính là tâm đối xứng, nên có:

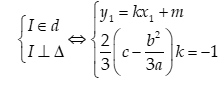với $I\left( {{x}_{1}};{{y}_{1}} \right)$ là điểm uốn của đồ thị. ${{x}_{1}}$ là nghiệm của phương trình $y''=0$

Bài 1: Xác định tất cả các giá trị của m để hai điểm cực trị của đồ thị hàm số $y={{x}^{3}}-3{{x}^{2}}+mx$ đối xứng với nhau qua đường thẳng $x-2y-5=0$

Hướng dẫn giải

Chọn A

Ta có: $y'=3{{x}^{2}}-6x;y''=6x-6=0\Leftrightarrow x=1$

Vậy điểm uốn $I\left( 1;m-2 \right)$

Áp dụng công thức ta được:

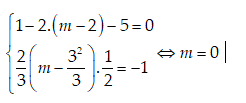
Bài 2: Xác định tất cả các giá trị của m để hai điểm cực trị của đồ thị hàm số $y={{x}^{3}}-3m{{x}^{2}}+4{{m}^{3}}$ đối xứng với nhau qua đường thẳng $d:y=x$

Đáp án B

Bài 3: Xác định tất cả các giá trị của m để hai điểm cực trị của đồ thị hàm số $y={{x}^{3}}-3\left( m+1 \right){{x}^{2}}+9x+m-2$ đối xứng với nhau qua đường thẳng $d:y=\frac{1}{2}x$

Đáp án C

Bài 4: Xác định tất cả các giá trị của m để hai điểm cực trị của đồ thị hàm số $y={{x}^{3}}+3m{{x}^{2}}-3m-1$ đối xứng với nhau qua đường thẳng $d:x+8y-74=0$

Đáp án A

Bài toán 3: Đường thẳng đi qua điểm cực trị của hàm phân thức $f\left( x \right)=\frac{u\left( x \right)}{v\left( x \right)}$ có dạng là:

$d:y=\frac{u'\left( x \right)}{v'\left( x \right)}$

Bài 1: ( chuyên KHTN Hà Nội) Cho hàm số $y=\frac{m{{x}^{2}}-2x+m-1}{2x+1}$ . Đường thẳng nối hai điểm cực trị của đồ thị hàm số này vuông góc với đường phân giác của góc phần tư thứ nhất khi m bằng?

Hướng dẫn giải

Chọn C

Đường thẳng phân giác của góc phần tư thứ nhất là $y=x$

Đường thẳng nối hai điểm cực trị của hàm số là $y=mx-1$

Điều kiện thỏa mãn bài toán khi và chỉ khi $1.m=-1\Rightarrow m=-1$ 

Bài viết gợi ý: