BÀI TẬP NÂNG CAO RÈN LUYỆN KỸ NĂNG OXYZ
Câu 1: Trong không
gian cho mặt phẳng (P) đi qua M(2;3;5) và cắt các tia Ox, Oy, Oz lần lượt tại
A, B, C sao cho giá trị của OA, OB, Oc theo thứ tự lập thành cấp số nhân có
công bội bằng 3. Khi đó khoảng cách từ O đến (P) là:
A.$\frac{18}{\sqrt{91}}$
B.$\frac{24}{\sqrt{91}}$
C.$\frac{16}{\sqrt{91}}$
D.$\frac{32}{\sqrt{91}}$
HD: Theo giả
thuyết ta có: (P): $\frac{2}{a}+\frac{3}{b}+\frac{5}{b}=1$
Do a, b, c
thứ tự là một cấp số nhân có công bội là 3 => 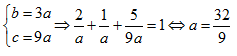
$\Rightarrow d\left[ I;\left( P \right) \right]=\frac{32}{\sqrt{91}}$ => D
Câu 2: Trong không gian cho điểm M(1;2;3), gọi (P): px + qy + rz =1 là mặt phẳng qua M và cắt các trục tọa độ Ox, Oy, Oz tại A, B, C sao cho M là trong tâm tam giác ABC. Tính T = p + q + r
A.$-\frac{11}{18}$
B.$18$
C.$\frac{11}{18}$
D.$-18$ $$
HD: Do (P) cắt
các trục tọa độ Ox; Oy; Oz tại A, B, C => A(a;0;0), B(0;b;0), C(0;0;c) với
abc ≠
0
=> 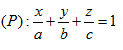
Do M là trọng tâm tam giác ABC => 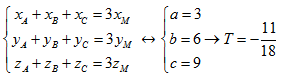
=>A
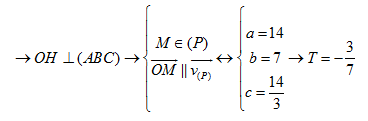
Câu 3: Trong không gian cho điểm M(1;2;3), gọi (P): px + qy + rz =1 $(p,q,r\in R)$ là mặt phẳng qua M và cắt các trục tọa độ Ox, Oy, Oz tại A, B, C sao cho M là trực tâm tam giác ABC. Tính T = p + q + r
A.$\frac{77}{3}$
B.$\frac{3}{7}$
C.$-\frac{77}{3}$
D.$-\frac{3}{7}$
HD: HD: Do
(P) cắt các trục tọa độ Ox; Oy; Oz tại A, B, C => A(a;0;0), B(0;b;0),
C(0;0;c) với abc ≠0
=>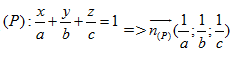
Ta có OABC là một tứ diện vuống tại O có H là trực tâm
tam giác ABC => $AH\bot BC$
Mặt khác: $OA\bot BC(OA\bot (OBC))$
Vậy $BC\bot (OAH)\to BC\bot OH$ , tương tự ta có $AB\bot
OH$
Câu 4: Trong không
gian cho $\left| \overrightarrow{a} \right|=3$ ;$\left| \overrightarrow{b}
\right|=2$ ;$\left( \overrightarrow{a},\overrightarrow{b} \right)={{120}^{0}}$ .
Gọi 2 vecto \[\overrightarrow{p}=2\overrightarrow{a}-\overrightarrow{b}\] ;\[\overrightarrow{q}=\overrightarrow{a}+2\overrightarrow{b}\]
. Tính $\cos \left( \overrightarrow{p},\overrightarrow{q} \right)$
A.$\frac{1}{4\sqrt{39}}$
B.$\frac{1}{\sqrt{39}}$
C.$\frac{1}{2\sqrt{39}}$
D.$\frac{1}{3\sqrt{39}}$
HD: Ta có $\overrightarrow{p}.\overrightarrow{q}=(2\overrightarrow{a}-\overrightarrow{b})(\overrightarrow{a}+2\overrightarrow{b})=2{{\left| \overrightarrow{a} \right|}^{2}}+3\overrightarrow{a}\overrightarrow{b}-2{{\left| \overrightarrow{b} \right|}^{2}}={{2.3}^{2}}+3.3.2.cos{{120}^{o}}-{{2.2}^{2}}=1$
${{\left| \overrightarrow{p} \right|}^{2}}=4{{\left|
\overrightarrow{a} \right|}^{2}}-4\overrightarrow{a}\overrightarrow{b}+{{\left|
\overrightarrow{b} \right|}^{2}}={{4.3}^{2}}-4.3.2.\cos
{{120}^{o}}+{{2}^{2}}=48$
${{\left| \overrightarrow{q} \right|}^{2}}={{\left|
\overrightarrow{a}
\right|}^{2}}+4\overrightarrow{a}\overrightarrow{b}+4{{\left|
\overrightarrow{b} \right|}^{2}}={{3}^{2}}+4.3.2.\cos
{{120}^{o}}+{{4.2}^{2}}=13$
$\to \cos (\overrightarrow{p},\overrightarrow{q})=\frac{\overrightarrow{p}.\overrightarrow{q}}{\left| \overrightarrow{p} \right|.\left| \overrightarrow{q} \right|}=\frac{1}{4\sqrt{39}}\Rightarrow A$
Câu 5: Trong không
gian cho mặt phẳng (P): x + 2y + 3z + 4 = 0 và hai điểm M, N là 2 điểm đối xứng
nhau qua (P), M thuộc mặt cầu (C): ${{x}^{2}}+{{(y+4)}^{2}}+{{z}^{2}}=5$ . Hỏi
N thuộc mặt cầu nào sau đây:
A.${{x}^{2}}+{{y}^{2}}+{{z}^{2}}-\frac{8}{7}x+\frac{40}{7}y-\frac{24}{7}z+\frac{45}{7}=0$
B.${{x}^{2}}+{{y}^{2}}+{{z}^{2}}-\frac{8}{7}x-\frac{40}{7}y-\frac{24}{7}z+\frac{45}{7}=0$
C.${{x}^{2}}+{{y}^{2}}+{{z}^{2}}+\frac{8}{7}x+\frac{40}{7}y+\frac{24}{7}z+\frac{45}{7}=0$
D.${{x}^{2}}+{{y}^{2}}+{{z}^{2}}-\frac{8}{7}x-\frac{40}{7}y-\frac{24}{7}z+\frac{45}{7}=0$
HD: Gọi I là tâm của mặt cầu (C) => I(0;-4;0)
Gọi I’ đối xứng I qua (P) => $I'(\frac{4}{7};-\frac{20}{7};\frac{12}{7})$
Theo yêu cầu bài toán ta có:
$M\in (C)$ có tâm $I(0;-4;0)$ và bán kính $R=\sqrt{5}\Rightarrow N\in (S)$ có tâm $I'(\frac{4}{7};-\frac{20}{7};\frac{12}{7})$ bán kính $R=\sqrt{5}$ $\Rightarrow (S):{{x}^{2}}+{{y}^{2}}+{{z}^{2}}-\frac{8}{7}x-\frac{24}{7}y+\frac{45}{7}z=0$ => A
Câu 6: Trong không
gian cho mặt phẳng (P): x – y + z + 1 = 0, A(1;1;1), B(0;1;2), C(-2;0;1) và
M(a;b;c) sao cho $S=2M{{A}^{2}}+M{{B}^{2}}+M{{C}^{2}}$ đạt giá trị nhỏ nhất.
Tính T = 3a + 2b + c
A.$\frac{25}{4}$
B.$\frac{25}{2}$
C.$-\frac{25}{4}$
D.$-\frac{25}{2}$
HD: Gọi I là điểm thõa mãn $2\overrightarrow{IA}+\overrightarrow{IB}+\overrightarrow{IC}=\overrightarrow{0}\Rightarrow I(0;\frac{3}{4};\frac{5}{4})$
Ta có: $S=2M{{A}^{2}}+M{{B}^{2}}+M{{C}^{2}}=2{{(\overrightarrow{MI}+\overrightarrow{IA})}^{2}}+{{(\overrightarrow{MI}+\overrightarrow{IB})}^{2}}+{{(\overrightarrow{MI}+\overrightarrow{IC})}^{2}}$
$=4M{{I}^{2}}+2I{{A}^{2}}+I{{B}^{2}}+2\overrightarrow{MI}(2\overrightarrow{IA}+\overrightarrow{IB}+\overrightarrow{IC})$
$=4M{{I}^{2}}+2I{{A}^{2}}+I{{B}^{2}}+I{{C}^{2}}$
Do $2I{{A}^{2}}+I{{B}^{2}}+I{{C}^{2}}$ là hằng số nên ${{S}_{\min
}}\Leftrightarrow $ M là hình chiếu của I trên (P)
$\Rightarrow M(-\frac{3}{2};-\frac{3}{4};-\frac{1}{4})\Rightarrow T=-\frac{25}{4}$ => C
Câu 7: Trong không
gian cho 2 điểm A(1;0;2) và B(3;1;-1) và mặt phẳng (P): x + y + z - 1 = 0. Gọi
điểm $M({{x}_{0}};{{y}_{0}};{{z}_{0}})$ sao cho \[\left|
3\overrightarrow{MA}-2\overrightarrow{MB} \right|\] đạt giá trị nhỏ nhất. Tính $A=9{{x}_{0}}+3{{y}_{0}}+6{{z}_{0}}$
A.2
B.1
C.3
D.4
HD: Gọi I là điểm thõa mãn \[3\overrightarrow{IA}-2\overrightarrow{IB}=\overrightarrow{0}=>I(-3;-2;8)\]
Ta có $\left| 3\overrightarrow{MA}-2\overrightarrow{MB}
\right|=\left|
3(\overrightarrow{IA}-\overrightarrow{IM})-2(\overrightarrow{IB}-\overrightarrow{IM})
\right|=\left| 3\overrightarrow{IA}-2\overrightarrow{IB}-\overrightarrow{IM}
\right|=\left| \overrightarrow{IM} \right|=IM$
Vì I cố định, $M\in (P)$ nên $\left|
3\overrightarrow{MA}-2\overrightarrow{MB} \right|$ đạt giá trị nhỏ nhất $\Leftrightarrow IM$ đạt giá trị nhỏ nhất
$\Leftrightarrow M$ là hình chiếu của I trên (P)
Gọi (d) là đường thẳng qua I và vuông góc với mặt (P) $\Rightarrow
\overrightarrow{{{n}_{(d)}}}=\overrightarrow{{{n}_{(P)}}}=(1;1;1)$
$\Rightarrow (d):x=-3+t.y=-2+t.z=8+t$
$M=(d)\cap (P)\Rightarrow M(-\frac{11}{3};-\frac{8}{3};\frac{22}{3})$=>A=3
Câu 8: Trong không
gian cho mặt phẳng (P): x + 2y + 2z + 7 = 0 và ba điểm A(1;2;-1), B(3;1;-2),
C(1;-2;1). Điểm $M(a;b;c)\in (P)$ sao cho $M{{A}^{2}}-M{{B}^{2}}-M{{C}^{2}}$ đạt
giá trị lớn nhất. Khi đó tổng A=a + b+ c bằng bao nhiêu
A.$\frac{20}{9}$
B.$\frac{14}{9}$
C.$-\frac{20}{9}$
D.$-\frac{14}{9}$
HD: Ta có 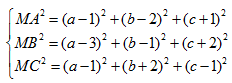
$\Rightarrow
M{{A}^{2}}-M{{B}^{2}}-M{{C}^{2}}=-{{a}^{2}}+6a-{{b}^{2}}-6b-{{c}^{2}}+26=44-\left[
{{(a-3)}^{2}}+{{(b+3)}^{2}}+{{c}^{2}} \right]$
Vậy ${{(M{{A}^{2}}-M{{B}^{2}}-M{{C}^{2}})}_{\max
}}\Leftrightarrow {{\left[ {{(a-3)}^{2}}+{{(b+3)}^{2}}+{{c}^{2}} \right]}_{\max
}}\Leftrightarrow M{{I}_{\min }}$ với $I(3;-3;0)$
Mà $I$ cố định nên $M{{I}_{\min }}$ khi M là hình chiếu
I trên (P)
Gọi (d) là đường thẳng qua I là vuông với với (P), ta
có:
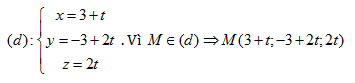
$M\in
(P)\Rightarrow (3+t)+2(-3+2t)+2.2t+7=0\Rightarrow t=-\frac{4}{9}\Rightarrow
M(\frac{23}{9};-\frac{35}{9};-\frac{8}{9})$
$\Rightarrow a+b+c=-\frac{20}{9}$ => C
Câu 9: Trong không
gian cho ba điểm A(1;1;0(, B(0;1;1), C(1;0;1). Tìm tập hợp tất cả các điểm M
trên (Oxz) sao cho $\overrightarrow{MA}.\overrightarrow{MB}+{{\overrightarrow{MC}}^{2}}=2$
A.Một đường thẳng
B.Một đường tròn
C.Một đường elip
D.Không xác định được
$\overrightarrow{AB}(-1;0;1)\Rightarrow AB=\sqrt{2}$
Gọi I là
trung điểm AB $\Rightarrow I(\frac{1}{2};1;\frac{1}{2})$ cố định và $I{{C}^{2}}=\frac{3}{2}$
Ta có: $\overrightarrow{MA}.\overrightarrow{MB}=(\overrightarrow{IA}-\overrightarrow{IM}).(\overrightarrow{IB}-\overrightarrow{IM})=-I{{A}^{2}}-\overrightarrow{IM}(\overrightarrow{IA}+\overrightarrow{IB})+I{{M}^{2}}=-\frac{1}{2}+I{{M}^{2}}$
Vậy $\overrightarrow{MA}.\overrightarrow{MB}+{{\overrightarrow{MC}}^{2}}=2\Leftrightarrow
M{{I}^{2}}+M{{C}^{2}}=\frac{5}{2}$
Gọi J là
trung điểm của IC $\Rightarrow J(\frac{3}{4};\frac{1}{2};\frac{3}{4})$ cố định và MJ là đường trung tuyến tam giác
MIC
$\Rightarrow
\frac{5}{2}=M{{I}^{2}}+M{{C}^{2}}=2M{{J}^{2}}+\frac{I{{C}^{2}}}{2}=2J{{M}^{2}}+\frac{3}{4}\Rightarrow
I{{M}^{2}}=\frac{7}{8}\Rightarrow IM=\frac{\sqrt{14}}{4}$
Mà J cố định
nên M di động trên mặt cầu (S) tâm J với bán kính $R=\frac{\sqrt{14}}{4}$
Mặt phẳng
Oxz có phương trình y=0 $\Rightarrow d\left[ J,(Oxz)
\right]=\frac{1}{2}<\frac{\sqrt{14}}{4}=R\Rightarrow (S)\cap (Oxz)$ là một
đường tròn $(C)$ => B







