PHƯƠNG PHÁP GIẢI HÌNH HỌC
TỌA ĐỘ TRONG KHÔNG GIAN
A/Lý thuyết
I/Tích có hướng của 2 vecto
1.Định nghĩa
Trong hệ trục
Oxyz, cho hai vecto $\overrightarrow{u}(a;b;c)$ và $\overrightarrow{v}(a';b';c')$
khi đó tích có hướng của $\overrightarrow{u}$ và $\overrightarrow{v}$ được xác
định như sau
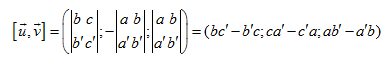
2.Tính chất
a. $\overrightarrow{u}\bot
\overrightarrow{v}\Leftrightarrow \overrightarrow{u}.\overrightarrow{v}=0$
b. $\overrightarrow{u}$
và$\overrightarrow{v}$ cùng phương $\Leftrightarrow \left[ \overrightarrow{u},\overrightarrow{v}
\right]=0$
c. $\overrightarrow{u},\overrightarrow{v},\overrightarrow{\text{w}}$
đồng phẳng $\Leftrightarrow \left[ \overrightarrow{u},\overrightarrow{v}
\right].\overrightarrow{\text{w}}=0$
II/ Các phương trình
1.Phương trình mặt phẳng:
Mặt phẳng
(P) đi qua điểm ${{M}_{0}}({{x}_{0}};{{y}_{0}};{{z}_{0}})$ với vecto pháp tuyến
$\overrightarrow{n}(A;B;C)$ có phương trình:
$A(x-{{x}_{0}})+B(y-{{y}_{0}})+C(z-{{z}_{0}})=0$
2.Phương trình đường thẳng:
Cho đường thẳng
d đi qua điểm ${{M}_{0}}({{x}_{0}};{{y}_{0}};{{z}_{0}})$ và có vecto chỉ phương
$\overrightarrow{u}(a;b;c)$ . Khi đó:
+Phương
trình tham số của d là: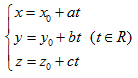 
+Phương
trình chính tắc của d là: $\frac{x-{{x}_{0}}}{a}=\frac{y-{{y}_{0}}}{b}=\frac{z-{{z}_{0}}}{c}$
$(abc\ne 0)$
3/Phương trình mặt cầu
Mặt cầu tâm $I({{x}_{0}};{{y}_{0}};{{z}_{0}})$
bán kính R có phương trình
${{(x-{{x}_{0}})}^{2}}+{{(y-{{y}_{0}})}^{2}}+(z-{{z}_{0}})={{R}^{2}}$
Hoặc
${{x}^{2}}+{{y}^{2}}+{{z}^{2}}-2ax-2by-2cz+d=0$
có tâm $(a;b;c)$ bán kính $R=\sqrt{{{a}^{2}}+{{b}^{2}}+{{c}^{2}}-d}$
III/Vị trí tương đối của 2 đường thẳng
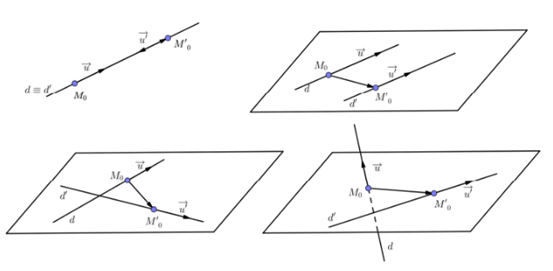
+ $\left[
\overrightarrow{u},\overrightarrow{u'} \right]=\overrightarrow{0}$ : d và d’
song song hoặc trùng nhau
-
${{M}_{0}}\in
d'$ : d và d’ trùng nhau
-
${{M}_{0}}\notin
d'$ : d và d’ song song
+ $\left[
\overrightarrow{u},\overrightarrow{u'} \right]\ne 0$ : d và d’ cắt nhau hoặc
chéo nhau
-
$\left[
\overrightarrow{u},\overrightarrow{u'} \right].\overrightarrow{M{{M}_{0}}}=0$ :
d và d’ cắt nhau
-
$\left[
\overrightarrow{u},\overrightarrow{u'} \right].\overrightarrow{M{{M}_{0}}}\ne
0$ : d và d’ chéo nhau
2. Vị trí tương đối của hai mặt phẳng
IV/Khoảng cách
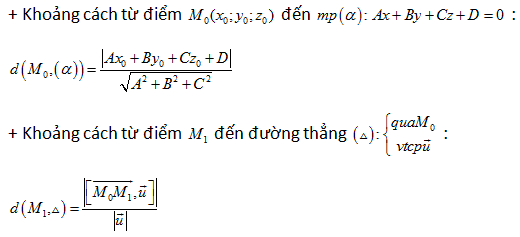
+ Khoảng
cách giữa 2 đường thẳng chéo nhau
$d\left(
\vartriangle ,\vartriangle ' \right)=\frac{\left| \left[
\overrightarrow{u},\overrightarrow{u'}
\right].\overrightarrow{{{M}_{0}}{{M}_{0}}'} \right|}{\left| \left[
\overrightarrow{u},\overrightarrow{u'} \right] \right|}$
V/ Các công thức liên quan
+ Diện tích hình
bình hành: ${{S}_{ABCD}}=\left| \left[ \overrightarrow{AB},\overrightarrow{AD}
\right] \right|$
+ Diện tích
tam giác: ${{S}_{ABC}}=\frac{\left| \left[
\overrightarrow{AB};\overrightarrow{AC} \right] \right|}{2}$
+ Thể tích
hình hộp: ${{V}_{ABCD.A'B'C'D'}}=\left| \left[
\overrightarrow{AB},\overrightarrow{AD} \right].\overrightarrow{AA'} \right|$
+ Thể tích tứ
diện: ${{S}_{ABCD}}=\frac{\left| \left[ \overrightarrow{AB};\overrightarrow{AC}
\right].\overrightarrow{AD} \right|}{6}$
B/Ví dụ
Câu 1: Trong không gian cho điểm $A(2;2;1)$
. Tính độ dài đoạn OA
A.3
B.9
C.7
D.5
HD: $OA=\sqrt{{{2}^{2}}+{{2}^{2}}+{{1}^{2}}}=3$
=> A
Câu 2: Trong không gian
cho hai vecto $\overrightarrow{a}(2;1;0)$ và $\overrightarrow{b}(-1;0;-2)$ .
Tính $\cos (\overrightarrow{a},\overrightarrow{b})$
A.$\cos (\overrightarrow{a},\overrightarrow{b})=\frac{2}{25}$
B.$\cos (\overrightarrow{a},\overrightarrow{b})=-\frac{2}{5}$
C.$\cos (\overrightarrow{a},\overrightarrow{b})=-\frac{2}{25}$
D.$\cos (\overrightarrow{a},\overrightarrow{b})=\frac{2}{5}$
HD:
\[\cos
(\overrightarrow{a},\overrightarrow{b})=\frac{2.(-1)+1.0+0.(-2)}{\sqrt{{{2}^{2}}+{{1}^{2}}+{{0}^{2}}}.\sqrt{{{(-1)}^{2}}+{{0}^{2}}+{{(-2)}^{2}}}}=-\frac{2}{5}\]
=> B
Câu 3: Trong không gian
cho ba điểm $M(2;3;-1);N(-1;1;1);P(1;m-1;2)$ . Tìm m để tam giác MNP vuông tại
N
A.-6
B.0
C.-4
D.2
HD: Ta có: $\overrightarrow{MN}(-3;-2;2);\overrightarrow{NP}(2;m-2;1)$
Tam giác MNP vuông tại N ↔ $\overrightarrow{MN}.\overrightarrow{NP}=\overrightarrow{0}$
khi và chỉ khi$-3.2+(-2).(m-2)+2.1=0\leftrightarrow
-2(m-2)=4\leftrightarrow m-2=-2\leftrightarrow m=0$
=> B
Câu 4: Trong không gian
cho điểm $A(1;2;3)$ , trên trục Oz lấy điểm M sao cho $AM=\sqrt{5}$ . Tìm tọa độ
điểm M
A.(0;0;3)
B.(0;0;2)
C.(0;0;-3)
D.(0;3;0)
HD: Gọi điểm M(0;0;z) $\in$ Oz →
$AM=\sqrt{{{1}^{2}}+{{2}^{2}}+{{(z-3)}^{2}}}$ ; $AM=\sqrt{5}$ $\leftrightarrow
\sqrt{{{1}^{2}}+{{2}^{2}}+{{(z-3)}^{2}}}=\sqrt{5}$ ↔ z – 3 =0 ↔ z = 3 => A
Câu 5: Trong không gian
cho tứ diện ABCD có tọa độ các đỉnh $A(5;3;-1);B(2;3;-4);C(1;2;0);D(3;1;-2)$ .
Thể tích khối tứ diện đã cho là
A.3
B.$\frac{9}{2}$
C.4
D.$\frac{7}{2}$
HD: $\overrightarrow{AB}(-3;0;-3)$
; $\overrightarrow{AC}(-4;-1;1)$ ; $\overrightarrow{AD}(-2;-2;-1)$
$V=\frac{\left|
\left[ \overrightarrow{AB};\overrightarrow{AC} \right].\overrightarrow{AD}
\right|}{6}=\frac{9}{2}$ => B
C/ Bài tập tự luyện
Câu 1: Trong không gian cho hai điểm $A(4;0;1);B(-2;2;3)$
. Phương trình trung trực của đoạn thẳng AB là:
A.$3x-y-z=0$
B.$3x+y+z-6=0$
C.$3x-y-z+1=0$
D.$6x-2y-2z-1=0$
Câu 2: Trong không gian cho mặt phẳng x+y+z-6=0 . Điểm nào sau
đây không thuộc mặt phẳng đã cho?
A.N(2;2;2)
B.Q(3;3;0)
C.P(1;2;3)
D.M(1;-1;1)
Câu 3: Trong không gian cho điểm $M(3;-1;-2)$
và mặt phẳng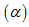 
:3x-y+2z+4=0 . Phương trình mặt phẳng qua M và song song với 
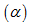là
A.$3x+y-2z-14=0$
B.$3x-y+2z+6=0$
C.$3x-y+2z-6=0$
D.$3x-y-2z+6=0$
Câu 4: Trong không gian cho điểm $M(1;2;3)$ .
Gọi ${{M}_{1}};{{M}_{2}}$ lần lượt là hình chiếu vuông góc của M lên Ox, Oy.
Vecto nào sau đây là vecto chỉ phương của đường thẳng ${{M}_{1}}{{M}_{2}}$ ?
A.(1;2;0)
B.(1;0;0)
C.(-1;2;0)
D.(0;2;0)
Câu 5: Trong không gian cho mặt phẳng $(P):2x+y+z+5=0$ và đường thẳng $(d):\frac{x-1}{3}=\frac{y-3}{-1}=\frac{z-2}{3}$
. Tìm tọa độ giao điểm của (d) và (P)?
A.(17;9;20)
B.(17;-9;-20)
C.(-17;0;20)
D.(1;3;2)
|
1 |
2 |
3 |
4 |
5 |
|
C |
D |
A |
C |
C |
