Bài Tập Con Lắc Đơn

BÀI TẬP CON LẮC ĐƠN

Câu 1: (Minh họa – 2017) Một con lắc đơn có chiều dài 1 m, được treo tại nơi có gia tốc trọng trường g = π² m/s². Giữ vật nhỏ của con lắc ở vị trí có li độ góc −9^o rồi thả nhẹ vào lúc t = 0. Phương trình dao động của vật là

A. \[s=5\cos \left( \pi t+\pi \right)\]cm B. \[s=5\cos \left( 2\pi t \right)\]cm

C. \[s=5\pi \cos \left( \pi t+\pi \right)\]cm D. \[s=5\pi \cos \left( 2\pi t \right)\]cm

Hướng dẫn

Tần số góc của dao động \[\omega =\sqrt{\frac{g}{l}}=\sqrt{\frac{{{\pi }^{2}}}{1}}=\pi \]rad/s

Biên độ cong của dao động \[{{s}_{0}}=l{{\alpha }_{0}}=1\frac{{{9}^{0}}}{{{180}^{0}}}\pi =5\pi cm\]

Ban đầu vật ở vị trí biên âm, do vậy phương trình dao động sẽ là \[s=5\pi \cos \left( \pi t+\pi \right)\]cm

Đáp án C

Câu 2: (Quốc gia – 2010) Tại nơi có gia tốc trọng trường g, một con lắc đơn dao động điều hòa với biên độ góc a₀ nhỏ. Lấy mốc thế năng ở vị trí cân bằng. Khi con lắc chuyển động nhanh dần theo chiều dương đến vị trí có động năng bằng thế năng thì li độ góc a của con lắc bằng

A. \[\frac{{{\alpha }_{0}}}{\sqrt{3}}\] B. \[\frac{{{\alpha }_{0}}}{\sqrt{2}}\] C. \[-\frac{{{\alpha }_{0}}}{\sqrt{2}}\] D. \[-\frac{{{\alpha }_{0}}}{\sqrt{3}}\]

Hướng dẫn

Động năng bằng thế năng tại vị trí \[\alpha =\pm \frac{{{\alpha }_{0}}}{\sqrt{2}}\], vật chuyển động theo chiều dương \[\Rightarrow \alpha =-\frac{{{\alpha }_{0}}}{\sqrt{2}}\]

Đáp án C

Câu 3: Một con lắc đơn có chiều dài dây treo l = 2m dao động điều hòa trọng trường biên độ góc \[{{\alpha }_{0}}=0,175\] rad . Chọn mốc thế năng của vật tại vị trí cân bằng. Ở vị trí tại đó vật có động năng bằng ba lần thế năng thì chiều dài cung tính từ vị trí cân bằng đến vị trí của vật gần bằng

A. 22,5 cm B. 30,0 cm C. 17,5 cm D. 25,0 cm

Hướng dẫn

Động năng bằng ba lần thế năng tại vị trí \[\alpha =\pm \frac{{{\alpha }_{0}}}{2}\]

Độ dài cung tương ứng \[s=l\alpha =2\frac{0,175}{2}=17,5cm\]

Đáp án C

Câu 4: Một con lắc đơn dao động điều hòa với phương trình dao động \[s=7,2\cos \left( \frac{5\pi }{6}t-\frac{\pi }{3} \right)cm\]. Lấy \[g={{\pi }^{2}}\]cm/s². Biên độ góc của dao động

A. 0,069 rad B. 0,072 rad C. 0,05 rad D. 0,036 rad

Hướng dẫn

Ta có \[\omega =\sqrt{\frac{g}{l}}\Leftrightarrow \frac{5\pi }{6}=\sqrt{\frac{{{\pi }^{2}}}{l}}\Rightarrow l=1,44m\]

Biên độ góc của dao động \[{{\alpha }_{0}}=\frac{{{s}_{0}}}{l}=\frac{{{7,2.10}^{-2}}}{1,44}=0,05rad\]

Đáp án C

Câu 5: (Quốc gia – 2013) Hai con lắc đơn có chiều dài lần lượt là 81cm và 64cm được treo ở trần một căn phòng. Khi các vật nhỏ của hai con lắc đang ở vị trí cân bằng, đồng thời truyền cho chúng các vận tốc cùng hướng sao cho hai con lắc dao động điều hòa với cùng biên độ góc, trong hai mặt phẳng song song với nhau. Gọi Δt là khoảng thời gian ngắn nhất kể từ lúc truyền vận tốc đến lúc hai dây treo song song nhau. Giá trị Δt gần giá trị nào nhất sau đây:

A. 2,36s B. 8,12s C. 0,45s D. 7,20s

Hướng dẫn

Dạng phương trình dao động của hai con lắc đơn \[\alpha ={{\alpha }_{0}}\cos \left( \omega t-\frac{\pi }{2} \right)\]rad

Trong đó\[{{\omega }_{1}}=\sqrt{\frac{g}{{{l}_{1}}}}\]và \[{{\omega }_{2}}=\sqrt{\frac{g}{{{l}_{2}}}}\]\[\Rightarrow \frac{{{\omega }_{1}}}{{{\omega }_{2}}}=\sqrt{\frac{{{l}_{2}}}{{{l}_{1}}}}=\frac{8}{9}\Rightarrow {{\omega }_{1}}=\frac{8}{9}{{\omega }_{2}}\]

Điều kiện hai sợi dây song song \[\Leftrightarrow \]hai con lắc này có cùng li độ góc

Hệ nghiệm thứ nhất luôn cho nghiệm thời gian âm nên không có ý nghĩa vật lý

\[\Rightarrow t=\frac{36}{85}+\frac{72k}{85}\] thời gian ngắn nhất ứng với \[k=0\Rightarrow t=\frac{36}{85}s\]

Đáp án C

Câu 6:(Sở Bình Thuận – 2017) Để đo gia tốc trọng trường g tại một vị trí trên mặt đất ta có thể sử dụng con lắc đơn và

A. đo chu kì T, đo khối lượng m của con lắc, từ đó tính được gia tốc g.

B. đo chiều dài dây treo l, đo khối lượng m của con lắc, từ đó tính được gia tốc g.

C. đo biên độ A, đo chu kì T, từ đó tính được gia tốc g.

D. đo chiều dài dây treo l, đo chu kì T, từ đó tính được gia tốc g.

Hướng dẫn

Ta có thể đo gia tốc bằng cách sử dụng con lắc đơn, đo chu kì và chiều dài dây treo của con lắc sau đó tính gia tốc trọng trường từ biểu thức \[T=2\pi \sqrt{\frac{l}{g}}\]

Câu 7:(Chuyên Lê Hồng Phong – 2017) Tại một nơi có hai con lắc đơn dao động điều hòa. Trong cùng một khoảng thời gian, người ta thấy con lắc thứ nhất thực hiện được 4 dao động, con lắc thứ hai thực hiện được 5 dao động. Tổng chiều dài của hai con lắc là 164 cm. Chiều dài của mỗi con lắc là

A. \[{{l}_{1}}=100\]m, \[{{l}_{2}}=6,4\]m B. \[{{l}_{1}}=64\]cm, \[{{l}_{2}}=100\]cm

C. \[{{l}_{1}}=1\]m, \[{{l}_{2}}=64\]cm D. \[{{l}_{1}}=6,4\]cm, \[{{l}_{2}}=100\]cm

Hướng dẫn

\[T=\frac{\Delta t}{N}=2\pi \sqrt{\frac{l}{g}}\Rightarrow \frac{{{T}_{1}}}{{{T}_{2}}}=\frac{{{N}_{2}}}{{{N}_{1}}}=\sqrt{\frac{{{l}_{1}}}{{{l}_{2}}}}\Leftrightarrow \frac{{{l}_{1}}}{{{l}_{2}}}=\frac{25}{16}\]

Kết hợp với giả thuyết \[{{l}_{1}}+{{l}_{2}}=164\Rightarrow \]\[{{l}_{1}}=64cm\]và \[{{l}_{2}}=100cm\]

Đáp án B

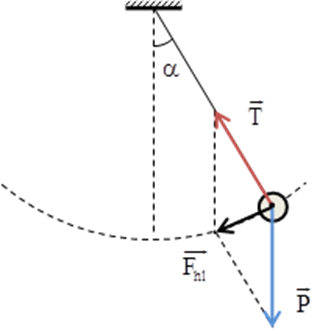
Câu 8:(THPT Thực hành – sp HCM – 2017) Một con lắc đơn gồm vật nặng có khối lượng m gắn với dây treo có chiều dài l. Từ vị trí cân bằng kéo lệch sợi dây sao cho góc lệch của sợi dây với phương thẳng đứng là \[{{\alpha }_{0}}={{60}^{0}}\] rồi thả nhẹ. Lấy \[g=10\]m/s². Bỏ qua mọi ma sát. Độ lớn của gia tốc khi lực căng dây có độ lớn bằng trọng lực

A. \[\frac{10}{3}\]m/s² B. 0 m/s² C. \[\frac{10\sqrt{5}}{3}\]m/s² D. \[\frac{10\sqrt{6}}{3}\]m/s²

Hướng dẫn

Biểu thức của lực căng dây \[T=mg\left( 3\cos \alpha -2\cos {{\alpha }_{0}} \right)\xrightarrow{T=P}\cos \alpha =\frac{1}{3}+\frac{2}{3}\cos {{\alpha }_{0}}=\frac{2}{3}\]

Gia tốc của vật

\[a=\sqrt{{{a}_{n}}+{{a}_{t}}}\] với a_n là gia tốc hướng tâm và a_t là gia tốc tiếp tuyến

\[{{a}_{t}}=\frac{{{F}_{hl}}}{m}=\frac{P\sin \alpha }{m}=g\sin \alpha \]

\[{{a}_{n}}=\frac{T-P\cos \alpha }{m}=g\left( 1-\cos \alpha \right)=\frac{g}{3}\]

Vậy

\[a=\sqrt{{{\left( \frac{g}{3} \right)}^{2}}+{{g}^{2}}{{\sin }^{2}}\alpha }=10\sqrt{\frac{1}{9}+\left( 1-{{\left( \frac{2}{3} \right)}^{2}} \right)}=\frac{10\sqrt{6}}{3}\] m/s²

Câu 9:(Chuyên Phan Bội Châu – 2017) Một con lắc đơn có chiều dài 40 cm, được treo tại nơi có gia tốc trọng trường bằng 10 m/s². Bỏ qua lực cản của không khí. Đưa dây treo lệch khỏi phương thẳng đứng một góc 0,15 rad rồi thả nhẹ. Tốc độ của quả nặng tại vị trí dây treo lệch khỏi phương thẳng đứng một góc 0,12 rad bằng

A. 6 cm/s B. 24 cm/s C. 18 cm/s D. 30 cm/s

Hướng dẫn

Tốc độ của vật năng tại vị trí có li độ góc α

\[v=\sqrt{gl\left( \alpha _{0}^{2}-{{\alpha }^{2}} \right)}=\sqrt{{{10.40.10}^{-2}}\left( {{0,15}^{2}}-{{0,12}^{2}} \right)}=18\]cm/s

Đáp án C

Câu 10:(Cẩm Lý – 2017)Tại một nơi trên mặt đất, con lắc đơn có chiều dài l₁ dao động với tần số 3 Hz, con lắc đơn có chiều dài l₂ dao động với tần số 4 Hz. Con lắc có chiều dài \[{{l}_{1}}+{{l}_{2}}\] sẽ dao động với tần số là

A. 1 Hz B. 5 Hz C. 2,4 Hz D. 7 Hz

Hướng dẫn

Ta có \[f\sim \frac{1}{\sqrt{l}}\xrightarrow{l={{l}_{1}}+{{l}_{2}}}\frac{1}{{{f}^{2}}}=\frac{1}{f_{1}^{2}}+\frac{1}{f_{2}^{2}}\Leftrightarrow \frac{1}{{{f}^{2}}}=\frac{1}{{{3}^{2}}}+\frac{1}{{{4}^{2}}}=2,4s\]

Đáp án C

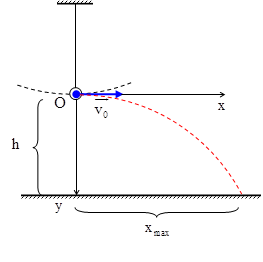
Câu 11:(Yên Lạc – 2017) Một con lắc đơn có chiều dài l m được treo dưới gầm cầu cách mặt nước 12 m. Con lắc đơn dao động điều hòa với biên độ góc \[{{\alpha }_{0}}=0,1\] rad. Khi vật đi qua vị tri cân bằng thì dây bị đứt. Khoảng cách cực đại ( tính theo phương ngang) từ điểm treo con lắc đến điểm mà vật nặng rơi trên mặt nước mà con lắc thể đạt được là.

A. 49 cm B. 95 cm C. 65 cm D. 85 cm

Hướng dẫn

+ Tốc độ của con lắc khi đi qua vị trí cân bằng

\[{{v}_{0}}=\sqrt{gl}{{\alpha }_{0}}=\sqrt{10.1}.0,1=0,1\pi \]m/s

+ Thời gian chuyển động của vật \[t=\sqrt{\frac{2h}{g}}=\sqrt{\frac{2.12}{10}}=1,5s\]

+ Tầm xa của vật

\[{{x}_{max}}={{v}_{0}}t=0,1\pi .1,5=49cm\]

Đáp án A

Câu 12:(Chuyên Lê Quý Đôn – 2017) Hai con lắc đơn có khối lượng như nhau, cùng dao động điều hòa với biên độ nhỏ trong hai mặt phẳng thẳng đứng song song nhau. Biết chu kì con lắc thứ nhất gấp 2 lần chu kì con lắc thứ hai, biên độ của con lắc thứ hai gấp 3 lần biên độ của con lắc thứ nhất. Chọn mốc thế năng của mỗi con lắc ở vị trí cân bằng của chúng. Tại một thời điểm nào đó, hai con lắc có cùng li độ, đồng thời động năng con lắc thứ nhất gấp 3 lần thế năng của nó. Tỉ số giữa tốc độ của con lắc thứ hai và con lắc thứ nhất tại thời điểm đó bằng

A. \[\frac{140}{3}\] B. \[\frac{35}{3}\] C. \[\sqrt{\frac{35}{3}}\] D. \[\sqrt{\frac{140}{3}}\]

Hướng dẫn

Ta có \[{{T}_{1}}=2{{T}_{2}}\Rightarrow {{\omega }_{2}}=2{{\omega }_{1}}\]

Khi hai con lắc này gặp nhau \[{{s}_{1}}={{s}_{2}}=\frac{{{s}_{01}}}{2}\]

\[\left| \frac{{{v}_{02}}}{{{v}_{01}}} \right|=\frac{{{\omega }_{2}}\sqrt{s_{01}^{2}-{{s}_{1}}}}{{{\omega }_{2}}\sqrt{s_{02}^{2}-{{s}_{2}}}}\xrightarrow{{{s}_{02}}=3{{s}_{01}}}\left| \frac{{{v}_{02}}}{{{v}_{01}}} \right|=\frac{{{\omega }_{2}}\sqrt{s_{01}^{2}-{{\left( \frac{{{s}_{01}}}{2} \right)}^{2}}}}{{{\omega }_{2}}\sqrt{9s_{01}^{2}-{{\left( \frac{{{s}_{01}}}{2} \right)}^{2}}}}=\sqrt{\frac{140}{3}}\]