Bài Tập Trắc Nghiệm Số Phức

Câu 1. Điểm nào trong các điểm sau đây là điểm biểu diễn hình học của z= -5+ 4i trong mặt phẳng tọa độ Oxy:

A.(-5; 4) B. C(5; -4) C.B(4;-5) D. D(4; 5)

Câu 2. Cho hai số phức z = 1+2i và w = 3- i . Tính tổng của 2 số phức w và z.

A. 4+ i B.4 – i C. 4 – 3i D. 4 + 3i

Câu 3. Định tất cả các số thực m để phương trình − 2z + 1 − m = 0 có nghiệm phức z thỏa mãn |z| = 2.

A. m = −3. B m = −3; m = 9. C. m = 1; m = 9. D m = −3; m = 1; m = 9.

Câu 4: Số phức liên hợp của z = 2016 + 2017i là số phức nào?

A −2016 − 2017i. B −2016 + 2017i. C. 2017 − 2016i. D 2016 − 2017i.

Câu 5: Phần thực và phần ảo của số phức z = 1+2i lần lượt là

A 2 và 1. B 1 và 2i. C 1 và 2. D 1 và i.

Câu 6: Cho số phức z = −3 + 4i. Gọi M là điểm biểu diễn số phức liên hợp. Tung độ của điểm M là

6. B. 4. C. −4. D. −6.

Câu 7: Tìm phần ảo của số phức z = 5 − 8i.

A. 8. B. −8i. C 5. D. −8.

Câu 8: Cho số phức z = 5 − 4i. Môđun của số phức z bằng

A. 3. B. 9. C. √ 41. D. 1.

Câu 9: Cho số phức z = 2018 − 2017i. Điểm M biểu diễn của số phức liên hợp của z là

A. M(−2018; 2017). B. M(2018; −2017). C. M(−2018; −2017). D. M(2018; 2017).

Câu 10: Cho số phức z thỏa mãn (3 + 2i)z + = 4 + i. Hiệu phần thực và phần ảo của số phức z là

A. 3. B. 2. C 1. D. 0.

Câu 11: Cho số phức z = (1 + 3i)(4 − i), phần thực của z bằng bao nhiêu?

A. 4. B. 1. C. 11. D. 7.

Câu 12: Cho số phức z = (1 + 2i)(5 − i), z có phần thực là

A. 5. B. 3. C. 9. D. 7.

Câu 13: Trong mặt phẳng phức, gọi A, B, C, D lần lượt là các điểm biểu diễn các số phức

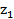= −1 + i, = 1 + 2i, 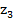= 2 − i, 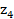= −3i. Gọi S diện tích tứ giác ABCD. Tính S.

A. S = . B. S = 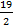. C. S = 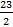. D. S = .

Câu 14: Cho hai số thực x, y thỏa mãn phương trình x + 2i = 3 + 4yi. Khi đó giá trị của x, y là:

A. x = 3, y = 2. B x = 3i, y = . C x = 3, y = . D x = 3, y = − .

Câu 15: Tìm tọa độ điểm biểu diễn của số phức z = (2 - 3i)(4 - i) 3+2i trên mặt phẳng Oxy.

A. (−1; −4). B. (1; 4). C. (1; −4). D. (−1; 4).

Câu 16: Tập hợp điểm biểu diễn số phức z thỏa mãn 2|z−1| = |z + ¯z + 2| trên mặt phẳng tọa độ là một:

đường thẳng. B. đường tròn. C. parabol. D. hypebol.

Câu 17: Tính mô-đun số phức nghịch đảo của số phức z =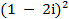

A. 1 √ 5 . B. √ 5. C. 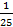D. .

Câu 18: Tổng các nghiệm phức của phương trình 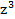+ 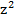−2 = 0 là

A. 1. B. −1. C. 1 − i. D. 1 + i.

Câu 19: Tìm phần thực và phần ảo của số phức z = 1 − πi.

A. Phần thực là 1 và phần ảo là −π. B. Phần thực là 1 và phần ảo là π.

C. Phần thực là 1 và phần ảo là −πi. D. Phần thực là −1 và phần ảo là –π

Câu 20: Điểm biểu diễn của các số phức z = 7 +bi với b ∈ R nằm trên đường thẳng có phương trình là:

A. y = 7. B. x = 7. C. y = x + 7. D. y = x.

Câu 21: Cho số phức z, biết rằng các điểm biểu diễn hình học của các số phức z; iz và z + iz tạo thành một tam giác có diện tích bằng 18. Tính mô-đun của số phức z.

A. 2 √ 3. B. 3 √ 2. C 6. D. 9.

Câu 22: Tìm tất cả các nghiệm của phương trình 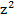+2z +5 = 0.

A. 1 + 2i; 1 − 2i. B. 1 + i; 1 − i. C. −1 + 2i; −1 − 2i. D. −1 + i; −1 − i.

Câu 23: Cho số phức z thỏa mãn |z−2+3i|+|z+2+i| = 4√ 5. Tính giá trị lớn nhất của

P = |z − 4 + 4i|.

A. max P = 4√ 5. B. max P = 7√ 5. C. max P = 5√ 5. D. max P = 6√ 5.

Câu 24: Tìm m để số phức z = 2m + (m − 1)i là số thuần ảo.

A. m = − 1. B. m = − 2 . C. m = 0. D. m = 1.

Câu 25: . Tập hợp tất cả các điểm biểu diễn cho số phức z trong mặt phẳng phức thỏa mãn điều kiện |z − i| = |z + i| là:

A. một đường thẳng. B. một đường tròn. C. một đường elip. D. một đoạn thẳng.

Câu 26: Tìm giá trị lớn nhất của P = |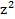 − z| + | 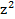+ z + 1| với z là số phức thỏa mãn

|z| = 1.

A. √ 3. B. 3. C. . D. 5.

Câu 27: Cho số phức z = −3 + 4i. Gọi M là điểm biểu diễn số phức z. Tung độ của điểm M là:

A. 6. B. 4. C. −4. D. −6.

Câu 28: Cho 4 điểm M, N, P, Q là các điểm trong mặt phẳng phức theo thứ tự biểu diễn các số −i, 2 + i, 5, 1 + 4i. Hỏi điểm nào là trọng tâm của tam giác tạo bởi ba điểm còn lại?

A. M. B. N. C. P. D. Q.

Câu 29: Cho hai số phức 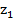= −1 + 2i, = −1 − 2i. Giá trị của biểu thức 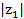² + |z₂|² bằng: